2022-06-03 東京大学
発表者
西出 亮介(東京大学 大学院総合文化研究科 広域科学専攻 博士課程2年)
石原 秀至(東京大学 大学院総合文化研究科 広域科学専攻 准教授/東京大学 生物普遍性連携研究機構 准教授)
発表のポイント
- 平面上では止まったパターンが得られる条件でも、曲面上では伝播するパターンになることを発見した。
- 曲面の曲率(注1)によりパターンが伝播するという、曲率のもたらす新規な伝播機構を明らかにした。
- 曲率によるパターン伝播は、生体内や起伏のある地表上での植生分布など、曲面上で見られる様々なパターンに生じ得るため、幅広い分野への応用が期待される。
発表概要
魚の体表模様や植生パターン、感染者数の空間的な広がりなどは、数理的には時空間的なパターンとして捉えることができ、数式を用いてパターンの振る舞いを理解し、応用するための研究が多くなされています。パターンは様々な場所で現れますが、どこで現れるかによって、パターンの形や振る舞いが変わってきます。近年、曲面上に現れるパターンに対して、曲面の形状やその曲率がどのような影響・効果をもたらすのかについて関心がもたれ、様々な理解が進んできていますが、未だ多くのことがわかっていません。特に生体では、体や器官、細胞が複雑な形状をしており、その表面である曲面の上で細胞集団運動やタンパク質分布がパターンとして観察され、生体機能とも密接に関係するため、パターンが曲面上でどのように振る舞うのかを理解することは重要です。
東京大学大学院総合文化研究科広域科学専攻の西出亮介大学院生、同専攻および同大学生物普遍性連携研究機構の石原秀至准教授らの研究グループは、理論的解析と数値シミュレーションにより、平面上で静止するパターンが曲面上では一方向に伝わっていく(伝播する)ことを発見しました。パターンの伝播現象は、神経パルスの伝達や生態系における種の侵入などで知られていましたが、本研究で明らかにされた伝播現象は曲面上だけで起こり、これまで知られている伝播パターンとは異なる新しい機構で生じていることがわかりました。
本研究成果によって、曲面がパターンの振る舞いに与える影響・効果に対する理解を深めました。また、曲面上のパターンは様々な場所に現れるため、生物が曲面形状を伝播制御機構として使用している可能性が考えられるなど、他分野における研究、応用へと発展していくことが期待されます。
本研究成果は、2022年6月2日(米国東部夏時間)に国際科学誌「Physical Review Letters」に掲載されました。
発表詳細
研究背景
魚の体表模様や地表に現れる植生パターン、骨組織上の細胞集団のように、パターンが曲面の上で観察されることがしばしばあります。近年の研究により、曲面の空間構造がパターンの決定に重要な因子であることがわかってきました。例えば、パターンの位置や形状が曲面形状に応じて変調を受けること、曲率によってパターンの分裂が起こることなどが報告されています。また、生命科学分野では、微細加工技術や観察技術の発展もあり、曲面の形状が細胞集団や遺伝子発現に影響を与えるなど、曲面の効果や役割が明らかになってきています。曲面とパターンダイナミクスの関係を理解することで、現象の理解を深め、曲面形状を用いたパターン制御機構などの応用へとつながります。しかし、曲面がパターンやそのダイナミクスに与える影響の理解は未だ発展途上と言えます。
研究内容
曲面とパターンダイナミクスの関係を調べるため、曲面上でTuringパターン(注2)を数値シミュレーションにより調べました。Turingパターンとは、分子の拡散と化学反応によって現れる、数理的にも最もよく知られているパターン形成メカニズムの一つで、平面上では、ストライプやドット状の静止したパターンを形成します。Turingパターンを曲面上で調べたところ、平面では静止していたパターンが、ある特定の曲面上で伝播するということを発見しました(図1)。これは、曲面の曲率によってパターン伝播現象が引き起こされることを意味します。これまでにも曲面上でTuringパターンを調べる研究はありましたが、そこでは静止したパターンが得られることが前提となっており、曲面上でのパターン伝播は過去の知見とは異なる新規な結果です。
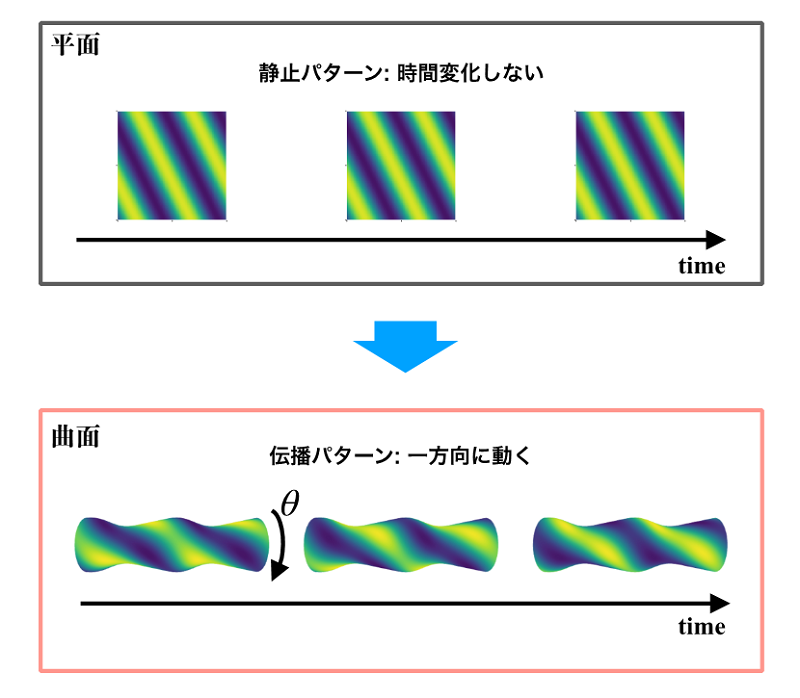
図1:曲率によるパターン伝播。平面では静止したTuringパターン(上)が得られるが、曲面上では伝播するパターン(下)が得られた。
この伝播現象を理解するために、軸対称曲面(注3)の場合に数値シミュレーションと理論的な解析を行いました。数値シミュレーションからは、「曲面の対称性」と「パターンの対称性」に依存してパターンの伝播が起こることがわかりました(図2)。この結果について理論的な解析を行い、Turingパターンを含む反応拡散系(注4)一般に対して、伝播が起こる必要条件を導きました。本研究グループが見つけたパターンの伝播現象は曲面上だけで起こり、これまで知られている伝播パターンとは異なる新しい機構で生じていることがわかりました。
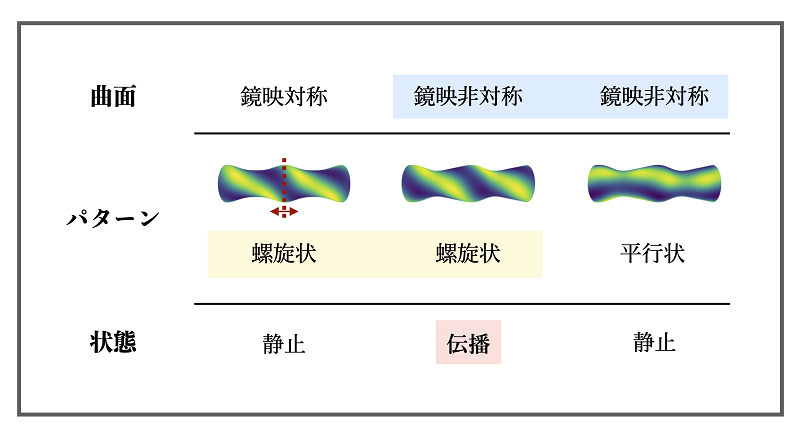
図2:パターン伝播と、曲面の対称性とパターンの対称性との関係。曲面がx=0(赤点線)で折り返して一致する鏡映対称性がなく、パターンが螺旋状の場合にはパターンが伝播する。
社会的意義・今後の予定
本研究により、曲率がパターンを伝播させる効果を持つことを示しました。反応拡散系は物理・化学・生物学を含む様々な分野で数理モデルとして使われており、パターンは曲面上で豊富に見られることから、幅広い分野に対して、この伝播現象が観察されるだろうと期待されます。例えば、生物学的文脈では、生体内の器官を形成する際に空間の位置を検知する機構として使われている可能性が考えられます。また、伝播現象が曲面の対称性と関わっていることから、曲面を制御することにより伝播を調整するような応用が期待されます。
本研究は、科研費「生体組織の成長を理解するための新規力学モデルの発展と応用(JP18H01185)」、「JST CREST 細胞動態スペクトラムから紐解く多細胞秩序の創発規則(JPMJCR1923)」「JST SPRING グリーントランスフォーメーション(GX)を先導する高度人材育成(JPMJSP2108)」の支援により実施されました。
問い合わせ先
東京大学 大学院総合文化研究科 広域科学専攻 相関基礎科学系
准教授 石原 秀至(いしはら しゅうじ)
用語解説
(注1)曲率:
曲面が、どのくらい曲がっているかを定量的に表す指標。
(注2)Turingパターン:
数学者Alan Turingの提案した方程式系により作られるパターンで、対応する化学反応も実際に観察されている。魚の体表模様やマウスの指の形成過程のような生物学的なパターンを数式で説明する際にも現れる。その数理的な機構の一般性もあって、様々な分野にまたがって多くの研究がなされている。
(注3)軸対称曲面:
パターンや曲面に対して「ある面で折り返す」、「並進させる」などの操作を施しても、元の形が変わらない場合、そのパターンや曲面はその操作に対応した対称性を持つと言う。軸対称曲面は、ある軸の周りに回転させても形が変わらない曲面のこと。
(注4)反応拡散系:
化学成分の濃度や密度の分布が、反応と拡散により時間発展する系。相分離、神経パルスの伝播、感染症などのモデルとして用いられており、Turingパターンも反応拡散系において現れるパターンの一つである。
論文情報
西出亮介*, 石原秀至 , “Pattern Propagation Driven by Surface Curvature,” Physical Review Letters: 2022年6月2日, doi:10.1103/PhysRevLett.128.224101.
論文へのリンク (掲載誌)