「安定分布」と「キュービック則」による統一的な特徴付けに成功
2020-01-24 京都大学
梅野健 情報学研究科教授、柿中晋治 同修士課程学生らの研究グループは、暗号通貨市場の価格変動が「安定分布」と「キュービック則」という二つの統計則(べき則)によって統一的な特徴付けがされることを発見しました。
暗号通貨などの激しい価格変動をする通貨の特徴付けは「安定分布」か「キュービック則」かで論争がありました。本研究グループは、価格変動データのフーリエ変換によって分布の裾野部分の特徴を正確に求めることにより、価格変動の分布全体においては、対称的な安定分布に従い、分布の裾(テイル)の部分ではべき指数3のべき則(キュービック則)に従うことを突き止めました。またこの結果は、2年前に本研究グループが発見した「べき則」の根拠を説明する「超一般化中心極限定理」が暗号通貨の世界でも成立することを示唆する結果となります。
これらの結果を基に、暗号通貨市場の持つ正確なリスクの定量的な評価につながることが期待されます。
本研究成果は、2020年1月24日に、国際学術誌「Journal of the Physical Society of Japan」のオンライン版に掲載されました。
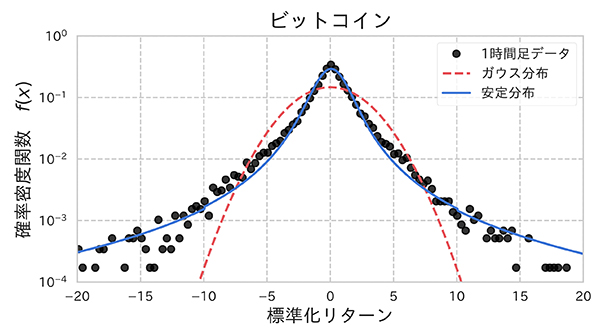
図:2017年1月1日-2019年1月1日のビットコインの価格変動(時間変動幅Δt=1時間)の対数収益率の分布
詳しい研究内容について
暗号通貨のビッグデータが持つ普遍的な統計則を発見
―「安定分布」と「キュービック則」による統一的な特徴付けに成功―
概要
京都大学大学院情報学研究科 梅野健 教授、柿中晋治 同修士課程学生らの研究グループは、暗号通貨市場の価格変動が「安定分布」と「キュービック則」という二つの統計則(べき則)によって統一的な特徴づけがされることを発見しました。
暗号通貨などの激しい価格変動をする通貨の特徴付けは「安定分布」か「キュービック則」かで論争がありました。本研究グループは、価格変動データのフーリエ変換によって分布の裾野部分の特徴を正確に求めることにより、価格変動の分布全体においては、対称的な安定分布に従い、分布の裾(テイル)の部分ではべき指数 3 のべき則(キュービック則)に従うことを突き止めました。
またこの結果は、2年前に本研究グループが発見した「べき則」の根拠を説明する「超一般化中心極限定理」が暗号通貨の世界でも成立することを示唆する結果となります。これらの結果を基に、暗号通貨市場の持つ正確なリスクの定量的な評価につながることが期待されます。
本研究成果は、2020 年 1 月 24 日に日本物理学会の国際学術誌「Journal of the Physical Society of Japan」にオンライン掲載されました。
1.背景
ブロックチェーンの暗号技術で作られた新しい暗号通貨は、近年世界中で取引量が増加していますが、その価格変動が激しいために、価格変動の統計的特徴付けを明らかにすることが課題でした。その論点は、通常の為替変動と暗号通貨の価格変動が同じなのか異なるのか、あるいは価格変動の分布がどの様な分布に従ってい
るかどうかです。特に後者に対しては、「キュービック則」という「「べき則」に従うか、「安定分布」という「「べき則」に従うかについて2つのグループの結果が分かれており、果たして両者のどちらが正しいのか未解明で
した。本研究プロジェクトは、データのエルゴード性を用いて梅野教授が福永匠(2016 年 4 月-2018 年 3 月京都大学大学院情報学研究科修士課程学生)と共に、価格データの対数収益率から特性関数を計算して安定分布を正確にパラメータ推定する方法を独自に開発した(Fukunaga, Umeno, arzXiv: 1709.06279v2., 2018) 2016年春頃に、全ての金融市場の価格変動の特徴付けを行うため自発的に発足しました。
2.研究手法・成果
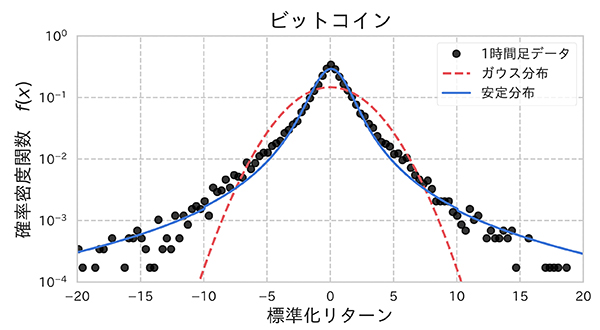
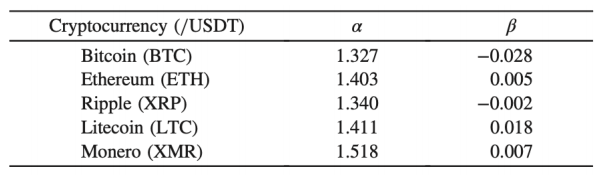
手法としては、まず価格変動の対数収益率データに対して、特性関数(確率密度関数のフーリエ変換)を正確に求め、安定分布とのパラメータフィッティングを行います。その結果、暗号通貨の種類によらずに、安定分布のパラメータがα=1.3〜1.5, βが 0 近傍のほぼ対称の安定分布で特徴づけられることが解りました。これは安定分布のパラメータが、α=2,「 β=0 に相当するガウス分布とは明らかに異なる、裾野(テイル)が厚いいわゆるファットテイル性を持つ分布であることがはっきりとしました(図 1 参照)。
表 1:「 安定分布(α、β)による暗号通貨の推定値(2017/01/01〜2019/01/01 のデータを使用)
また、本手法による特徴付けがどの程度正確かを定量的に測るために、分布間の距離の指標を考案しました。この指標を用いて分布全体で見たところ、先行研(Begusic,et.al.2018)で言われていたキュービック則よりも安定分布の方が近いことも、定量的に明らかにしました。また一方、分布の裾の部分においては、データの分布と安定分布とが完全に一致している訳ではなく、尤度比検定(Clauset,2009)を用いることにより、分布の裾の部分は「キュービック則」の方がより良い分布であることを実証しました(図2参照)。
これらの結果より、分布全体で見ると安定分布タイプの「べき則」の記述が正確であり、分布を裾の部分を見ると「キュービック則」タイプの「べき則」が正確であり、これらの結果は暗号通貨の種類によらずに普遍的に成立することが解りました。安定分布タイプのべき則があらわれる理由として、グループが 2018 年に発見した超一般化中心極限定理があげられます。
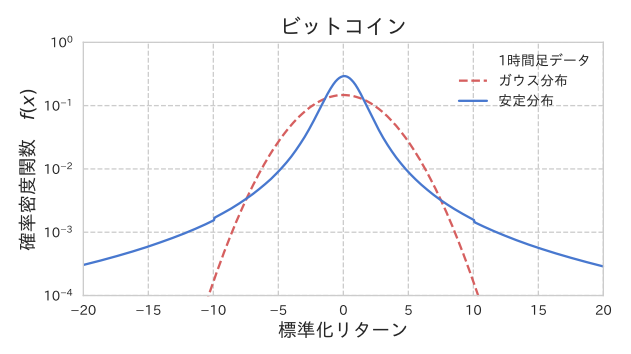
図 1: 2017/01/01-2019/01/01 のビットコインの価格変動(時間変動幅 Δt=1 時間)の対数収益率の分布。 赤色の破線が、データと同じ平均値と分散を持つガウス分布との比較。
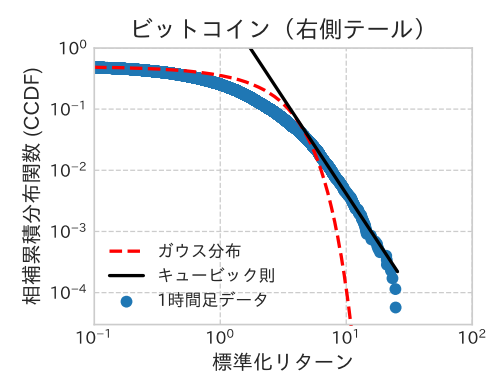
図 2: 2017/01/01-2019/01/01 のビットコインの価格変動(時間変動幅 Δt=1 時間)の相補累積分布関数とキュービック則との比較。赤色の破線が、データと同じ平均値と分散を持つガウス分布との比較。
3.波及効果、今後の予定
暗号通貨市場の定量的なリスク評価につながるリスク指標を、今回明らかにした暗号通貨の価格変動の統計モデルを基礎に構築していきます。また暗号通貨に限らず、他の金融市場との比較を行うことにより、暗号通貨市場の特徴付けを行いたいと考えます。また、暗号通貨の定量的なリスク評価、暗号通貨市場の安定性を評価すると共に、裾野部分では安定分布ではなく何故「「キュービック則」が普遍的にあわわれるのか、という残された数理的課題の解明を行っていく予定です。
<参考リンク>
[1]「 京都大学発表「なぜ世界は「べき則」で表されるのかービッグデータの新しい統計法則の発見―
(2018 年 4 月)http://www.kyotou.ac.jp/ja/research/research_results/2017/180402_1.html
<用語解説>
べき則: 確率分布が、正規分布(ガウス分布)の様に、変動幅に対して指数関数的にゼロに減衰するのではなく、変動幅に対してべき的にゆっくりゼロに減衰すること。確率密度関数を数式で表現すると、以下の様になります。ここで α が、べき指数となります。
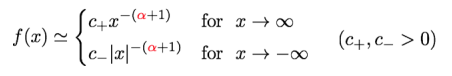
キュービック則:片側べき則で、べき指数がα=3 に相当する確率分布。
安定分布:正規分布(ガウス分布, 指数α=2)やコーシー分布(べき指数α=1,「 β=0)を含むべき指数α(0<α≦2), 歪度β(-1≦β≦1)のパラメータを持つ確率分布であり、独立同分布に従う確率変数の和の極限を適当にスケール変換すると、その極限分布は安定分布になることが知られています(一般化中心極限定理)。
対数収益率:ある2つの時刻の価格の比を収益率と定義し、その対数をとったもの。
尤度比検定:実データが与えられたとしても、それがある分布に厳密に従うことを証明することは困難なことです。それに対して、2種類の分布(統計モデル)を考え、そのどちらがもっともらしいかを尤度比を用いて検定することは実行可能であり、この尤度比を用いる統計学的検定法を尤度比検定といいます。
<研究者のコメント>
暗号通貨は、研究を始めた当初(2016 年頃)はいきなり暴騰して暴落する「怪しい通貨」でした。しかし、ジュネーブ国際空港では暗号通貨の価格が他の主要通貨と共に表示されるなど、現在では決して「「仮想通貨」などではなく、実体として国際的な通貨となりつつあります。この暗号通貨の価格変動の持つ不思議な性質やその普遍性の一端を明らかにし、暗号通貨の本質を理解するデータサイエンスとしての魅力が皆さんに伝われば幸いです。
<論文タイトルと著者>
タイトル:Characterizing ryptocurrency Market with Levy’s Stable Distributions
(レビ安定分布による暗号通貨市場の特徴付け)
著 者: Shinji Kakinaka and Ken Umeno
掲 載 誌 :Journal of the Physical Society of Japan(Vol.89 No.2 Article ID 024802)
D O I: 10.7566/JPSJ.89.024802