電力ネットワークの同期は対称性がカギ

再エネ普及時の安定供給につながる、世界初の理論解明

2018-04-27　東京工業大学　科学技術振興機構（ＪＳＴ）

ポイント

電力の安定供給に欠かせない、電力ネットワークの発電機群の同期現象を世界で初めて理論解明。
ネットワークの対称性が発電機群を同期させることを証明し、電力ネットワークの集約モデルを構築。発電機群の振る舞いの効率的解析、制御系の最適設計が可能に。
再生可能エネルギーの大量導入にも耐えうる電力網設計への発展に期待。

東京工業大学工学院システム制御系の石崎孝幸　助教と井村順一　教授は、ノースカロライナ州立大学のＮＳＦ　ＥＲＣ　ＦＲＥＥＤＭシステムセンター注１）のアラーニャ・チャクラボッティ　准教授との共同研究で、電力ネットワークのモデリング・解析・制御に関する一連の研究成果をグラフ理論注２）で検討し、ネットワーク結合された発電機群の同期注３）を実現するための基本原理を明らかにしました。そしてこの原理に基づき、送電網で複雑に結合された発電機群の振る舞い（回転子の位相角や連結点の電圧値など）を効率的に解析・制御できる、電力ネットワークの集約モデル注４）を構築する手法を世界に先駆けて開発しました。

日本では太陽光発電など再生可能エネルギーによる発電の大量導入が見込まれています。これに伴う課題として、再生可能エネルギーは、天候や気候といった気象条件の変化で発電量が不規則に変動するため、電力系統に組み込まれた際に、電力供給の安定性を損なうと考えられてきました。

発電機群の回転子の位相角が揃う「同期現象」の解析は、電力の安定供給を実現するために不可欠です。再生可能エネルギーの普及が進むと、火力発電など従来型発電機群の同期現象を詳細に解析する必要性はますます高まると予想されます。しかし、これまでの発電機群の同期現象の解析は、数値シミュレーションによるものが主流でした。理想的な送電ネットワークと発電機群の正確な同期について、その原理を理論的に明らかにした研究は、今回が世界初といえます。

本研究では、グラフ理論におけるネットワークの対称性（グラフの自己同型性）注５）が発電機群の同期を特徴づけることを理論的に証明しました。さらに、この送電網の解析に基づき、オームの法則やキルヒホッフの法則注６）などの物理法則に従う電力ネットワークの集約モデルの構築手法を開発しました。

本成果は、再生可能エネルギーの送電網への大量導入によりさらなる複雑化が予想される将来の電力システムに対応し、電力を安定供給するための解析・制御手法を開発する基盤として、その発展が期待されます。

本研究成果は、平成３０年４月２６日（日本時間）に米国電気電子学会誌「Ｐｒｏｃｅｅｄｉｎｇｓ　ｏｆ　ｔｈｅ　ＩＥＥＥ」のオンライン速報版で公開されました。

本成果は、以下の事業・研究領域・研究課題によって得られました。

科学技術振興機構戦略的創造研究推進事業チーム型研究（ＣＲＥＳＴ）

研究領域	「分散協調型エネルギー管理システム構築のための理論及び基盤技術の創出と融合展開」（研究総括：東京工業大学工学院　教授　藤田政之）
研究課題名	「太陽光発電予測に基づく調和型電力系統制御のためのシステム理論構築」
代表研究者	東京工業大学工学院　教授　井村順一
研究実施場所	東京工業大学
研究開発期間	平成２７年４月～平成３２年３月

＜背景＞

火力発電所など複数の発電機群の回転子の位相角が揃う「同期現象」は、電力の安定供給に深く関係することが知られています。具体的には、ある発電機が同期しなくなると、その発電機や周辺の発電機は安定に運転することができなくなり、最悪の場合、停電などの重大な事象が引き起こされます。このような観点から、電力システムにおける発電機群の同期現象の解析は非常に重要でした。

特に今後、太陽光発電など再生可能エネルギーの大量導入を見据える日本においては、効率的な発電・送電に関わる同期現象の解析の必要性はこれまで以上に高まることが予想されます。再生可能エネルギーは、天候や気候といった気象条件の変化によって発電量が不規則に変動してしまい、発電機群の同期を維持することがより難しくなると予想されるためです。

発電機群の同期現象の解析は従来、数値シミュレーションに基づくアプローチが主流でした。どのような送電ネットワークを構築すれば発電機群が適切に同期するか、その原理を理論的に明らかにした研究はこれまでにありませんでした。

＜研究成果＞

本研究では、電力ネットワークのモデリングや安定性解析、安定化制御などに関する一連の研究成果を、グラフ理論という数学理論の観点から検討しました。グラフとは、頂点と辺で構成されるネットワーク構造の概念です。これを電力ネットワークに当てはめると、連結点はグラフの頂点として、連結点の間を結ぶ送電線はグラフの辺として表現できます。解析の結果、グラフ理論におけるネットワークの対称性が、送電網と一体となった（ネットワーク結合した）火力発電所の発電機群の同期を実現する基本原理であることを明らかにしました。

さらに、この基本原理に基づき、複雑にネットワーク結合された発電機群の振る舞い（回転子の位相角や連結点の電圧値など）を効率的に解析・制御するための新たな電力ネットワークの集約モデルの構築手法を世界に先駆けて開発しました。

送電網でネットワーク結合された発電機の振る舞いは、微分方程式と代数方程式をまとめた複雑な方程式（微分代数方程式）により表現されます。このうち、微分方程式はニュートンの運動の第２法則から導かれる“発電機の時間変化”を表現し、代数方程式はオームの法則やキルヒホッフの法則から導かれる“送電網の連結点における電力バランス”を表現します。

この微分代数方程式の解析は、Ｋｒｏｎ縮約（Ｋｒｏｎ　Ｒｅｄｕｃｔｉｏｎ）と呼ばれる簡略化手法によって、数学的に等価な微分方程式モデル（Ｋｒｏｎ縮約モデル）に変形して行われることが一般的でした。しかし、このような既存のアプローチでは、連結点の電圧を表す変数を削除することにより、送電網を表す代数方程式を消去してしまいます。すなわち、Ｋｒｏｎ縮約モデルは、オームの法則やキルヒホッフの法則などの物理法則を反映した送電網のネットワーク構造が直接的には見えない形式で表現されてしまいます。このため、既存のアプローチは、送電網のネットワーク構造と発電機群の同期現象の関係を解析するのに不向きでした。

これに対して、本研究ではグラフ理論に基づき、代数方程式に含まれる送電網のネットワーク構造を対称性の観点から解析しました。代数方程式を消去しないで、送電網の連結点の電圧の同期にも着目して発電機の振る舞いを解析した結果、送電網の対称性（図１）が発電機群の同期を実現する基本原理であることを明らかにしました。

さらに、同期している発電機群とそれらを結合する送電網を同時に集約するという新たな着想を加え、数学的にも物理的にも妥当な集約モデルを構築できました（図２）。従来の集約モデルは連結点の電圧変数が消去されたＫｒｏｎ縮約モデルから構築されていたため、現実の電力ネットワークにおいて成り立つ物理法則が反映されていませんでした。本成果は、これまで数学寄りの観点から研究されてきた集約という概念を、電力ネットワークという物理システムにいかに適用すべきかを真に考えることよって実現されたといえます。

＜今後の展開＞

本成果は、大規模で複雑な電力システムに対応し、電力の安定供給を実現するための解析・制御手法を開発する基盤として、その発展が期待されます。

今後は、コンバーターなどを含めたより複雑な電力システムへの展開や、発電機群の同期現象を近似的に解析する理論の構築を目指します。

＜参考図＞

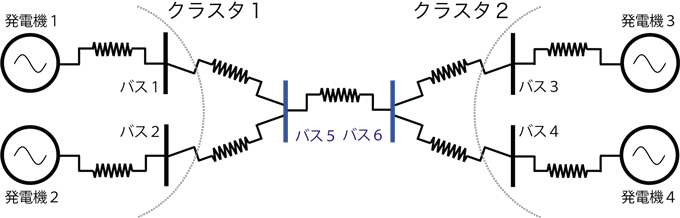
図１　バス（連結点）に関して対称な電力ネットワーク例

４つの発電機と６つのバス（連結点）で構成される電力ネットワーク。発電機１と２およびそれらが連結するバス１と２はバス５に関して対称なネットワークとなっている。同様に、発電機３と４およびバス３と４はバス６に関して対称となっている。２組の対称な発電機群とバス群がクラスタ１と２として示されている。

図２　集約された電力ネットワーク

図１における２組の対称な発電機群とバス（連結点）群をクラスタとして同時に集約することによって得られる集約モデル。オームの法則やキルヒホッフの法則に従い、数学的にも物理的にも妥当な集約モデルとなっている。なお、従来の集約モデルは連結点の電圧変数を消去したＫｒｏｎ縮約モデルから構築されており、現実の電力ネットワークにおいて成り立っている物理法則が反映されていなかった。

＜用語解説＞

注１）ＮＳＦ　ＥＲＣ　ＦＲＥＥＤＭシステムセンター: ノースカロライナ州立大学に本部を置く、全米エネルギー技術開発リサーチセンター。米国国立科学財団（ＮＳＦ）が実施する工学研究センター（ＥＲＣ）の１つ。再生可能電気エネルギーの未来の供給・管理システム（Ｆｕｔｕｒｅ　Ｒｅｎｅｗａｂｌｅ　Ｅｌｅｃｔｒｉｃ　Ｅｎｅｒｇｙ　Ｄｅｌｉｖｅｒｙ　ａｎｄ　Ｍａｎａｇｅｍｅｎｔ　Ｓｙｓｔｅｍｓ）に関する研究を行っている。
注２）グラフ理論: 頂点（ノード）の集合と辺（エッジ）の集合で構成されるグラフ（ネットワーク構造）に関する数学の理論。送電網のネットワークは、連結点が頂点であり、連結点の間を結ぶ送電線が辺であるようなグラフとして解釈される。
注３）発電機群の同期: 複数の発電機のタービンなどの回転子の位相角が同じ、もしくは十分に近いこと。各回転子は特定の周波数（日本では５０ヘルツまたは６０ヘルツ）を基準として、その周波数を維持するように回転している。各発電機の周波数の差が位相角の差を生む。
注４）電力ネットワークの集約モデル: 冗長な変数を集約する（１つにまとめて表現する）ことにより得られる、電力ネットワークの縮約された微分代数方程式モデル。ネットワーク結合された発電機の振る舞いは、微分方程式と代数方程式をまとめた複雑な微分代数方程式により表現される。それらの方程式の変数は各発電機の回転子の位相角や連結点の電圧値を表しており、大規模な電力ネットワークの振る舞いを記述するためには一般に多くの変数を必要とする。従って、効率的な解析のために、電力ネットワークの振る舞いへの影響が小さい冗長な変数の削減がしばしば行われる。
注５）ネットワークの対称性（グラフの自己同型性）: グラフの頂点の配置位置の入れ換えに関してグラフ構造が不変であることにより定義されたグラフの対称性の概念。
注６）オームの法則、キルヒホッフの法則: 電気回路における電圧や電流などの物理量の関係を表す物理法則。オームの法則は、回路内のある２点間の電圧差がその間を流れる電流に比例することを表す。キルヒホッフの法則は、回路内の分岐点において、その点に流入する電流の和がその点から流出する電流の和に等しいことを表す。