2018/08/22 理化学研究所
理化学研究所(理研)計算科学研究センター量子系物質科学研究チームのサンドロ・ソレラ客員主管研究員、関和弘客員研究員、白川知功客員研究員、柚木清司チームリーダーと創発物性科学研究センター計算量子物性研究チームの宮腰祥平特別研究員らの国際共同研究グループ※は、「グラフェン[1]」を等方的に引っ張ったとき、その原子構造と電子状態がどのように変わるかをシミュレーションにより解析し、従来の予想とは異なる新しいシナリオを発見しました。
本研究成果は、グラフェンの基礎物性の新たな発見であるだけでなく、グラフェンの絶縁体化への道筋を示したことで、デバイスなどの応用にも貢献すると期待できます。
グラフェンは、炭素原子が蜂の巣状につながった結晶構造をしています。その電子状態は質量ゼロの二次元ディラック電子[2]と同じ特殊な状態であることから、さまざまなユニークな性質を示すため、近年、注目を集めています。今回、国際共同研究グループは、スーパーコンピュータ「京」[3]を活用した「第一原理量子モンテカルロシミュレーション[4]」により、グラフェンを等方的に引っ張った場合にどのように電子状態が変化するかを解析しました。その結果、これまで予想されていた半金属[5]から反強磁性[6]モット絶縁体[7]へと変化するのではなく、半金属から「ケクレ型に歪んだ状態」へと変化することが分かりました。さらに、この状態は「トポロジカルに非自明な状態[8]」である可能性も示されました。
本研究は、米国の科学雑誌『Physical Review Letters』オンライン版(8月8日付け)に掲載されました。
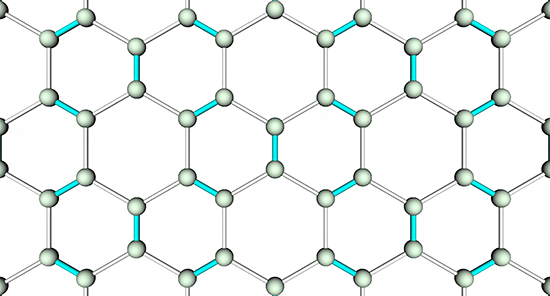
図 ケクレ型ダイマー状態の模式図(青で示した炭素原子間の距離が周期的に縮む)
※国際共同研究グループ
理化学研究所
計算科学研究センター 量子系物質科学研究チーム
客員主管研究員 サンドロ・ソレラ(Sandro Sorella)
(国際高等研究大学院大学(SISSA) 教授)
客員研究員 関 和弘(せき かずひろ)
(国際高等研究大学院大学(SISSA)、日本学術振興会海外特別研究員)
客員研究員 白川 知功(しらかわ とものり)
(国際高等研究大学院大学(SISSA)、Simons Foundation 研究員)
チームリーダー 柚木 清司(ゆのき せいじ)
(研究開拓本部 柚木計算物性物理研究室 主任研究員、創発物性科学研究センター 計算量子物性研究チーム チームリーダー)
創発物性科学研究センター 計算量子物性研究チーム
特別研究員 宮腰 祥平(みやこし しょうへい)
国際理論物理学センター(ICTP) Condensed Matter and Statistical Physics(イタリア)
博士研究員 オレッグ・ブロヴコ(Oleg O. Brovko)
国際高等研究大学院大学(SISSA) Condensed Matter Theory(イタリア)
教授 エリオ・トサッティー(ErioTosatti)
※研究支援
本研究は、HPCIシステム「京」一般課題「第一原理量子モンテカルロシミュレーションによるグラフェンおよびその派生物質の磁性と超伝導(課題番号:hp160126 課題代表者:柚木清司)」、「第一原理量子モンテカルロシミュレーションによるキャリア注入したグラフェンにおけるトポロジカル超伝導の探求(課題番号:hp170079 課題代表者:柚木清司)」、「第一原理量子モンテカルロシミュレーションによるグラフェンの圧力誘起半金属-絶縁体転移(課題番号:hp170308 課題代表者:柚木清司)」による支援を受けて行われました。
背景
鉛筆の芯などで馴染み深いグラファイト(黒鉛)は、炭素の二次元シートが積層した構造をしていますが、この二次元シートを1枚だけ取り出した炭素原子1個の厚みの物質を「グラフェン」と呼びます。グラフェンは、2004年にアンドレ・ガイム博士とコンスタンチン・ノボセロフ博士がグラファイトをセロハンテープで剥がすという実験で初めて作製されました。その功績により、両博士は2010年にノーベル物理学賞を受賞しています。
グラフェンは、正六角形の頂点に位置した炭素原子がつながることで蜂の巣状になった結晶構造をしており、その電子状態は質量ゼロの二次元ディラック電子と同じ特殊なものです。グラフェンは、この電子状態に起因するさまざまなユニークな性質を持つため、近年、注目を集めています。例えば、グラフェンで実現している質量ゼロのディラック電子(半金属状態)に、どのようにしたら有限の質量を持たせられる(絶縁体状態にする)かは、基礎物理の問題としてだけでなく、グラフェンを機能性材料として利用する応用でも重要な問題です。
この問題を解く方法の一つとして、最近実験で可能になったグラフェンを引っ張ることが挙げられます。グラフェンを等方的に引っ張ると炭素原子間の距離が大きくなるために、電子は炭素原子間を飛び移りにくくなり、相対的にそれぞれの炭素原子上での電子間クーロン相互作用(二つの電子が反発し合う力の作用)の影響が強くなります。すると、電子が各炭素原子上に局在するようになり、絶縁体化してモット絶縁体になります。局在化した電子のスピン[9]は、隣同士で逆向きになった方がエネルギー的に安定となるため、磁性(反強磁性)が出現します。これが従来予想されていたシナリオです(図1)。
実際に2016年、柚木チームリーダーらも、グラフェン上で働く電子間クーロン相互作用の効果を最も簡単な形で取り入れた格子模型(ハバード模型[10])に対するシミュレーションを行い、このシナリオを支持する結果を得ました注1)。しかし、格子模型により得られた絶縁体化のシナリオが、現実の引っ張られたグラフェンの絶縁体化のシナリオに当てはまるか否かの検証は、課題として残されました。その検証には、電子間クーロン相互作用の効果に加えて、格子模型を越えてグラフェンの結晶構造の歪みの可能性など、原子配置の自由度を直接的に扱う「第一原理シミュレーション」が必要でした。
注1)2016年3月19日プレスリリース「ディラック電子系に潜む普遍性を実証」
研究手法と成果
グラフェンを等方的に引っ張った場合、電子間クーロン相互作用の影響が電子の運動エネルギーよりも相対的に重要になると考えられます。国際共同研究グループはこの効果を精度良く取り扱うために、ソレラ客員主管研究員が中心となって開発している「第一原理量子モンテカルロ法」(図2)による大規模並列シミュレーション注2)をスーパーコンピュータ「京」を用いて行いました。
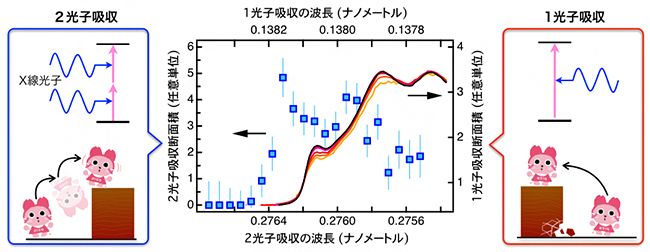
まず、実験で実現している張力一定の条件でのグラフェンの安定な原子構造と電子状態を決定するために、熱力学の状態量の一つであるエンタルピー[11]を計算しました(図3)。その結果、従来予想されていた反強磁性絶縁体状態は安定にならず、代わりに、隣り合う炭素原子が互いに対(ダイマー)を作って規則正しく並んだ「ケクレ型ダイマー状態」が安定になることが分かりました。対になった炭素原子間の距離は周期的に縮むため、歪んだ構造となります。この状態は磁性を示さず、グラフェンをさらに引っ張っても反強磁性絶縁体状態になることなく壊れてしまいました(図4)。
ところで、ケクレ型ダイマー状態にある炭素原子6個が作る六角形に注目すると、これは、量子力学を化学に応用した先駆者であるライナス・ポーリング博士が提唱したベンゼン分子で見られる共鳴原子価結合(RVB)状態[12]と似ています。ベンゼン分子の電子状態を量子力学に従って正しく記述するためには、電子間クーロン相互作用が考慮されない一つのスレーター行列式[13]では不十分で、多数のスレーター行列式が必要なことが知られています。つまり、RVB状態を記述するためには多体効果[14]が本質的に重要です。
今回の結果は、まさにこのRVB状態と電子間クーロン相互作用とを取り込める理論計算によって可能になりました。実際に、第一原理計算[4]の枠組みでも、電子状態をRVB状態ではなく、一つのスレーター行列式で表す計算では、ケクレ型ダイマー状態は安定ではありませんでした。これは、第一原理量子モンテカルロシミュレーションで発見したケクレ型ダイマー状態が、炭素原子の結晶構造の歪みによって誘発されたのではなく、電子状態が電子間クーロン相互作用によりRVB的な状態になったことで引き起こされたことを示しています。
さらに、このケクレ型ダイマー状態は、先行研究注3,4)でも提案されていたタイプの「対称性に保護されたトポロジカル相[15](トポロジカルに非自明な状態相)」に属する可能性も示しました。トポロジカルに非自明であるためには、この場合、結晶の対称性(カイラル対称性[16]と鏡映対称性)が本質的で、例えば、その対称性を破らないようにグラフェンを切った場合、その切断面にゼロエネルギー状態が現れるという特徴を持っています(図5)。
注2) 開発されているソフトフェアは「TurboRVB」と呼ばれる。
注3) T. Kariyado and X. Hu, “Topological States Characterized by Mirror Winding Numbers in Graphene with Bond Modulation”, Scientific Reports 7, 16515 (2017);
注4) F. Liu, M. Yamamoto, and K. Wakabayashi, “Topological Edge States of Honeycomb Lattices with Zero Berry Curvature”, Journal of the Physical Society of Japan 86, 123707 (2017).
今後の期待
グラフェンは、基礎物理だけでなく応用面でも大きく注目されています。今回のシミュレーションの結果は、グラフェンの新たな可能性を予言するものであり、今後の実験的な検証が待たれます。ケクレ型ダイマー状態は非磁性絶縁体ですが、この状態に動き回れるキャリア(電子あるいは正孔)を注入した場合にどのような状態が現れるかは、さらに興味深い問題です。固体物理学研究者が長年待ち望んでいたRVB超伝導[17]が現れるかもしれません。
また、本研究では、「京」を活用した第一原理量子モンテカルロシミュレーションが威力を発揮しました。この手法は、電子間クーロン相互作用が強い物質群に対するシミュレーションで特に力を発揮するため、さらにユニークな電子状態の発見が期待できます。
原論文情報
- S. Sorella, K. Seki, O. O. Brovko, T. Shirakawa, S. Miyakoshi, S. Yunoki, E. Tosatti, “Correlation-Driven Dimerization and Topological Gap Opening in Isotropically Strained Graphene”, Physical Review Letters, 10.1103/PhysRevLett.121.066402
発表者
理化学研究所
計算科学研究センター 量子系物質科学研究チーム
客員主管研究員 サンドロ・ソレラ(Sandro Sorella)
(国際高等研究大学院大学(SISSA) 教授)
客員研究員 関 和弘(せき かずひろ)
(国際高等研究大学院大学(SISSA) 日本学術振興会海外特別研究員)
客員研究員 白川 知功(しらかわ とものり)
(国際高等研究大学院大学(SISSA) Simons Foundation研究員)
チームリーダー 柚木 清司(ゆのき せいじ)
(研究開拓本部柚木計算物性物理研究室 主任研究員、創発物性科学研究センター 計算量子物性研究チーム チームリーダー)
創発物性科学研究センター 計算量子物性研究チーム
特別研究員 宮腰 祥平(みやこし しょうへい)
報道担当
理化学研究所 広報室 報道担当
補足説明
-
- グラフェン
- 炭素原子が2次元上に並んだシート状物質。各炭素原子は、sp2結合により正六角形がつながった蜂の巣状の格子を組む。
-
- ディラック電子
- 量子力学に相対論的効果を取り込んだ運動方程式に従う電子。
-
- スーパーコンピュータ「京」
- 文部科学省が推進する「革新的ハイパフォーマンス・コンピューティング・インフラ(HPCI)の構築」プログラムの中核システムとして、理研と富士通が共同で開発を行い、2012年9月に共用を開始した計算速度10ペタフロップス級のスーパーコンピュータ。スーパーコンピュータの性能ランキング(TOP500)で2011年に世界1位を獲得した。
-
- 第一原理量子モンテカルロシミュレーション、第一原理計算
- 固体の運動方程式(シュレーディンガー方程式)は、原子の種類と位置を与えれば書き下せる。この運動方程式を量子力学の法則に従って直接解く計算を、第一原理計算と呼ぶ。その第一原理計算の中で、電子間クーロン相互作用の効果をより精密に扱うために考案された量子モンテカルロ法を利用した方法を、第一原理量子モンテカルロシミュレーションと呼ぶ。
-
- 半金属
- 本来はバンド理論による電子状態の分類の一つで、価電子帯と伝導帯にギャップが開いていて一見半導体のように見えるが、フェルミ準位がこの二つのバンドを小さくまたいでいるものを半金属と呼ぶ。グラフェンの場合、価電子帯と伝導帯はフェルミ準位上の点で重なっているので、上記の意味とは異なるが、この「点で重なっている」という、通常の金属とは違う特殊な状況を表す意味で「半金属」という呼称が定着してしまった。
-
- 反強磁性
- 電子のスピンが全て同じ向きにそろっている場合を強磁性、隣り合うスピンがそれぞれ反対方向を向いて整列し、全体として磁気モーメントを持たない場合を反強磁性という。
-
- モット絶縁体
- 電子間クーロン相互作用(二つの電子が互いに反発し合う斥力)が大きいために電子が動けなくなって全体として絶縁化を起こす絶縁体。
-
- トポロジカルに非自明な状態
- 波動関数によって定義される、あるトポロジカル不変量によって通常の状態と区別できる状態。
-
- スピン
- 電子は原子核の周りを回転運動していると共に、自転していると考えられている。この自転に対応する物理量をスピンと呼ぶ。右回転と左回転の自転に対応してスピンは、「上向き」と「下向き」の二つがある。
-
- ハバード模型
- 第一原理計算に使う運動方程式の中で、原子の最外殻付近の電子軌道のみを取り出し、その中で電子が隣り合う原子間を飛び回ることで得られる運動エネルギーと、同一原子上に二つの電子が同時に来た場合に働く電子間クーロン相互作用のみを考慮した模型。
-
- エンタルピー
- 熱力学の法則では、絶対零度では、体積V(本研究の2次元系の場合は面積(S))を決めたときにエネルギーEを最小化する状態が実現する。これに対し、圧力P(2次元系の場合は張力(σ))を与えたときに実現する状態は、エンタルピーH=E+PV(2次元系の場合はH=E-σS)を最小化するものとなる。実験で「引っ張る」とは、張力を制御することなので、系の安定性はエンタルピーで評価される。なお、今回の計算は絶対零度で行っている。
-
- 共鳴原子価結合(RVB)状態
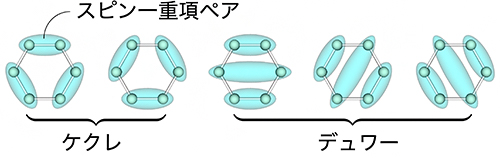
- 格子を考え、その格子上のどの格子点にも一つの電子がある状況を考える。その中で、ある格子点の電子は別のある格子点の電子と必ずスピン一重項(量子力学的なスピンの逆向き状態)のペアを組ませることにすると、ペアで格子が埋め尽くされ、“ペアの配置”が一つ決まる。考えうるペアの配置は無数にあるが、RVB状態とはこの無数のペアの配置の「重ね合わせ状態」として考案された状態。多体効果によって顕在化する状態の一つと考えられ、ベンゼン分子のRVB状態がよく知られている。ベンゼン分子では、ケクレ型とデュワー型のペアの配置がある。RVBは resonating valence bondの略。
-
- スレーター行列式
- 多電子状態をパウリ排他律に従って記述するときに用いる行列式。一つのスレーター行列式による多電子状態の記述では、電子間クーロン相互作用は全く考慮されない。
-
- 多体効果
- 電子間クーロン相互作用の影響が大きくなってくると、ある電子は別の電子に影響を与え、その別の電子はまた別の電子に影響を与えていくため、全ての電子がお互いに影響を及ぼし合う状況になる。このような一つの電子のみを考えただけでは説明できないような性質を生み出す効果を多体効果と呼ぶ。多体効果が顕著な多電子状態の記述には、一つのスレーター行列式では不十分で多数のスレーター行列式が必要である。
-
- 対称性に保護されたトポロジカル相
- ある対称性がある場合にのみ、トポロジカルに自明な状態と区別できるトポロジカルに非自明な状態相を「対称性に保護されたトポロジカル相(symmetry protected topological phase、SPTと略される)」と呼ぶ。トポロジカルに自明な相と非自明な相の状態は断熱変化(徐々に変化させること)でつなげることができないが、SPTの場合は、保護する対称性を破ると状態を断熱変化によってつなげることができるため、区別できなくなる。
-
- カイラル対称性
- 一般にはディラック方程式のカイラル変換に対する対称性を表す。グラフェンの場合には、結晶構造を構成する最小ユニット内にある二つの炭素原子の入れ替えに対する対称性。
-
- RVB超伝導
- RVB型絶縁体にキャリアをドープすることで出現すると理論的に提案された超伝導状態。
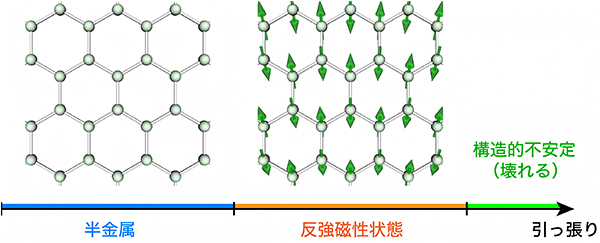
図1 グラフェンを等方的に引っ張った場合の予想されていた従来の相図(模式図)
ある大きさの引っ張り力を境に電子が各炭素原子上に局在し、電子のスピン(緑の矢印)が隣同士で逆向きに整列する反強磁性状態が実現すると考えられていた。
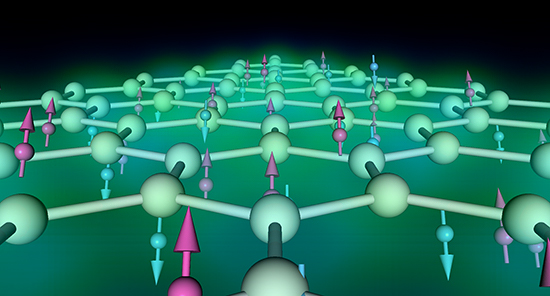
図2 第一原理量子モンテカルロシミュレーションの概念図
量子力学的な多電子状態は、「波動関数」(図では霧のように表現)と呼ばれる全ての電子(図中の矢印付きの球)の位置(電子配置)の関数で記述される。第一原理量子モンテカルロシミュレーションでは、この波動関数が決める電子の密度(電子雲)に従って電子配置のサンプルを発生させ、サンプルから見積もられるエネルギーが低くなるように波動関数と原子構造を最適化していく。
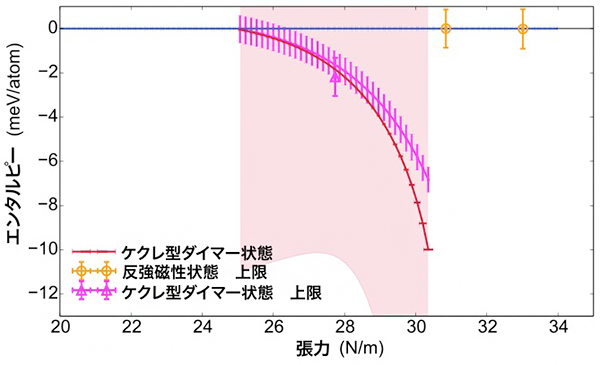
図3 グラフェンの半金属状態を基準としたエンタルピーと張力の関係
与えられた張力に対して、エンタルピーが低い状態が安定となる。“上限”とあるのは、各状態のエンタルピーの上限を与える計算結果で、エンタルピーそのものの計算と比べて安定性を過小評価するが統計誤差が少ない。この図は、張力が約25N/mから約30N/mのときケクレ型ダイマー状態が安定となることを示している。
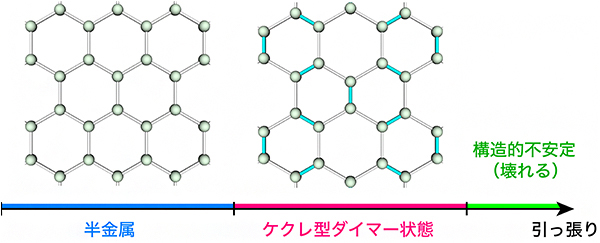
図4 グラフェンを引っ張った場合の本研究により得られた相図(模式図)
従来予想されていた反強磁性状態ではなく、隣り合う炭素原子が互いに対になって規則正しく並んだ「ケクレ型ダイマー状態」が出現した。この状態では、白で示した炭素原子間の距離に比べて、青で示した炭素原子間の距離が周期的に縮むため、歪んだ構造となる。
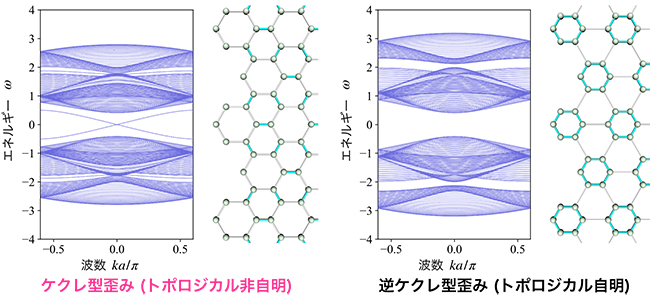
図5 トポロジカルに非自明な状態を切断したときに切断面に出現するゼロエネルギー状態
左図のように、ケクレ型歪みを持つグラフェンを切断した場合、表面にゼロエネルギー状態が生じる。右図のように、トポロジカルに自明となる逆ケクレ型歪みを持つグラフェンを切断した場合、表面にゼロエネルギー状態は生じない。このとき、どちらの切断も対称性(カイラル対称性と鏡映対称性)を壊さない。