パルス光照射による「ηペアリング状態」の実現を予言
2019-02-23 理化学研究所
理化学研究所(理研)開拓研究本部柚木計算物性物理研究室の金子竜也基礎科学特別研究員、柚木清司主任研究員、計算科学研究センター量子系物質科学研究チームの白川知功客員研究員、サンドロ・ソレラ客員研究員の研究チームは、モット絶縁体[1]にパルス光を照射することにより、「ηペアリング状態[2]」と呼ばれる珍しい超伝導[3](ηペアリング超伝導)が生じ得ることを、スーパーコンピュータ「京」[4]などによる計算機シミュレーションをもとにして理論的に予言しました。
本研究成果は、非平衡状態[5]のダイナミクスで現れる光誘起現象[6]の新たな側面を明らかにしたのみでなく、現在さまざまな場面で利用されている超伝導の応用の可能性をさらに広げるものとして期待できます。
ηペアリング状態は、30年前に純粋な数学的議論により提案されました。しかし、この状態は励起状態であり、しかも励起状態は数多く存在するため、実験的に実現することが難しく、これまでは数学の世界で現れる“虚像”と考えられてきました。
今回、研究チームは、モット絶縁体にパルス光を照射した場合の非平衡ダイナミクスを理論的に解析しました。その結果、光励起された状態でηペアリング状態が誘起されていることを明らかにしました。また、その背景に対称性に基づく美しい数理構造があることも指摘しました。
本研究は、米国の科学雑誌『Physical Review Letters』の掲載に先立ち、オンライン版(2月22日付け:日本時間2月23日)に掲載されます。

図 モット絶縁体に光(黄)を照射することで誘起される「ηペア」(緑の電子対)のイメージ
※研究支援
本研究は、日本学術振興会(JSPS)科学研究費補助金若手研究「励起子絶縁体の光誘起ダイナミクスに関する理論的研究(研究代表者:金子竜也)」、同基盤研究B「対称性が自発的に破れた二次元反強磁性体のマグノン励起とスピノン励起の数値解析(研究代表者:柚木清司)」、同基盤研究C「時間発展行列積状態を基にしたスピン流の微視模型解析(研究代表者:白川知功)」などの支援を受けて行われました。
背景
「超伝導」は電気抵抗がゼロになる現象で、現在では、リニアモーターカーや核磁気共鳴画像(MRI)装置[7]など私たちの身の回りのさまざまな場面で既に応用されています。
超伝導現象は、通常、金属を極低温まで冷やすことで現れますが、これを引き起こすメカニズムは、大きく分けて二つ知られています。電子が結晶格子の振動と相互作用することで引き起こされる従来型超伝導と、電子間のクーロン相互作用で引き起こされる非従来型超伝導です。前者には、ニオブ-チタンやニオブスズ、ニホウ化マグネシウムなどの化合物が、後者には、ヘリウム3(3He)や銅酸化物高温超伝導体などが知られています。
一方、近年、物質にパルス光を照射することにより、物理量が時間に依存して変化する「非平衡状態」で生じる現象の研究が盛んに行われています。その一つとして、電気が流れない絶縁体、特に、電子間クーロン相互作用により絶縁体化した「モット絶縁体」にパルス光を照射し、非平衡状態でモット絶縁体を金属、さらには超伝導にしようとする試みもなされています。
このような光誘起された状態の研究は、非平衡状態のダイナミクスの基礎学理としても非常に重要です。ただし、この光誘起状態は、そのほとんどが、圧力やキャリア濃度などが異なる「平衡状態[5]」で実現している状態を、別の状況下で光照射によって誘発させたもので、光照射によってできた全く新しい状態というよりは、ある状況下において実現していた状態を、別の状況下で光照射によって誘発させたものと考えられています。
研究手法と成果
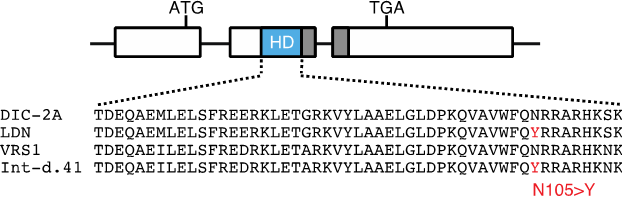
研究チームは、ハバード模型[8]で実現しているモット絶縁体に、パルス光を照射した場合に起こる非平衡ダイナミクスを、スーパーコンピュータ「京」などによる計算機シミュレーションをもとにして理論的に解析しました。その結果、光励起した状態が、同じ格子サイトで電子対を形成した超伝導相関を非常に強く示すことを発見しました(図1a)。しかも、超伝導相関の符号をよく調べると、図1bのように正負に振動していることが分かりました。これは、まさに「ηペアリング状態」と呼ばれる超伝導(ηペアリング超伝導)に特有な振る舞いです。
ηペアリング状態は、スピン[9]の向きが異なる二つの電子が同じ格子サイトで対(電子対)を形成し、その位相が隣り合うサイト同士で180度異なるという珍しい電子対(ηペア[2])が多数集まってできた状態です。この状態は、数理物理学者の楊振寧が約30年前に、ハバード模型の厳密な固有状態であることを示しました。しかし、ηペアリング状態は励起状態であり、しかも励起状態は数多く存在するため、実験的に実現することが難しく、一部の数理物理学者を除いて、現在まであまり注目を集めていませんでした。本研究結果により、この珍しい電子状態が、パルス光照射という比較的簡単な実験で実現できることを理論的に予言したことになります。
さらに、研究チームは、ハバード模型の隠れた対称性とそれに基づく数理構造を用いた解析から、パルス光を照射することで、ηペアを一つずつ選択的に生成できることを突き止めました(図2)。つまり、パルス光照射により多くのηペアが生成された結果、ηペアリング状態が光誘起されるというシナリオです。
今後の期待
本研究では、モット絶縁体にパルス光を照射することにより、選択的にηペアリング状態を誘起できることを、計算機シミュレーションをもとにして理論的に予言しました。ηペアリング超伝導を、今後パルス光照射実験で観測できれば画期的なマイルストーンとなります。ηペアリング超伝導は、発現メカニズムが従来の超伝導とは異なり、この点でもηペアリング超伝導の実験的観測は重要です。
現在、超伝導は、私たちに近いさまざまな場面への応用化が進んでいます。パルス光で誘起できるηペアリング超伝導は、超伝導の応用の可能性をさらに広げるものとして期待できます。
原論文情報
T. Kaneko, T. Shirakawa, S. Sandro, and S. Yunoki, “Photoinduced η-pairing in the Hubbard Model”, Physical Review Letters
発表者
理化学研究所
主任研究員研究室 柚木計算物性物理研究室
基礎科学特別研究員 金子 竜也(かねこ たつや)
主任研究員 柚木 清司(ゆのき せいじ)
(創発物性科学研究センター 計算量子物性研究チーム チームリーダー、 計算科学研究センター 量子系物質科学研究チーム チームリーダー)
計算科学研究センター 量子系物質科学研究チーム
客員研究員 白川 知功(しらかわ とものり)
(国際高等研究大学院大学(SISSA) Simons Foundation研究員)
客員主管研究員 サンドロ・ソレラ(Sandro Sorella)
(国際高等研究大学院大学(SISSA) 教授)
報道担当
理化学研究所 広報室 報道担当
補足説明
-
- モット絶縁体
- 電子密度が1原子あたり奇数個の場合に、電子間クーロン斥力がないあるいは弱いと金属であるが、電子間クーロン斥力が大きいために電子が動けなくなって絶縁化を起こした絶縁体。
-
- ηペアリング状態、ηペア
- ηペアは、互いに反対向きのスピン[9]を持つ二つの電子が同じサイト上でペアを組み、その電子対の波動関数の位相が隣り合うサイトごとに180°変調したパターンを示す特殊な電子対のことである。ηペアリング状態は、多数のηペアで構成された電子全体の状態。超伝導状態の指標となる非対角長距離秩序を有し、かつハバード模型[8]の厳密な固有励起状態となっている。
-
- 超伝導
- 金属を十分に低温にすることで電気抵抗が急激にゼロになる現象。ニつの電子が対を形成して引き起こす現象である。
-
- スーパーコンピュータ「京」
- 文部科学省が推進する「革新的ハイパフォーマンス・コンピューティング・インフラ(HPCI)の構築」プログラムの中核システムとして、理研と富士通が共同で開発を行い、2012年9月に共用を開始した計算速度10ペタFLOPS級のスーパーコンピュータ。スーパーコンピュータの性能ランキング(TOP500)で2011年に世界1位を獲得した。
-
- 平衡状態、非平衡状態
- 時間の変化に対して巨視的な物理量が変わらない状態が平衡状態。外場などによって平衡状態が崩れ、物理量が時間に依存して変化する状態を非平衡状態と呼ぶ。
-
- 光誘起状態
- パルス光などの照射によって生じる非平衡過程を経て誘起される状態。
-
- 核磁気共鳴画像(MRI)装置
- 磁力中における水素原子の核スピンの共鳴現象により、人体などの断面撮像を行う装置。脳や血管などの画像診断に広く使われ、磁力を高くすることにより、より高分解能の診断が可能となる。MRIはMagnetic Resonance Imagingの略。
-
- ハバード模型
- 隣り合う原子間を電子が飛び移ることで得られる運動エネルギーと、同一格子サイト上に二つの電子が同時に来た場合に働く電子間クーロン相互作用からなる模型。モット絶縁体を記述する最も基礎的な模型である。
-
- スピン
- 電子が右回りまたは左回りに自転する回転の内部自由度のこと。この回転の向きに応じて上向きまたは下向きの矢印で表される。
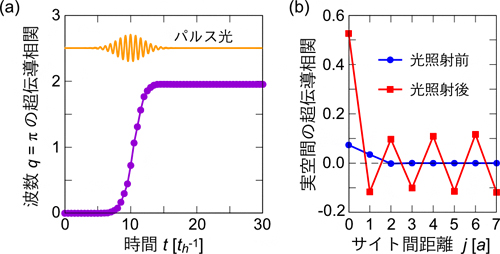
図1 理論計算によって得られたパルス光照射によるハバード模型の超伝導相関関数
(a) パルス光照射により、波数q=π(位相180°)における超伝導相関関数が上昇している。
(b) 光照射前(モット絶縁体状態)と光照射後(光誘起状態)の実空間における超伝導相関関数の比較。光照射後の相関関数はサイトごとに正負に振動しており、「ηペアリング状態」に特有な振る舞いを示している。サイト間(距離:a)の遷移積分thの逆数を時間の単位にしている。ここでは、二つの電子が同じ格子サイトで電子対を形成した場合の超伝導相関を計算している。
図2 ハバード模型の固有状態分布とηペアリング状態間に対する選択則の模式図
(a) 少数格子サイトで計算したハバード模型の全固有状態。横軸が各固有状態のエネルギーで、縦軸が超伝導相関関数を示している。ハバード模型が持つ対称性に基づき、相関関数の値が「ηペア」の数に応じて綺麗に離散化している。ここでは、サイト間遷移積分thをエネルギーの単位にしている。各点の色は光誘起状態における各固有状態の重みを示しており、ηペアを有限に持つ固有状態が重みを持っていることが分かる。これが光照射による超伝導相関上昇の本質的な原因である。
(b) パルス光の周波数をハバード模型の斥力相互作用U程度に調整すると、矢印で示したような状態への遷移だけが許され、図のような「ηペアリング」状態間の選択則が成立する。これは、(a)の固有状態の重み分布と定性的に一致している。