2023-01-24 東京大学
発表者
今泉 允聡（東京大学 大学院総合文化研究科 広域科学専攻 准教授）
Johannes Schmidt-Hieber（University of Twente, Professor）
発表のポイント
- 深層学習が過学習を起こさない原理を、ニューラルネットワークがエネルギー曲面上で滞留する数学的理論を開発して説明した。
- 深層学習が大自由度にも関わらず過学習しない原理は長年の未解明点であり、これを説明する理論を開発した。
- 深層学習を効率的に制御するための理論の発展や、アルゴリズム開発・ネットワーク設計などへの工学的応用が期待される。
発表概要
東京大学大学院総合文化研究科の今泉允聡准教授、University of TwenteのJohannes Schmidt-Hieber教授による研究チームは、ニューラルネットワーク（注1）がエネルギー曲面上（注2）で”滞留”という現象を起こすことを数学的に記述し、深層学習が過学習（注3）を起こさない原理を説明する新理論を開発しました。深層学習が大量のパラメータを持ちながらも過学習をしない理由は、近年多くの仮説が提起されつつも未だに十分には明らかにされていません。今回の成果は、滞留の概念を用いてアルゴリズムの確率的挙動を記述することで、深層学習が汎用的な知識を獲得する現象への新しい理論的基礎づけを与えました。今後は、より具体的な深層学習の理論の発展や、深層学習の高速化につながるアルゴリズムの開発などにつながることが期待されます。
本研究成果は、2023年1月20日（米国東部時間）に米国科学誌「IEEE Transactions on Information Theory」のオンライン版に掲載されました。
発表内容
＜研究の背景・先行研究における問題点＞
深層学習は非常に高い性能を発揮するデータ解析技術で、現代の人工知能の中核技術のひとつです。しかしその実用性の高さに比して、なぜ高い性能が出るのかという仕組みは未だ明らかになっておらず、今後の技術発展や安全な実用のために理論的な説明が求められています。特に重要度の高い未解決問題として、ニューラルネットワークの過学習の問題があります。深層学習で用いられるニューラルネットワークは、大量のパラメータを持つためその自由度が大変高いですが、訓練データに対して過剰に適合する”過学習”という現象が起こらないということが実験的に観察されています。これは大量のパラメータが過学習により精度を下げるという従来の理論と大きく矛盾しており、この問題を解消する理論が必要とされています。有力な仮説として、学習アルゴリズムの挙動が自由度を下げるという暗黙的正則化仮説が提唱されていますが、その具体的な形は未だに定説がありません。
＜研究内容＞
東京大学大学院総合文化研究科の今泉允聡准教授、University of TwenteのJohannes Schmidt-Hieber教授による研究チームは、ニューラルネットワークがエネルギー曲面上で”滞留”という現象を起こすことを数学的に記述し、これが暗黙的な正則化となって深層学習が過学習を起こさないとする新理論を開発しました。ニューラルネットワークが学習を行う際には、確率的なアルゴリズムに基づいてエネルギー曲面上を遷移し、最適なパラメータを探索します。今回開発された理論では、このエネルギー曲面にある極小値の近傍が特定の構造を持つ際に、ニューラルネットワークがこの近傍に高確率で滞留し、これが暗黙的な正則化となって深層学習の過学習が起こらなくなることを証明しました（図1、2）。これまでの学説で、暗黙的正則化の具体的内容は数多く提案されてきましたが、有力な仮説に実験的な反例が出されるなど、有効な形は未だ定まっていませんでした。本研究によって、数学的に有効な形で暗黙的正則化の具体的な形が提唱されました。
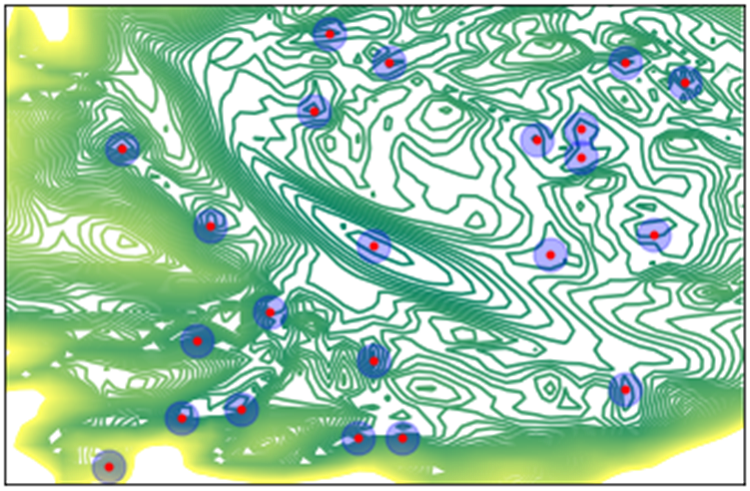
図1．ニューラルネットワークのエネルギー曲面を次元圧縮したものの可視化（等高線）。極小値（赤い丸）とその近傍（青い丸）が滞留を起こしうる領域を表す。
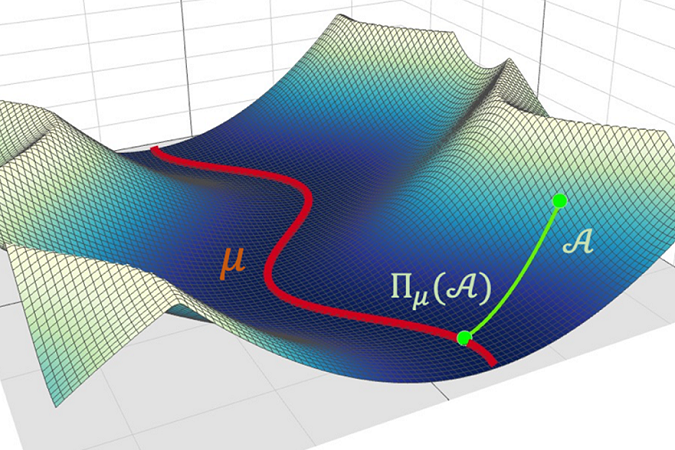
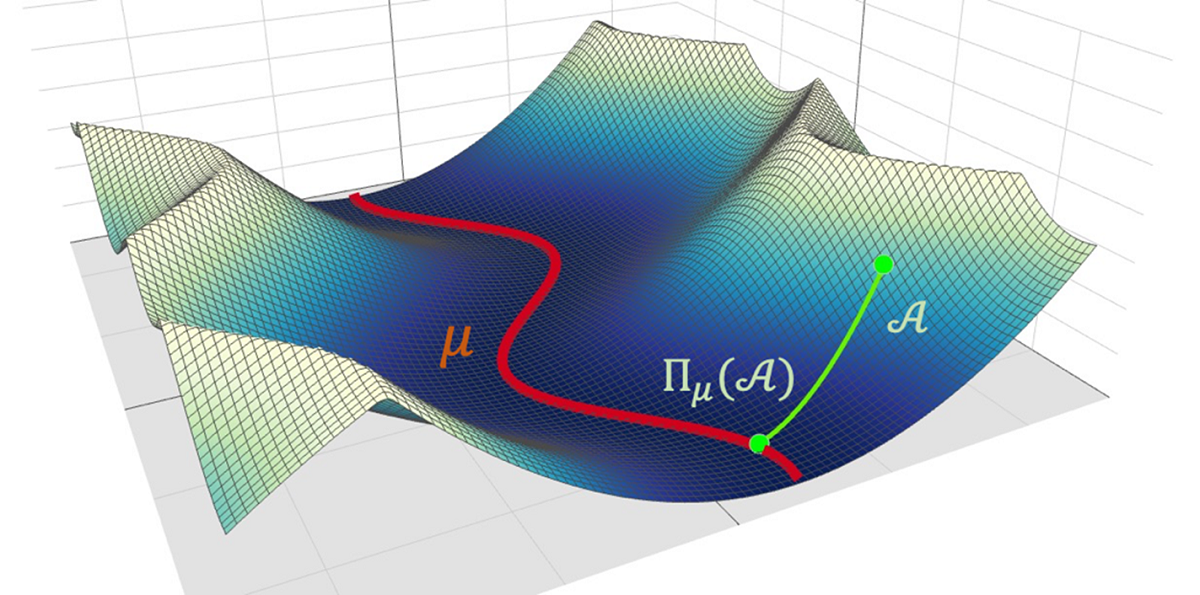図2．エネルギー曲面中の極小値とその近傍のイメージ図。エネルギー曲面中の極小値の近傍で局面が理想的な形状を持つ場合、その極小値は滞留を引き起こしうる。
＜社会的意義・今後の予定＞
深層学習は高い性能を発揮できるデータ解析手法ですが、その原理は未だ不明な点が多く、また計算コストの大きさや解釈性の低さといった実用上の問題点が多く残っています。本研究の成果は、深層学習の原理を解明するといった理論の試みに貢献し、人工知能のための新しい数学の構築につながるといった学術的な発展に加えて、ニューラルネットワーク設計や学習を効率化するアルゴリズムなどの工学的応用につながると考えられます。
本研究は、JSPS科研費「深層学習の原理究明に向けた関数推定理論の開発（課題番号：JP18K18114）」、JSTさきがけ「深層学習の高速化にむけた適応ネットワークの数学的発見と学習法開発（課題番号：JPMJPR1852）」の支援により実施されました。
論文情報
雑誌：「IEEE Transactions on Information Theory」（オンライン版：2023年1月20日掲載）
論文タイトル：On Generalization Bounds for Deep Networks based on Loss Surface Implicit Regularization
著者：Masaaki Imaizumi*, Johannes Schmidt-Hieber
DOI番号：10.1109/TIT.2022.3215088
用語説明
（注1）ニューラルネットワーク：
深層学習で用いられる数理的なモデル（模型）。多くのパラメータを持ち、これらを更新することで訓練データの情報やその内部構造を学習する。
（注2）エネルギー曲面：
ニューラルネットワークと訓練データの乖離度（損失）で描かれる関数の表面。深層学習のエネルギー曲面は非常に複雑な構造を持つことが知られている。
（注3）過学習：
ニューラルネットワークなどのモデルが訓練データに過剰に適合し、新しいデータの元での予測などに失敗する現象。パラメータの数が非常に大きいモデルは過学習が起こりやすいと考えられていたが、実際のニューラルネットワークはそのケースに当てはまらない。
