2022-05-03 アルゴンヌ国立研究所(ANL)
米国エネルギー省(DOE)のアルゴンヌ国立研究所の科学者たちは、さらに別の用途で強化学習アルゴリズムを開発しました。それは、原子や分子のスケールで材料の特性をモデル化するためのもので、材料の発見を大幅にスピードアップさせるはずです。
<関連情報>
- https://www.anl.gov/article/machine-learning-program-for-games-inspires-development-of-groundbreaking-scientific-tool
- https://www.nature.com/articles/s41467-021-27849-6
高次元ポテンシャルエネルギーモデル開発のための連続作用空間における学習 Learning in continuous action space for developing high dimensional potential energy models
Sukriti Manna,Troy D. Loeffler,Rohit Batra,Suvo Banik,Henry Chan,Bilvin Varughese,Kiran Sasikumar,Michael Sternberg,Tom Peterka,Mathew J. Cherukara,Stephen K. Gray,Bobby G. Sumpter & Subramanian K. R. S. Sankaranarayanan
Nature Communications Published: 18 January 2022
DOI:https://doi.org/10.1038/s41467-021-27849-6
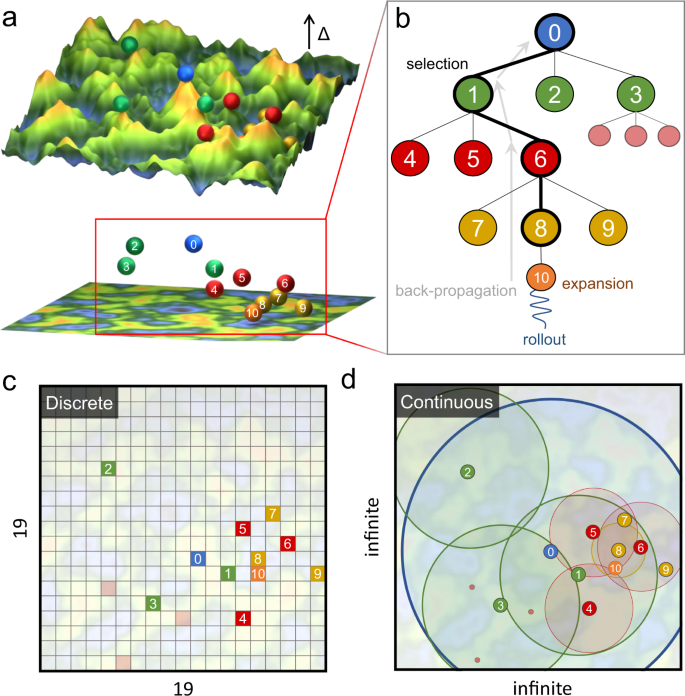
Abstract
Reinforcement learning (RL) approaches that combine a tree search with deep learning have found remarkable success in searching exorbitantly large, albeit discrete action spaces, as in chess, Shogi and Go. Many real-world materials discovery and design applications, however, involve multi-dimensional search problems and learning domains that have continuous action spaces. Exploring high-dimensional potential energy models of materials is an example. Traditionally, these searches are time consuming (often several years for a single bulk system) and driven by human intuition and/or expertise and more recently by global/local optimization searches that have issues with convergence and/or do not scale well with the search dimensionality. Here, in a departure from discrete action and other gradient-based approaches, we introduce a RL strategy based on decision trees that incorporates modified rewards for improved exploration, efficient sampling during playouts and a “window scaling scheme” for enhanced exploitation, to enable efficient and scalable search for continuous action space problems. Using high-dimensional artificial landscapes and control RL problems, we successfully benchmark our approach against popular global optimization schemes and state of the art policy gradient methods, respectively. We demonstrate its efficacy to parameterize potential models (physics based and high-dimensional neural networks) for 54 different elemental systems across the periodic table as well as alloys. We analyze error trends across different elements in the latent space and trace their origin to elemental structural diversity and the smoothness of the element energy surface. Broadly, our RL strategy will be applicable to many other physical science problems involving search over continuous action spaces.



