2022-01-14 理化学研究所,東京大学大学院理学系研究科,東邦大学
理化学研究所(理研)開拓研究本部加藤分子物性研究室の藤山茂樹専任研究員(研究当時、現岩崎中間子科学研究室専任研究員)、加藤礼三主任研究員(現理研研究政策審議役)、東京大学大学院理学系研究科の前橋英明特任研究員、東邦大学理学部の田嶋尚也教授らの共同研究グループは、「ディラック電子系[1]」と呼ばれる物質の磁化率[2]と電気伝導度の間のスケーリング則[3](比例関係)を発見し、この電磁応答の統一が特殊相対性理論[4]における「時間と空間の対称性[5]」に対応していることを見いだしました。
本研究成果は、グラフェン[6]やトポロジカル絶縁体[7]など、次世代デバイスの候補材料における電磁応答の理解の基盤になると期待できます。
今回、共同研究グループは、分子性固体「α-(BETS)2I3[8]」が小さなエネルギーギャップ(電子状態が存在しないエネルギー範囲)を持つ二次元ディラック電子系物質であることを実験とバンド計算[9]から同定し、磁化率と電気伝導度を測定しました。二次元伝導面に垂直な方向にだけ生じる大きな軌道反磁性[10]磁化率を観測し、量子化された電気伝導度とのスケーリング則を導きました。この磁性と電気伝導の強い関係は、ゼロギャップディラック電子の分散[9]関係と光の分散[11]関係が同等であることに由来し、特殊相対性理論が導く時間と空間の対称性に対応していると考えられます。
本研究は、科学雑誌『Physical Review Letters』(1月14日号)の掲載に先立ち、オンライン版(1月12日付)に掲載されました。
背景
固体物質の機能は、内部の電子の電場や磁場に対する応答(電磁応答)によって表すことができ、現在も新たな機能を持つ物質の開発が活発に行われています。電磁応答の基礎は、電子分散(バンド構造[9])により与えられることから、特異な電子分散関係を持つ固体物質は未知の電磁応答を示す可能性が高くなります。
この特異な電子分散の例として「ディラック型電子分散」があります。電子分散がフェルミ準位[12]近傍でX字状に交差するもので、この分散を持つ物質はエネルギーギャップ(電子状態が存在しないエネルギー範囲)がゼロであり、「ゼロギャップディラック電子系」と呼ばれています(図1A)。近年注目されているグラフェンやトポロジカル絶縁体の表面状態もゼロギャップディラック電子系です。これらの物質に関して、電気伝導など電子輸送の研究が盛んに行われていますが、1mg以上の単結晶試料を必要とする磁化率の絶対値測定は難しく、これまであまり例がありませんでした。
ディラック電子系の電磁応答は、相対論的量子力学であるディラック方程式[13]で記述できます。特殊相対性理論の重要な結論は「時間と空間の統一(時間と空間の対称性)」で、光円錐[11]として示され(図1B)、これに対応するものは、電場応答と磁場応答の対称性として理論的に表現できます。しかし、固体中電子は光よりはるかに遅い速度で運動するため、相対論効果[5]である電磁応答の対称性は失われ、電気的性質と磁気的性質を統一的に扱うことはできない、とこれまで考えられてきました。
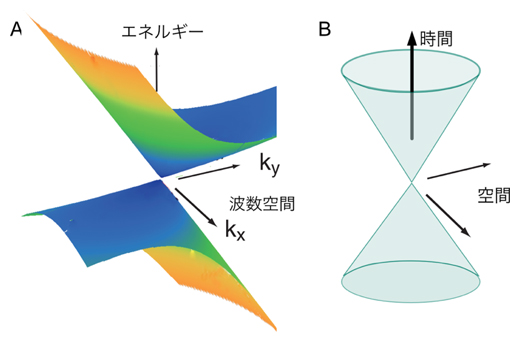
図1 ゼロギャップディラック型電子分散と時間と空間の対称性を示す光円錐
A:ゼロギャップディラック型電子分散の模式図。kx、kyは波数ベクトルを示す。電子分散がフェルミ準位近傍でX字状に交差している。
B:特殊相対性理論における時間と空間の対称性を示す光円錐。光はどの方向に対しても同じ光速度で進行するため円錐を形作る。光円錐とゼロギャップディラック電子系の電子分散とは、時間をエネルギーに、空間を波数空間に、1対1に対応づけることで等価性を示すことができる。
研究手法と成果
共同研究グループは、二次元層状構造をとる分子性固体「α-(BETS)2I3」の純良単結晶を合成し、電気伝導度、磁化率、13C核磁気共鳴(NMR)法[14]などの測定を行いました(図2)。また、X線結晶構造解析[15]のデータを用いたバンド計算、および実験データ全てを包括する理論の構築を目指しました。
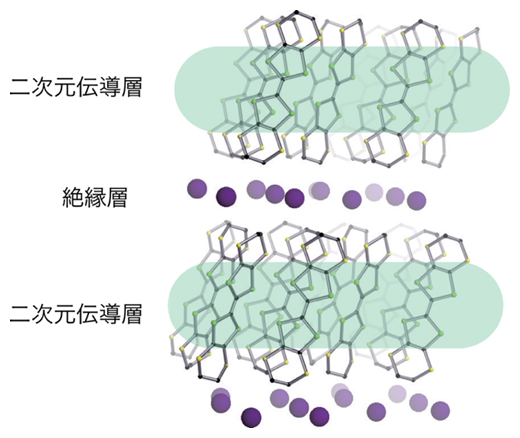
図2 分子性固体α-(BETS)2I3の結晶構造
今回合成した分子性固体α-(BETS)2I3の結晶構造。BETS分子が二次元伝導層を形成する。絶縁層にある紫丸が三ヨウ化物イオン(I3-)である。
測定の結果、50K(約-223℃)以上の広い温度領域で、1層あたりの電気抵抗率がおおむね量子抵抗標準値を保ったまま温度変化を示さず(図3A)、伝導層に平行に磁場を加えたときの磁化率はほぼ温度に比例しました(図3B上)。この方向の磁化率は、電子スピンの磁場の方向への偏極(ある特定の方向に偏ること)に由来する常磁性[10]ですが、観測された温度依存性はこの物質がディラック電子系であることを強く示しており、バンド計算の結果とも一致しました。
一方、伝導層に垂直方向の磁化率は極端に抑制されることを発見しました。これは、垂直方向にだけ負符号の磁化率成分である巨大な軌道反磁性が存在することを示しており、理論計算との定量的比較に堪えられる高精度の測定に成功しました(図3B下)。観測された反磁性は50K以上で温度に反比例し、温度に依存しないディラック電子系以外の反磁性とは大きく異なっていました。
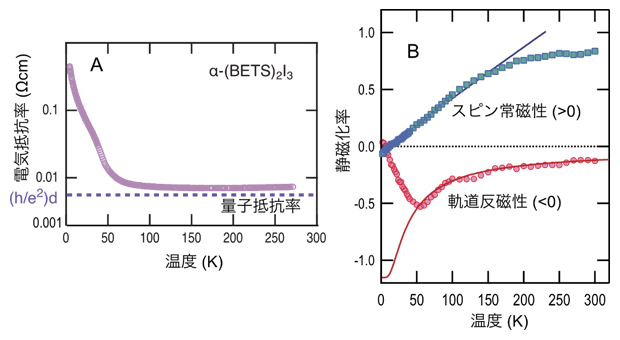
図3 α-(BETS)2I3の電磁応答
A:二次元層内の電気抵抗率(電場応答)。破線は1層あたりの量子抵抗の値を示す。
B:磁化率の角度依存性から導いた磁場応答。スピン常磁性(正の値、青)と軌道反磁性磁化率(負の値、赤)。実線は、それぞれ小さなエネルギーギャップ(50K)のときに理論的に計算される磁化率。
さらに、観測された軌道反磁性と温度の積と、電気伝導率(電気抵抗の逆数)が単純な比例関係(スケーリング則)にあることを発見しました(図4)。これまでディラック電子系では、1層あたり電気抵抗率がおおよそ量子化された値(=1)となることは知られていましたが、今回の結果は軌道反磁性にも量子化の効果が現れることを意味しています。
この磁性と電気伝導の強い関係は、ゼロギャップディラック電子分散関係と光の分散関係が同等であることに由来し、特殊相対性理論が導く時間と空間の対称性に対応していると考えられます。
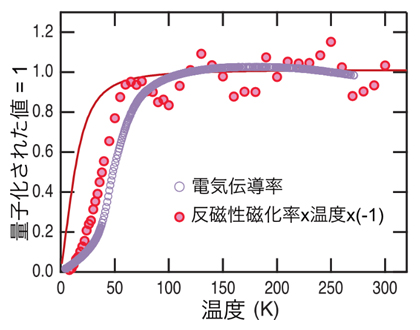
図4 電気伝導率と反磁性磁化率のスケーリング
実線は、理論から得られた反磁性磁化率に温度を乗じたもの。
一般的に固体中電子では、相対論効果である電磁応答の対称性は失われ、独立の応答を示します。しかし、ディラック電子系という特殊な物質では、特殊相対性理論における時間と空間の対称性に対応して、電場応答と磁場応答を本質的に一つのものと見なすことができます。
この研究では、グラフェンやトポロジカル絶縁体の表面状態のようなフィルム形状の物質と異なり、分子性固体という純良単結晶として存在するディラック電子系を用いて実験することで、電磁応答の対称性という本質的な性質が固体中でも観測可能になりました。
今後の期待
二次元ディラック系はグラフェンやトポロジカル絶縁体の表面状態など、近年注目されている物質に数多く存在します。本研究はディラック電子系の電磁応答について最も単純な理論から議論しているため、観測された電場応答と磁場応答の対称性は普遍的な性質であるといえます。
これらの物質では、巨大熱電応答などの新機能が理論的にも予言されており、デバイスの省エネルギー化などへの応用も期待できます。
補足説明
1.ディラック電子系
固体中電子の運動は電子分散で記述されるが、波数の1次の関数として励起エネルギーを表現できる二つの分散がX字状に交差する(エネルギーギャップがゼロの場合)か、それに漸近する双曲線関数に従う(小さいエネルギーギャップがある場合)電子状態を持つ物質を「ディラック電子系」という。
2.磁化率
物質に磁場をかけたとき、外部磁場に対してどれだけ大きな磁化(物質中の全ての磁気モーメントの足し算)を示すかを表した物理量。
3.スケーリング則
一般的には細かいパラメータによらず、いくつかの物理量が同じ関数形に従うことだが、ここでは特に、物理量の単位が異なるなど一見すると全く異なる観測量の間の単純な比例関係を指す。
4.特殊相対性理論
電磁気学の基礎方程式であるマックスウェル方程式は、自然に電場と磁場の対称性や、光が電磁波であることを導く。アインシュタインはこれらを受け、1905年に光速度不変の原理を導入し、時間と空間の統一を含む特殊相対性理論を構築した。
5.時間と空間の対称性、相対論効果
ニュートン力学では時間と空間は独立しているが、これは自転する地球上でどの方向に測定しても光が等しい速度で進む実験事実と矛盾する。光速度不変の法則を満たすためには時間と空間が同時に伸縮する必要があり、これを「時間と空間の対称性」という。またこの対称性があらわになる様子を「相対論効果」という。
6.グラフェン
グラファイトは炭素だけから成る蜂の巣状の層状物質で、鉛筆の芯として使われている。この層から1枚だけ取り出したものをグラフェンと呼び、グラフェン上の電子の運動はエネルギーギャップがゼロのディラック方程式に従う。
7.トポロジカル絶縁体
物質中の電子状態の幾何学的性質(トポロジー)を反映して、中身は電気を通さない絶縁体であるが、表面では電気を通す金属となる特殊な物質のこと。
8.α-(BETS)2I3
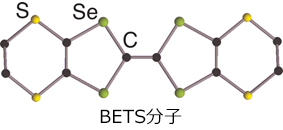
有機導体の一つで、有機分子BETS(bis(ethylenedithio)tetraselenafulvalene、下図)が並んだ層とI3-(三ヨウ化物イオン)が並んだ層とが交互に積層した層状の結晶構造をとる。I3-は閉殻であるために、I3-層は絶縁層である。一方、BETS分子は+1/2価の陽イオンになって正孔ができていることから、BETS層が電磁応答を決定づける。このようにして二次元電子系が形成されている。ギリシャ文字αはBETS分子の配列の様式を表し、他にβ、θ、κ-型などがよく知られている。
9.バンド計算、電子の分散、バンド構造
固体中の電子は波の進行として運動することから、電子の励起は波数(波長の逆数)に対するエネルギーの関数として表現される。これを「電子の分散」という。固体中では多数の電子分散が生じるが、これらを総称して「バンド構造」といい、これを求める計算を「バンド計算」という。
10.軌道反磁性、常磁性、反磁性
磁性(磁石の性質)は外部から磁場を加えたときに働く力の方向で区別される。加えた磁場と同じ向きに弱く力が働く磁性を「常磁性」といい、多くの物質で観測される。また磁場と反対方向に力が働く磁性を「反磁性」という。反磁性は水、ダイヤモンドなど身近な物質にもあるが、一般に大きさがとても小さく観測が難しい。電子の軌道運動は反磁性を作り、これを「軌道反磁性」という。古くからよく知られた軌道反磁性はラーモア反磁性だが、これは温度に依存しない。ディラック電子系において、大きい反磁性が生じることは福山秀敏、久保亮五により理論的に解明され、三次元ディラック電子系であるビスマスの反磁性(超伝導を除き自然界で最大の反磁性を示す)をよく説明している。
11.光の分散関係、光円錐
真空中の光は全ての方向に常に唯一の速度で進行するため、進んだ距離は光速度と時間の積となり、図1Bの円錐面上にしか存在しない。これを「光円錐」という。一方、光は電磁波の一つであるため、運動は波の方程式で記述できる。波は振動数(エネルギー)と波数で記述され、2量の関係を分散関係という。光の場合、振動数は光速度と波数の積となり、質量ゼロのディラック電子系の電子分散と等価となる。電子の質量が有限の場合、ディラック電子系の電子分散は金属中を伝わる電磁波の分散関係と同じ形になる。
12.フェルミ準位
固体中に多数ある電子は、電子分散のエネルギーが低い順番に充填される。このとき、最後に充填される電子のエネルギーをフェルミ準位という。固体物質の性質の多くは、フェルミ準位近傍の電子分散の形状だけに依存する。
13.ディラック方程式
電子などの微視的粒子の振る舞いを記述する量子力学に特殊相対性理論の効果を取り入れた相対論的量子力学の基礎方程式。ディラック方程式は、粒子が光速に近い速さで運動し、相対論効果が無視できなくなる高エネルギー領域において有効である。
14.核磁気共鳴(NMR)法
原子核に磁場をかけると歳差運動(すりこぎ運動)をする。この回転周期と同じ周期の交流電波を与えると原子核の信号を得ることができ、これを核磁気共鳴法という。歳差運動は原子核の周りの電子の影響を強く受けるため、実際には電子の状態を調べていることになる。医療診断に用いられるMRI(磁気共鳴画像)診断も核磁気共鳴を利用している。NMRはNuclear Magnetic Resonanceの略。
15.X線結晶構造解析
対象とする分子などの結晶を作製し、その結晶にX線を照射して得られる回折データを解析することにより、結晶内部の原子の立体的な配置を調べる方法。
共同研究グループ
理化学研究所 開拓研究本部 加藤分子物性研究室
専任研究員(研究当時) 藤山 茂樹(ふじやま しげき)
(現 岩崎中間子科学研究室 専任研究員)
主任研究員(研究当時) 加藤 礼三(かとう れいぞう)
(現 理研 研究政策審議役)
研究員(研究当時) 崔 亨波(さい きょうは)
(現 ソウル大学)
東京大学 大学院理学系研究科 物理学専攻
特任研究員 前橋 英明(まえばし ひであき)
教授 小形 正男(おがた まさお)
東邦大学 理学部 物理学科
教授 田嶋 尚也(たじま なおや)
熊本大学大学院先導機構
助教 圓谷 隆夫(つむらや たかお)
研究支援
本研究は、日本学術振興会(JSPS)科学研究費補助金基盤研究(C)「多軌道モット有機導体の作る新電子相とスピン輸送(研究代表者:藤山茂樹)」、同基盤研究(S)「分子性強相関電子系における量子液体の探索と理解(研究代表者:加藤礼三)」、同基盤研究(C)「ディラック電子系における電磁双対性の理論とその検証(研究代表者:前橋英明)」、同基盤研究(C)「物質中の量子電磁力学:ディラック電子系・ワイルフェルミオン系物質の動的応答(研究代表者:前橋英明)」、同基盤研究(B)「磁気応答、輸送現象に対する多バンド間効果(研究代表者:小形正男)」、同挑戦的研究(萌芽)「複雑分子系の有効モデル化と量子ダイナミクスの理論(研究代表者:妹尾仁嗣)」による支援を受けて行われました。
原論文情報
S. Fujiyama, H. Maebashi, N. Tajima, T. Tsumuraya, H-B. Cui, M. Ogata,and R. Kato, “Large Diamagnetism and Electromagnetic Duality in Two-Dimensional Dirac Electron System”, Physical Review Letters, 10.1103/PhysRevLett.128.027201
発表者
理化学研究所
開拓研究本部 加藤分子物性研究室
専任研究員(研究当時) 藤山 茂樹(ふじやま しげき)
(現 岩崎中間子科学研究室 専任研究員)
主任研究員(研究当時) 加藤 礼三(かとう れいぞう)
(現 理研 研究政策審議役)
東京大学 大学院理学系研究科 物理学専攻
特任研究員 前橋 英明(まえばし ひであき)
東邦大学 理学部 物理学科
教授 田嶋 尚也(たじま なおや)
報道担当
理化学研究所 広報室 報道担当
東京大学大学院理学系研究科・理学部 広報室
学校法人東邦大学 法人本部経営企画部