2019-10-23 Frank Arute,Kunal Arya,[…]John M. Martinis
量子コンピューターの約束は、特定の計算タスクが、従来のプロセッサーよりも量子プロセッサーで指数関数的に高速に実行される可能性があることです1。基本的な課題は、指数関数的に大きな計算空間で量子アルゴリズムを実行できる高忠実度のプロセッサを構築することです。ここでは、プログラム可能な超伝導量子ビット2,3,4,5,6,7を備えたプロセッサを使用して、次元253の計算状態空間(約1016)に対応する53量子ビットの量子状態を作成することを報告します。繰り返される実験からの測定は、結果の確率分布をサンプリングします。これは、古典的なシミュレーションを使用して検証します。当社のシカモアプロセッサは、量子回路の1つのインスタンスを100万回サンプリングするのに約200秒かかります。現在のベンチマークでは、最先端の古典的なスーパーコンピューターの同等のタスクには約10,000年かかることが示されています。すべての既知の古典的なアルゴリズムと比較したこの劇的な速度の向上は、この特定の計算タスクに対する量子優位性の実験的実現であり、待望のコンピューティングパラダイムの先駆けとなります。
23 October 2019
Quantum supremacy using a programmable superconducting processor
Frank Arute,Kunal Arya,[…]John M. Martinis
Nature volume 574, pages505–510 (2019) | Cite this article
504k Accesses 2 Citations 5488 Altmetric Metricsdetails
Abstract
The promise of quantum computers is that certain computational tasks might be executed exponentially faster on a quantum processor than on a classical processor1. A fundamental challenge is to build a high-fidelity processor capable of running quantum algorithms in an exponentially large computational space. Here we report the use of a processor with programmable superconducting qubits2,3,4,5,6,7 to create quantum states on 53 qubits, corresponding to a computational state-space of dimension 253 (about 1016). Measurements from repeated experiments sample the resulting probability distribution, which we verify using classical simulations. Our Sycamore processor takes about 200 seconds to sample one instance of a quantum circuit a million times—our benchmarks currently indicate that the equivalent task for a state-of-the-art classical supercomputer would take approximately 10,000 years. This dramatic increase in speed compared to all known classical algorithms is an experimental realization of quantum supremacy8,9,10,11,12,13,14 for this specific computational task, heralding a much-anticipated computing paradigm.
Main
In the early 1980s, Richard Feynman proposed that a quantum computer would be an effective tool with which to solve problems in physics and chemistry, given that it is exponentially costly to simulate large quantum systems with classical computers1. Realizing Feynman’s vision poses substantial experimental and theoretical challenges. First, can a quantum system be engineered to perform a computation in a large enough computational (Hilbert) space and with a low enough error rate to provide a quantum speedup? Second, can we formulate a problem that is hard for a classical computer but easy for a quantum computer? By computing such a benchmark task on our superconducting qubit processor, we tackle both questions. Our experiment achieves quantum supremacy, a milestone on the path to full-scale quantum computing8,9,10,11,12,13,14.
In reaching this milestone, we show that quantum speedup is achievable in a real-world system and is not precluded by any hidden physical laws. Quantum supremacy also heralds the era of noisy intermediate-scale quantum (NISQ) technologies15. The benchmark task we demonstrate has an immediate application in generating certifiable random numbers (S. Aaronson, manuscript in preparation); other initial uses for this new computational capability may include optimization16,17, machine learning18,19,20,21, materials science and chemistry22,23,24. However, realizing the full promise of quantum computing (using Shor’s algorithm for factoring, for example) still requires technical leaps to engineer fault-tolerant logical qubits25,26,27,28,29.
To achieve quantum supremacy, we made a number of technical advances which also pave the way towards error correction. We developed fast, high-fidelity gates that can be executed simultaneously across a two-dimensional qubit array. We calibrated and benchmarked the processor at both the component and system level using a powerful new tool: cross-entropy benchmarking11. Finally, we used component-level fidelities to accurately predict the performance of the whole system, further showing that quantum information behaves as expected when scaling to large systems.
A suitable computational task
To demonstrate quantum supremacy, we compare our quantum processor against state-of-the-art classical computers in the task of sampling the output of a pseudo-random quantum circuit11,13,14. Random circuits are a suitable choice for benchmarking because they do not possess structure and therefore allow for limited guarantees of computational hardness10,11,12. We design the circuits to entangle a set of quantum bits (qubits) by repeated application of single-qubit and two-qubit logical operations. Sampling the quantum circuit’s output produces a set of bitstrings, for example {0000101, 1011100, …}. Owing to quantum interference, the probability distribution of the bitstrings resembles a speckled intensity pattern produced by light interference in laser scatter, such that some bitstrings are much more likely to occur than others. Classically computing this probability distribution becomes exponentially more difficult as the number of qubits (width) and number of gate cycles (depth) grow.
We verify that the quantum processor is working properly using a method called cross-entropy benchmarking11,12,14, which compares how often each bitstring is observed experimentally with its corresponding ideal probability computed via simulation on a classical computer. For a given circuit, we collect the measured bitstrings {xi} and compute the linear cross-entropy benchmarking fidelity11,13,14 (see also Supplementary Information), which is the mean of the simulated probabilities of the bitstrings we measured:
FXEB=2n⟨P(xi)⟩i−1<?XML:NAMESPACE PREFIX = “[default] http://www.w3.org/1998/Math/MathML” NS = “http://www.w3.org/1998/Math/MathML” />FXEB=2n⟨P(xi)⟩i−1
(1)
where n is the number of qubits, P(xi) is the probability of bitstring xi computed for the ideal quantum circuit, and the average is over the observed bitstrings. Intuitively, FXEBFXEB is correlated with how often we sample high-probability bitstrings. When there are no errors in the quantum circuit, the distribution of probabilities is exponential (see Supplementary Information), and sampling from this distribution will produce FXEB=1FXEB=1. On the other hand, sampling from the uniform distribution will give ⟨P(xi)⟩i = 1/2n and produce FXEB=0FXEB=0. Values of FXEBFXEB between 0 and 1 correspond to the probability that no error has occurred while running the circuit. The probabilities P(xi) must be obtained from classically simulating the quantum circuit, and thus computing FXEBFXEB is intractable in the regime of quantum supremacy. However, with certain circuit simplifications, we can obtain quantitative fidelity estimates of a fully operating processor running wide and deep quantum circuits.
Our goal is to achieve a high enough FXEBFXEB for a circuit with sufficient width and depth such that the classical computing cost is prohibitively large. This is a difficult task because our logic gates are imperfect and the quantum states we intend to create are sensitive to errors. A single bit or phase flip over the course of the algorithm will completely shuffle the speckle pattern and result in close to zero fidelity11 (see also Supplementary Information). Therefore, in order to claim quantum supremacy we need a quantum processor that executes the program with sufficiently low error rates.
Building a high-fidelity processor
We designed a quantum processor named ‘Sycamore’ which consists of a two-dimensional array of 54 transmon qubits, where each qubit is tunably coupled to four nearest neighbours, in a rectangular lattice. The connectivity was chosen to be forward-compatible with error correction using the surface code26. A key systems engineering advance of this device is achieving high-fidelity single- and two-qubit operations, not just in isolation but also while performing a realistic computation with simultaneous gate operations on many qubits. We discuss the highlights below; see also the Supplementary Information.
In a superconducting circuit, conduction electrons condense into a macroscopic quantum state, such that currents and voltages behave quantum mechanically2,30. Our processor uses transmon qubits6, which can be thought of as nonlinear superconducting resonators at 5–7 GHz. The qubit is encoded as the two lowest quantum eigenstates of the resonant circuit. Each transmon has two controls: a microwave drive to excite the qubit, and a magnetic flux control to tune the frequency. Each qubit is connected to a linear resonator used to read out the qubit state5. As shown in Fig. 1, each qubit is also connected to its neighbouring qubits using a new adjustable coupler31,32. Our coupler design allows us to quickly tune the qubit–qubit coupling from completely off to 40 MHz. One qubit did not function properly, so the device uses 53 qubits and 86 couplers.
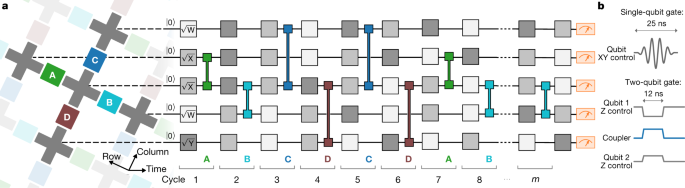
Fig. 1: The Sycamore processor.
a, Layout of processor, showing a rectangular array of 54 qubits (grey), each connected to its four nearest neighbours with couplers (blue). The inoperable qubit is outlined. b, Photograph of the Sycamore chip.
The processor is fabricated using aluminium for metallization and Josephson junctions, and indium for bump-bonds between two silicon wafers. The chip is wire-bonded to a superconducting circuit board and cooled to below 20 mK in a dilution refrigerator to reduce ambient thermal energy to well below the qubit energy. The processor is connected through filters and attenuators to room-temperature electronics, which synthesize the control signals. The state of all qubits can be read simultaneously by using a frequency-multiplexing technique33,34. We use two stages of cryogenic amplifiers to boost the signal, which is digitized (8 bits at 1 GHz) and demultiplexed digitally at room temperature. In total, we orchestrate 277 digital-to-analog converters (14 bits at 1 GHz) for complete control of the quantum processor.
We execute single-qubit gates by driving 25-ns microwave pulses resonant with the qubit frequency while the qubit–qubit coupling is turned off. The pulses are shaped to minimize transitions to higher transmon states35. Gate performance varies strongly with frequency owing to two-level-system defects36,37, stray microwave modes, coupling to control lines and the readout resonator, residual stray coupling between qubits, flux noise and pulse distortions. We therefore optimize the single-qubit operation frequencies to mitigate these error mechanisms.
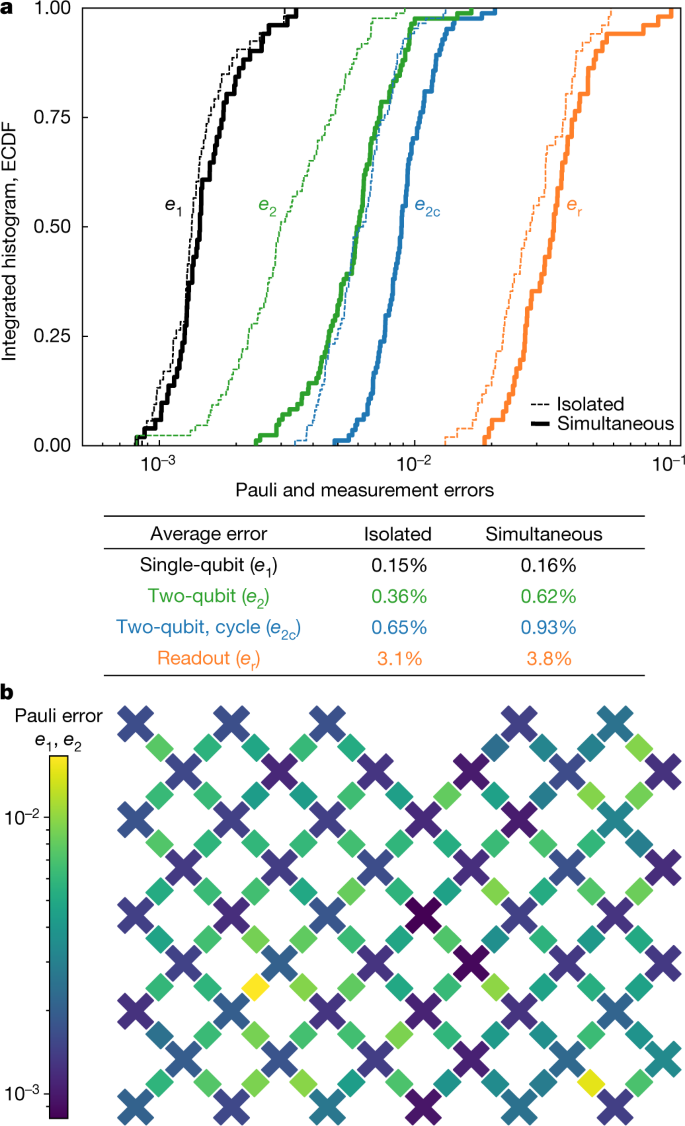
We benchmark single-qubit gate performance by using the cross-entropy benchmarking protocol described above, reduced to the single-qubit level (n = 1), to measure the probability of an error occurring during a single-qubit gate. On each qubit, we apply a variable number m of randomly selected gates and measure FXEBFXEB averaged over many sequences; as m increases, errors accumulate and average FXEBFXEB decays. We model this decay by [1 − e1/(1 − 1/D2)]m where e1 is the Pauli error probability. The state (Hilbert) space dimension term, D = 2n, which equals 2 for this case, corrects for the depolarizing model where states with errors partially overlap with the ideal state. This procedure is similar to the more typical technique of randomized benchmarking27,38,39, but supports non-Clifford-gate sets40 and can separate out decoherence error from coherent control error. We then repeat the experiment with all qubits executing single-qubit gates simultaneously (Fig. 2), which shows only a small increase in the error probabilities, demonstrating that our device has low microwave crosstalk.
Fig. 2: System-wide Pauli and measurement errors.
a, Integrated histogram (empirical cumulative distribution function, ECDF) of Pauli errors (black, green, blue) and readout errors (orange), measured on qubits in isolation (dotted lines) and when operating all qubits simultaneously (solid). The median of each distribution occurs at 0.50 on the vertical axis. Average (mean) values are shown below. b, Heat map showing single- and two-qubit Pauli errors e1 (crosses) and e2 (bars) positioned in the layout of the processor. Values are shown for all qubits operating simultaneously.
We perform two-qubit iSWAP-like entangling gates by bringing neighbouring qubits on-resonance and turning on a 20-MHz coupling for 12 ns, which allows the qubits to swap excitations. During this time, the qubits also experience a controlled-phase (CZ) interaction, which originates from the higher levels of the transmon. The two-qubit gate frequency trajectories of each pair of qubits are optimized to mitigate the same error mechanisms considered in optimizing single-qubit operation frequencies.
To characterize and benchmark the two-qubit gates, we run two-qubit circuits with m cycles, where each cycle contains a randomly chosen single-qubit gate on each of the two qubits followed by a fixed two-qubit gate. We learn the parameters of the two-qubit unitary (such as the amount of iSWAP and CZ interaction) by using FXEBFXEB as a cost function. After this optimization, we extract the per-cycle error e2c from the decay of FXEBFXEB with m, and isolate the two-qubit error e2 by subtracting the two single-qubit errors e1. We find an average e2 of 0.36%. Additionally, we repeat the same procedure while simultaneously running two-qubit circuits for the entire array. After updating the unitary parameters to account for effects such as dispersive shifts and crosstalk, we find an average e2 of 0.62%.
For the full experiment, we generate quantum circuits using the two-qubit unitaries measured for each pair during simultaneous operation, rather than a standard gate for all pairs. The typical two-qubit gate is a full iSWAP with 1/6th of a full CZ. Using individually calibrated gates in no way limits the universality of the demonstration. One can compose, for example, controlled-NOT (CNOT) gates from 1-qubit gates and two of the unique 2-qubit gates of any given pair. The implementation of high-fidelity ‘textbook gates’ natively, such as CZ or iSWAP−−−−−−√iSWAP, is work in progress.
Finally, we benchmark qubit readout using standard dispersive measurement41. Measurement errors averaged over the 0 and 1 states are shown in Fig. 2a. We have also measured the error when operating all qubits simultaneously, by randomly preparing each qubit in the 0 or 1 state and then measuring all qubits for the probability of the correct result. We find that simultaneous readout incurs only a modest increase in per-qubit measurement errors.
Having found the error rates of the individual gates and readout, we can model the fidelity of a quantum circuit as the product of the probabilities of error-free operation of all gates and measurements. Our largest random quantum circuits have 53 qubits, 1,113 single-qubit gates, 430 two-qubit gates, and a measurement on each qubit, for which we predict a total fidelity of 0.2%. This fidelity should be resolvable with a few million measurements, since the uncertainty on FXEBFXEB is 1/Ns−−√1/Ns, where Ns is the number of samples. Our model assumes that entangling larger and larger systems does not introduce additional error sources beyond the errors we measure at the single- and two-qubit level. In the next section we will see how well this hypothesis holds up.
Fidelity estimation in the supremacy regime
The gate sequence for our pseudo-random quantum circuit generation is shown in Fig. 3. One cycle of the algorithm consists of applying single-qubit gates chosen randomly from {X−−√,Y−−√,W−−√}{X,Y,W} on all qubits, followed by two-qubit gates on pairs of qubits. The sequences of gates which form the ‘supremacy circuits’ are designed to minimize the circuit depth required to create a highly entangled state, which is needed for computational complexity and classical hardness.
Fig. 3: Control operations for the quantum supremacy circuits.
a, Example quantum circuit instance used in our experiment. Every cycle includes a layer each of single- and two-qubit gates. The single-qubit gates are chosen randomly from {X−−√,Y−−√,W−−√}{X,Y,W}, where W=(X+Y)/2–√W=(X+Y)/2 and gates do not repeat sequentially. The sequence of two-qubit gates is chosen according to a tiling pattern, coupling each qubit sequentially to its four nearest-neighbour qubits. The couplers are divided into four subsets (ABCD), each of which is executed simultaneously across the entire array corresponding to shaded colours. Here we show an intractable sequence (repeat ABCDCDAB); we also use different coupler subsets along with a simplifiable sequence (repeat EFGHEFGH, not shown) that can be simulated on a classical computer. b, Waveform of control signals for single- and two-qubit gates.
Although we cannot compute FXEBFXEB in the supremacy regime, we can estimate it using three variations to reduce the complexity of the circuits. In ‘patch circuits’, we remove a slice of two-qubit gates (a small fraction of the total number of two-qubit gates), splitting the circuit into two spatially isolated, non-interacting patches of qubits. We then compute the total fidelity as the product of the patch fidelities, each of which can be easily calculated. In ‘elided circuits’, we remove only a fraction of the initial two-qubit gates along the slice, allowing for entanglement between patches, which more closely mimics the full experiment while still maintaining simulation feasibility. Finally, we can also run full ‘verification circuits’, with the same gate counts as our supremacy circuits, but with a different pattern for the sequence of two-qubit gates, which is much easier to simulate classically (see also Supplementary Information). Comparison between these three variations allows us to track the system fidelity as we approach the supremacy regime.
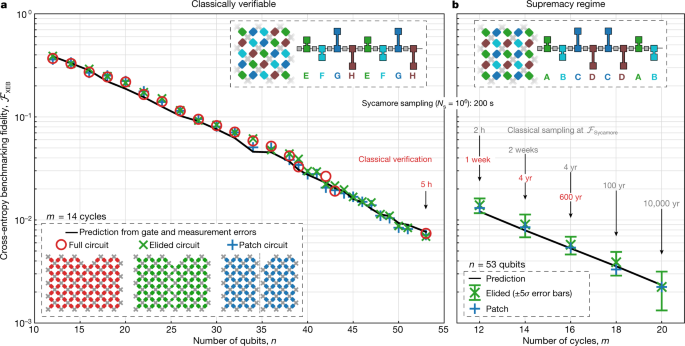
We first check that the patch and elided versions of the verification circuits produce the same fidelity as the full verification circuits up to 53 qubits, as shown in Fig. 4a. For each data point, we typically collect Ns = 5 × 106 total samples over ten circuit instances, where instances differ only in the choices of single-qubit gates in each cycle. We also show predicted FXEBFXEB values, computed by multiplying the no-error probabilities of single- and two-qubit gates and measurement (see also Supplementary Information). The predicted, patch and elided fidelities all show good agreement with the fidelities of the corresponding full circuits, despite the vast differences in computational complexity and entanglement. This gives us confidence that elided circuits can be used to accurately estimate the fidelity of more-complex circuits.
Fig. 4: Demonstrating quantum supremacy.
a, Verification of benchmarking methods. FXEBFXEB values for patch, elided and full verification circuits are calculated from measured bitstrings and the corresponding probabilities predicted by classical simulation. Here, the two-qubit gates are applied in a simplifiable tiling and sequence such that the full circuits can be simulated out to n = 53, m = 14 in a reasonable amount of time. Each data point is an average over ten distinct quantum circuit instances that differ in their single-qubit gates (for n = 39, 42 and 43 only two instances were simulated). For each n, each instance is sampled with Ns of 0.5–2.5 million. The black line shows the predicted FXEBFXEB based on single- and two-qubit gate and measurement errors. The close correspondence between all four curves, despite their vast differences in complexity, justifies the use of elided circuits to estimate fidelity in the supremacy regime. b, Estimating FXEBFXEB in the quantum supremacy regime. Here, the two-qubit gates are applied in a non-simplifiable tiling and sequence for which it is much harder to simulate. For the largest elided data (n = 53, m = 20, total Ns = 30 million), we find an average FXEBFXEB > 0.1% with 5σ confidence, where σ includes both systematic and statistical uncertainties. The corresponding full circuit data, not simulated but archived, is expected to show similarly statistically significant fidelity. For m = 20, obtaining a million samples on the quantum processor takes 200 seconds, whereas an equal-fidelity classical sampling would take 10,000 years on a million cores, and verifying the fidelity would take millions of years.
The largest circuits for which the fidelity can still be directly verified have 53 qubits and a simplified gate arrangement. Performing random circuit sampling on these at 0.8% fidelity takes one million cores 130 seconds, corresponding to a million-fold speedup of the quantum processor relative to a single core.
We proceed now to benchmark our computationally most difficult circuits, which are simply a rearrangement of the two-qubit gates. In Fig. 4b, we show the measured FXEBFXEB for 53-qubit patch and elided versions of the full supremacy circuits with increasing depth. For the largest circuit with 53 qubits and 20 cycles, we collected Ns = 30 × 106 samples over ten circuit instances, obtaining FXEB=(2.24±0.21)×10−3FXEB=(2.24±0.21)×10−3 for the elided circuits. With 5σ confidence, we assert that the average fidelity of running these circuits on the quantum processor is greater than at least 0.1%. We expect that the full data for Fig. 4b should have similar fidelities, but since the simulation times (red numbers) take too long to check, we have archived the data (see ‘Data availability’ section). The data is thus in the quantum supremacy regime.
The classical computational cost
We simulate the quantum circuits used in the experiment on classical computers for two purposes: (1) verifying our quantum processor and benchmarking methods by computing FXEBFXEB where possible using simplifiable circuits (Fig. 4a), and (2) estimating FXEBFXEB as well as the classical cost of sampling our hardest circuits (Fig. 4b). Up to 43 qubits, we use a Schrödinger algorithm, which simulates the evolution of the full quantum state; the Jülich supercomputer (with 100,000 cores, 250 terabytes) runs the largest cases. Above this size, there is not enough random access memory (RAM) to store the quantum state42. For larger qubit numbers, we use a hybrid Schrödinger–Feynman algorithm43 running on Google data centres to compute the amplitudes of individual bitstrings. This algorithm breaks the circuit up into two patches of qubits and efficiently simulates each patch using a Schrödinger method, before connecting them using an approach reminiscent of the Feynman path-integral. Although it is more memory-efficient, the Schrödinger–Feynman algorithm becomes exponentially more computationally expensive with increasing circuit depth owing to the exponential growth of paths with the number of gates connecting the patches.
To estimate the classical computational cost of the supremacy circuits (grey numbers in Fig. 4b), we ran portions of the quantum circuit simulation on both the Summit supercomputer as well as on Google clusters and extrapolated to the full cost. In this extrapolation, we account for the computation cost of sampling by scaling the verification cost with FXEBFXEB, for example43,44, a 0.1% fidelity decreases the cost by about 1,000. On the Summit supercomputer, which is currently the most powerful in the world, we used a method inspired by Feynman path-integrals that is most efficient at low depth44,45,46,47. At m = 20 the tensors do not reasonably fit into node memory, so we can only measure runtimes up to m = 14, for which we estimate that sampling three million bitstrings with 1% fidelity would require a year.
On Google Cloud servers, we estimate that performing the same task for m = 20 with 0.1% fidelity using the Schrödinger–Feynman algorithm would cost 50 trillion core-hours and consume one petawatt hour of energy. To put this in perspective, it took 600 seconds to sample the circuit on the quantum processor three million times, where sampling time is limited by control hardware communications; in fact, the net quantum processor time is only about 30 seconds. The bitstring samples from all circuits have been archived online (see ‘Data availability’ section) to encourage development and testing of more advanced verification algorithms.
One may wonder to what extent algorithmic innovation can enhance classical simulations. Our assumption, based on insights from complexity theory11,12,13, is that the cost of this algorithmic task is exponential in circuit size. Indeed, simulation methods have improved steadily over the past few years42,43,44,45,46,47,48,49,50. We expect that lower simulation costs than reported here will eventually be achieved, but we also expect that they will be consistently outpaced by hardware improvements on larger quantum processors.
Verifying the digital error model
A key assumption underlying the theory of quantum error correction is that quantum state errors may be considered digitized and localized38,51. Under such a digital model, all errors in the evolving quantum state may be characterized by a set of localized Pauli errors (bit-flips or phase-flips) interspersed into the circuit. Since continuous amplitudes are fundamental to quantum mechanics, it needs to be tested whether errors in a quantum system could be treated as discrete and probabilistic. Indeed, our experimental observations support the validity of this model for our processor. Our system fidelity is well predicted by a simple model in which the individually characterized fidelities of each gate are multiplied together (Fig. 4).
To be successfully described by a digitized error model, a system should be low in correlated errors. We achieve this in our experiment by choosing circuits that randomize and decorrelate errors, by optimizing control to minimize systematic errors and leakage, and by designing gates that operate much faster than correlated noise sources, such as 1/f flux noise37. Demonstrating a predictive uncorrelated error model up to a Hilbert space of size 253 shows that we can build a system where quantum resources, such as entanglement, are not prohibitively fragile.
The future
Quantum processors based on superconducting qubits can now perform computations in a Hilbert space of dimension 253 ≈ 9 × 1015, beyond the reach of the fastest classical supercomputers available today. To our knowledge, this experiment marks the first computation that can be performed only on a quantum processor. Quantum processors have thus reached the regime of quantum supremacy. We expect that their computational power will continue to grow at a double-exponential rate: the classical cost of simulating a quantum circuit increases exponentially with computational volume, and hardware improvements will probably follow a quantum-processor equivalent of Moore’s law52,53, doubling this computational volume every few years. To sustain the double-exponential growth rate and to eventually offer the computational volume needed to run well known quantum algorithms, such as the Shor or Grover algorithms25,54, the engineering of quantum error correction will need to become a focus of attention.
The extended Church–Turing thesis formulated by Bernstein and Vazirani55 asserts that any ‘reasonable’ model of computation can be efficiently simulated by a Turing machine. Our experiment suggests that a model of computation may now be available that violates this assertion. We have performed random quantum circuit sampling in polynomial time using a physically realizable quantum processor (with sufficiently low error rates), yet no efficient method is known to exist for classical computing machinery. As a result of these developments, quantum computing is transitioning from a research topic to a technology that unlocks new computational capabilities. We are only one creative algorithm away from valuable near-term applications.
Data availability
The datasets generated and analysed for this study are available at our public Dryad repository (https://doi.org/10.5061/dryad.k6t1rj8).
References
- Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
- Devoret, M. H., Martinis, J. M. & Clarke, J. Measurements of macroscopic quantum tunneling out of the zero-voltage state of a current-biased Josephson junction. Phys. Rev. Lett. 55, 1908 (1985).
- Nakamura, Y., Chen, C. D. & Tsai, J. S. Spectroscopy of energy-level splitting between two macroscopic quantum states of charge coherently superposed by Josephson coupling. Phys. Rev. Lett. 79, 2328 (1997).
-
Mooij, J. et al. Josephson persistent-current qubit. Science 285, 1036–1039 (1999).
-
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
-
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
- You, J. Q. & Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 474, 589–597 (2011).
- Preskill, J. Quantum computing and the entanglement frontier. Rapporteur Talk at the 25th Solvay Conference on Physics, Brussels https://doi.org/10.1142/8674 (World Scientific, 2012).
- Aaronson, S. & Arkhipov, A. The computational complexity of linear optics. In Proc. 43rd Ann. Symp. on Theory of Computing https://doi.org/10.1145/1993636.1993682 (ACM, 2011).
- Bremner, M. J., Montanaro, A. & Shepherd, D. J. Average-case complexity versus approximate simulation of commuting quantum computations. Phys. Rev. Lett. 117, 080501 (2016).
- Boixo, S. et al. Characterizing quantum supremacy in near-term devices. Nat. Phys. 14, 595 (2018).
- Bouland, A., Fefferman, B., Nirkhe, C. & Vazirani, U. On the complexity and verification of quantum random circuit sampling. Nat. Phys. 15, 159 (2019).
- Aaronson, S. & Chen, L. Complexity-theoretic foundations of quantum supremacy experiments. In 32nd Computational Complexity Conf. https://doi.org/10.4230/LIPIcs.CCC.2017.22 (Schloss Dagstuhl–Leibniz Zentrum für Informatik, 2017).
- Neill, C. et al. A blueprint for demonstrating quantum supremacy with superconducting qubits. Science 360, 195–199 (2018).
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018).
- Kechedzhi, K. et al. Efficient population transfer via non-ergodic extended states in quantum spin glass. In 13th Conf. on the Theory of Quantum Computation, Communication and Cryptography http://drops.dagstuhl.de/opus/volltexte/2018/9256/pdf/LIPIcs-TQC-2018-9.pdf (Schloss Dagstuhl–Leibniz Zentrum für Informatik, 2018).
- Somma, R. D., Boixo, S., Barnum, H. & Knill, E. Quantum simulations of classical annealing processes. Phys. Rev. Lett. 101, 130504 (2008).
- Farhi, E. & Neven, H. Classification with quantum neural networks on near term processors. Preprint at https://arxiv.org/abs/1802.06002 (2018).
- McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 9, 4812 (2018).
- Cong, I., Choi, S. & Lukin, M. D. Quantum convolutional neural networks. Nat. Phys. https://doi.org/10.1038/s41567-019-0648-8 (2019).
- Bravyi, S., Gosset, D. & König, R. Quantum advantage with shallow circuits. Science 362, 308–311 (2018).
- Aspuru-Guzik, A., Dutoi, A. D., Love, P. J. & Head-Gordon, M. Simulated quantum computation of molecular energies. Science 309, 1704–1707 (2005).
- Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).
- Hempel, C. et al. Quantum chemistry calculations on a trapped-ion quantum simulator. Phys. Rev. X 8, 031022 (2018).
- Shor, P. W. Algorithms for quantum computation: discrete logarithms and factoring proceedings. In Proc. 35th Ann. Symp. on Foundations of Computer Science https://doi.org/10.1109/SFCS.1994.365700 (IEEE, 1994).
- Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
- Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503 (2014).
- Córcoles, A. D. et al. Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 6, 6979 (2015).
- Ofek, N. et al. Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 536, 441 (2016).
- Vool, U. & Devoret, M. Introduction to quantum electromagnetic circuits. Int. J. Circuit Theory Appl. 45, 897–934 (2017).
- Chen, Y. et al. Qubit architecture with high coherence and fast tunable coupling circuits. Phys. Rev. Lett. 113, 220502 (2014).
- Yan, F. et al. A tunable coupling scheme for implementing high-fidelity two-qubit gates. Phys. Rev. Appl. 10, 054062 (2018).
- Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515 (2007).
- Jeffrey, E. et al. Fast accurate state measurement with superconducting qubits. Phys. Rev. Lett. 112, 190504 (2014).
- Chen, Z. et al. Measuring and suppressing quantum state leakage in a superconducting qubit. Phys. Rev. Lett. 116, 020501 (2016).
- Klimov, P. V. et al. Fluctuations of energy-relaxation times in superconducting qubits. Phys. Rev. Lett. 121, 090502 (2018).
- Yan, F. et al. The flux qubit revisited to enhance coherence and reproducibility. Nat. Commun. 7, 12964 (2016).
- Knill, E. et al. Randomized benchmarking of quantum gates. Phys. Rev. A 77, 012307 (2008).
- Magesan, E., Gambetta, J. M. & Emerson, J. Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett. 106, 180504 (2011).
- Cross, A. W., Magesan, E., Bishop, L. S., Smolin, J. A. & Gambetta, J. M. Scalable randomised benchmarking of non-Clifford gates. npj Quant. Inform. 2, 16012 (2016).
- Wallraff, A. et al. Approaching unit visibility for control of a superconducting qubit with dispersive readout. Phys. Rev. Lett. 95, 060501 (2005).
- De Raedt, H. et al. Massively parallel quantum computer simulator, eleven years later. Comput. Phys. Commun. 237, 47–61 (2019).
- Markov, I. L., Fatima, A., Isakov, S. V. & Boixo, S. Quantum supremacy is both closer and farther than it appears. Preprint at https://arxiv.org/abs/1807.10749 (2018).
- Villalonga, B. et al. A flexible high-performance simulator for the verification and benchmarking of quantum circuits implemented on real hardware. npj Quant. Inform. (in the press); preprint at https://arxiv.org/abs/1811.09599 (2018).
- Boixo, S., Isakov, S. V., Smelyanskiy, V. N. & Neven, H. Simulation of low-depth quantum circuits as complex undirected graphical models. Preprint at https://arxiv.org/abs/1712.05384 (2017).
- Chen, J., Zhang, F., Huang, C., Newman, M. & Shi, Y. Classical simulation of intermediate-size quantum circuits. Preprint at https://arxiv.org/abs/1805.01450 (2018).
- Villalonga, B. et al. Establishing the quantum supremacy frontier with a 281 pflop/s simulation. Preprint at https://arxiv.org/abs/1905.00444 (2019).
- Pednault, E. et al. Breaking the 49-qubit barrier in the simulation of quantum circuits. Preprint at https://arxiv.org/abs/1710.05867 (2017).
- Chen, Z. Y. et al. 64-qubit quantum circuit simulation. Sci. Bull. 63, 964–971 (2018).
- Chen, M.-C. et al. Quantum-teleportation-inspired algorithm for sampling large random quantum circuits. Preprint at https://arxiv.org/abs/1901.05003 (2019).
- Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493–R2496 (1995).
- Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013).
- Mohseni, M. et al. Commercialize quantum technologies in five years. Nature 543, 171 (2017).
- Grover, L. K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79, 325 (1997).
- Bernstein, E. & Vazirani, U. Quantum complexity theory. In Proc. 25th Ann. Symp. on Theory of Computing https://doi.org/10.1145/167088.167097 (ACM, 1993).
Acknowledgements
We are grateful to E. Schmidt, S. Brin, S. Pichai, J. Dean, J. Yagnik and J. Giannandrea for their executive sponsorship of the Google AI Quantum team, and for their continued engagement and support. We thank P. Norvig, J. Yagnik, U. Hölzle and S. Pichai for advice on the manuscript. We acknowledge K. Kissel, J. Raso, D. L. Yonge-Mallo, O. Martin and N. Sridhar for their help with simulations. We thank G. Bortoli and L. Laws for keeping our team organized. This research used resources from the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility (supported by contract DE-AC05-00OR22725). A portion of this work was performed in the UCSB Nanofabrication Facility, an open access laboratory. R.B., S.M., and E.G.R. appreciate support from the NASA Ames Research Center and from the Air Force Research (AFRL) Information Directorate (grant F4HBKC4162G001). T.S.H. is supported by the DOE Early Career Research Program. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of AFRL or the US government.
Author information
Affiliations
Google AI Quantum, Mountain View, CA, USA
Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C. Bardin
, Rami Barends, Sergio Boixo, Fernando G. S. L. Brandao, David A. Buell
, Brian Burkett, Yu Chen, Zijun Chen, Roberto Collins, William Courtney
, Andrew Dunsworth, Edward Farhi, Brooks Foxen, Austin Fowler
, Craig Gidney, Marissa Giustina, Rob Graff, Keith Guerin
, Steve Habegger, Matthew P. Harrigan, Michael J. Hartmann, Alan Ho
, Markus Hoffmann, Trent Huang, Sergei V. Isakov, Evan Jeffrey
, Zhang Jiang, Dvir Kafri, Kostyantyn Kechedzhi, Julian Kelly
, Paul V. Klimov, Sergey Knysh, Alexander Korotkov, Fedor Kostritsa
, David Landhuis, Mike Lindmark, Erik Lucero, Jarrod R. McClean
, Anthony Megrant, Xiao Mi, Masoud Mohseni, Josh Mutus
, Ofer Naaman, Matthew Neeley, Charles Neill, Murphy Yuezhen Niu
, Eric Ostby, Andre Petukhov, John C. Platt, Chris Quintana
, Pedram Roushan, Nicholas C. Rubin, Daniel Sank, Kevin J. Satzinger
, Vadim Smelyanskiy, Kevin J. Sung, Matthew D. Trevithick, Amit Vainsencher
, Benjamin Villalonga, Theodore White, Z. Jamie Yao, Ping Yeh
, Adam Zalcman, Hartmut Neven & John M. Martinis
Department of Electrical and Computer Engineering, University of Massachusetts Amherst, Amherst, MA, USA
-
- Joseph C. Bardin
Quantum Artificial Intelligence Laboratory (QuAIL), NASA Ames Research Center, Moffett Field, CA, USA
-
- Rupak Biswas
- , Salvatore Mandrà
- & Eleanor G. Rieffel
Institute for Quantum Information and Matter, Caltech, Pasadena, CA, USA
-
- Fernando G. S. L. Brandao
-
Department of Physics, University of California, Santa Barbara, CA, USA
- Ben Chiaro
- , Brooks Foxen
- , Matthew McEwen
- & John M. Martinis
-
Friedrich-Alexander University Erlangen-Nürnberg (FAU), Department of Physics, Erlangen, Germany
- Michael J. Hartmann
-
Quantum Computing Institute, Oak Ridge National Laboratory, Oak Ridge, TN, USA
- Travis S. Humble
-
Department of Electrical and Computer Engineering, University of California, Riverside, CA, USA
- Alexander Korotkov
-
Scientific Computing, Oak Ridge Leadership Computing, Oak Ridge National Laboratory, Oak Ridge, TN, USA
- Dmitry Lyakh
-
Stinger Ghaffarian Technologies Inc., Greenbelt, MD, USA
- Salvatore Mandrà
-
Institute for Advanced Simulation, Jülich Supercomputing Centre, Forschungszentrum Jülich, Jülich, Germany
- Kristel Michielsen
-
RWTH Aachen University, Aachen, Germany
- Kristel Michielsen
-
Department of Electrical Engineering and Computer Science, University of Michigan, Ann Arbor, MI, USA
- Kevin J. Sung
-
Department of Physics, University of Illinois at Urbana-Champaign, Urbana, IL, USA
- Benjamin Villalonga
Contributions
The Google AI Quantum team conceived the experiment. The applications and algorithms team provided the theoretical foundation and the specifics of the algorithm. The hardware team carried out the experiment and collected the data. The data analysis was done jointly with outside collaborators. All authors wrote and revised the manuscript and the Supplementary Information.
Corresponding author
Correspondence to John M. Martinis.
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Scott Aaronson, Keisuke Fujii and William Oliver for their contribution to the peer review of this work.
Supplementary information
Supplementary Information
This file contains Supplementary Information I–XI, which contains supplementary figures S1–S44 and Supplementary Tables I–X