2022-10-05 東京大学
図司 陽平(理学専攻 博士課程2年)
竹内 一将(物理学専攻 准教授)
発表のポイント
- 液晶中のトポロジカルな「ひも」である線欠陥の3次元運動を、欠陥の直接蛍光イメージングにより初めて観測した。
- 「ひも」同士がつなぎ替わる再結合という現象に着目し、3次元トポロジカル欠陥に特徴的な運動の様子を明らかにし、そのメカニズムを議論した。
- トポロジカル欠陥は、宇宙論や超流動、生物など様々な科学分野に現れ重要な役割を果たしているため、その普遍的な性質を明らかにすることは液晶だけにとどまらない意義がある。
発表概要
指紋を眺めてみよう。おおよそ同じ方向に筋が走っているが、ところどころ渦巻や枝分かれ、馬蹄形など向きが揃わない場所がある(図1)。

図1:指紋に見られるトポロジカル欠陥。「+1/2欠陥」と「-1/2欠陥」の2種類が観察できる。指紋の写真は Wikimedia Commons より(パブリックドメイン)。
そのような場所は、トポロジー(注1)に起源を持つため、トポロジカル欠陥と呼ばれる。同じように、細長い分子同士が互いに向きを揃えようとする液晶中でもトポロジカル欠陥がみられる。液晶で見られる「ひも」状のトポロジカル欠陥は、ジェットコースターのレールのように3次元的に曲がりくねったり、相互作用して動き回ったりする(図2)。このようトポロジカル欠陥のふるまいは、理学・工学両面から興味を持たれてきたが、その3次元構造を直接観測することは容易ではなかった。
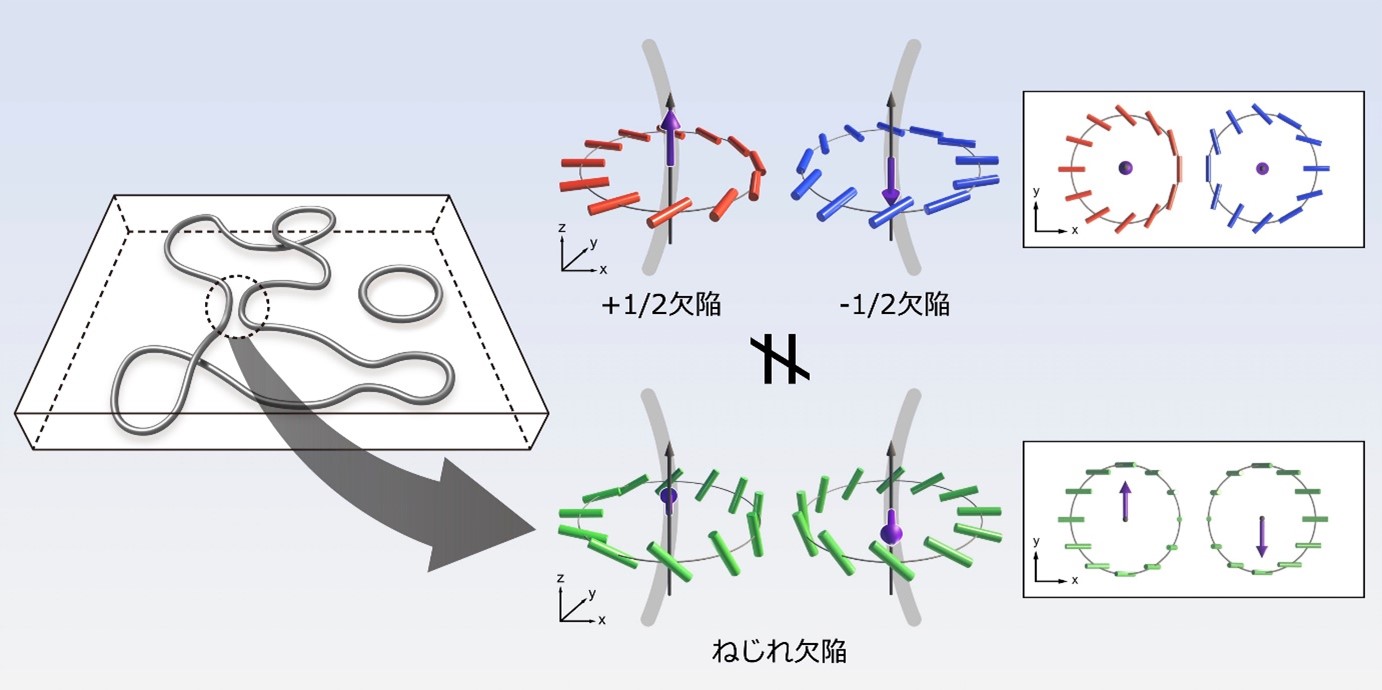
図2:トポロジカルな線欠陥とその構造を表す概念図。実験で観察される線欠陥の中には、今にもつなぎ替えを起こそうとしているものもある(図左、破線部分)。このつなぎ替え現象(再結合)の運動解析の結果、こうした線欠陥では「ねじれ欠陥」と呼ばれる構造(図右下)が自然に生じており、2次元液晶で見られる±1/2欠陥(図右上)とは異なることが判明した。
東京大学大学院理学系研究科の図司陽平大学院生と竹内一将准教授は、静止した欠陥への蛍光色素の集積現象を運動観察に応用できることを見出し、トポロジカル欠陥の動きを3次元で捉えることに成功した(動画1- 3)。特に、トポロジカル欠陥同士がぶつかってつなぎ替わる再結合と呼ばれる現象(図3上)に着目し、運動の様子を解析した。トポロジカル欠陥は液晶以外の研究領域にも広く現れる概念であり、今回の研究は分野を超えてトポロジカル欠陥の理解を深めることにつながると期待される。
動画1:トポロジカルな線欠陥の3次元運動(約3倍速再生)
動画2:トポロジカル欠陥の再結合
動画3:トポロジカル欠陥ループの縮小・消滅
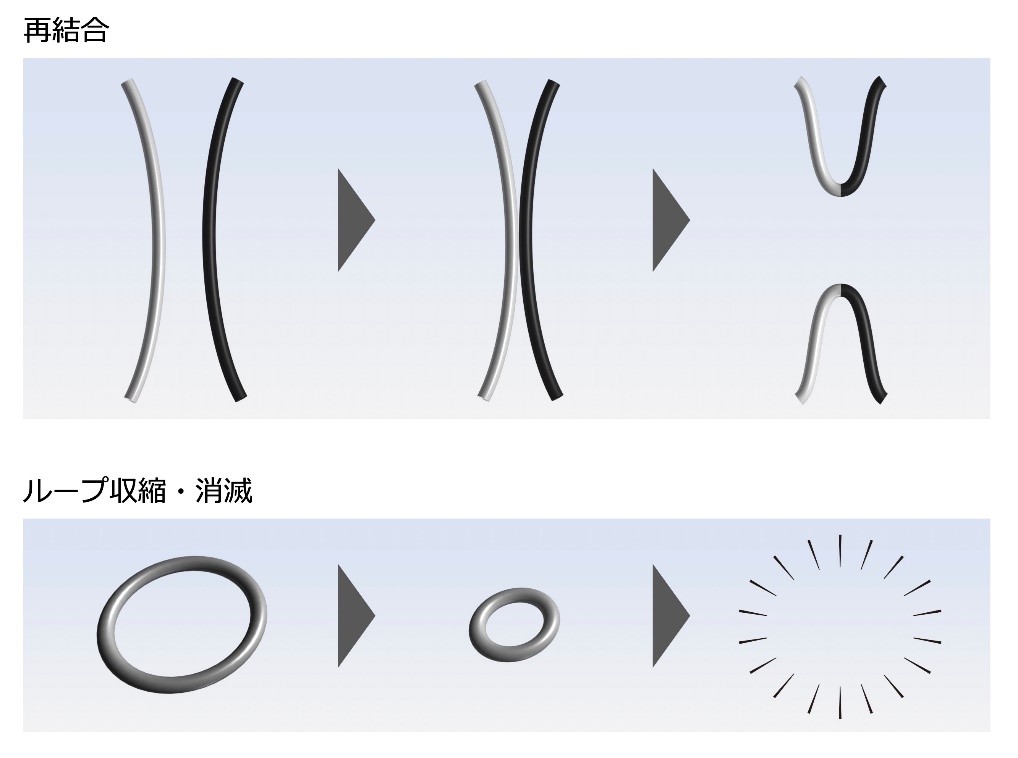
図3:線欠陥の再結合と、ループ収縮・消滅の模式図
発表内容
研究の背景
ネマチック液晶と呼ばれる典型的なタイプの液晶は、細長い分子で構成され、分子の向きを互いに揃える配向秩序を持つ。ところが、系全体で必ず分子の向きが揃うわけではなく、配向の整合しない特殊な領域が現れることがあり、これをトポロジカル欠陥と呼ぶ。2次元の場合のトポロジカル欠陥は図1右に示した構造をとる。トポロジカル欠陥の周りで、配向が1/2回転(180°回転)しており、回転方向に応じて+1/2欠陥、-1/2欠陥と呼ばれる。トポロジカル欠陥同士は、液晶弾性(注2)を通じて相互作用し運動する。3次元の場合には、ひも状のトポロジカル欠陥(線欠陥と呼ばれる)がよくみられる(図2左)。線欠陥の断面では、2次元欠陥の場合と同様に、配向が180°回転しているが、回転軸はどちらを向いていてもよい。線欠陥は変形を伴って運動し、ぶつかってつなぎ替わったり(再結合)、ループ状になってそのまま縮んで消えてしまったりする(図3)。
線欠陥の性質や運動は、それ自体への理学的な興味からも、光を曲げたりコロイド粒子をトラップしたりといった欠陥の持つ特性を応用する観点からも、盛んに研究され、液晶研究における一大トピックである。既存技術では、欠陥そのものではなく配向の3次元分布を観測する手法があり、原理的には配向から線欠陥の位置を特定可能だが、実際には欠陥周囲のイメージングには様々な困難が伴い、欠陥位置を3次元的に特定するのは容易ではない。そのため、これまでに数多く行われてきた線欠陥に関する研究は、特に運動については、2次元情報しか持たないものが中心であった。
研究内容
今回、静止した欠陥への蛍光色素の集積現象を運動観察に応用し、蛍光色素をトポロジカル欠陥のラベルとして利用することで、その3次元運動を共焦点顕微鏡(注3)で直接観測することに成功した。液晶に高電圧をかけて乱れた流れを起こすことで生成したトポロジカル欠陥が、電圧を切った後に動き回りながら次第に消えていく様子を観測した(動画1)。また今回の観測で、再結合やループ縮小・消滅といった線欠陥に特有の現象を捉えることに成功した(動画2, 3)。平行に近づくタイプの再結合に着目してより詳しい解析を行ったところ、2次元欠陥の運動と共通する性質と異なる性質の両方が明らかになった。まず3次元線欠陥が再結合の際どのように近づくか調べたところ、再結合時刻をとして、欠陥同士の距離は√(t0-t)に比例することが分かった。これは2次元の±1/2欠陥同士が近づきぶつかって消える対消滅の際に成り立つのと同様の法則であり、3次元線欠陥でも同じ法則が成り立っていた。さらに、再結合に向かって近づいてくる2本の線欠陥それぞれがどのように運動しているかも調べた。2次元欠陥の対消滅の場合には、流れ場の効果(注4)により、+1/2欠陥が-1/2欠陥よりも速く動くという非対称なふるまいが起きることが知られている。今回解析した線欠陥の運動は一見、2次元と同じように非対称であったが、解析を工夫し、注目している欠陥が周辺の領域から受ける影響を除くことで、実際には2次元の場合とは異なり対称に運動していることが明らかになった。このような2次元と3次元の対称性の違いは、次に説明する通り、トポロジーとエネルギーの観点から議論できる。まず、2次元で±1/2欠陥はトポロジーとして区別できるのに対し、3次元では区別できない。なぜなら、3次元では配向の回転軸がどの方向でも向けることから、+1/2欠陥と-1/2欠陥の中間的な構造も取ることができ、+1/2欠陥から-1/2欠陥へ連続的に変形できるので、±1/2欠陥とその中間構造は全てトポロジカルに等価となるためである(図4)。この中間構造の中には、近づく際に対称な運動をする構造(ねじれ欠陥、図2)があり、今回用いた液晶をはじめとしたほとんどの液晶で、この構造は他の構造よりエネルギーが低い(図4)。したがってトポロジーによって3次元でのみ許される構造が、エネルギー安定性のため、たしかに実現すると考察でき、実験的にも確認している。トポロジカル欠陥の概念は液晶に限られたものではないが、同様の議論は液晶以外のトポロジカル欠陥でも成り立つと考えられ、この「自発的対称性の回復」メカニズム(図4)には、液晶を超えた一般性があると期待される。
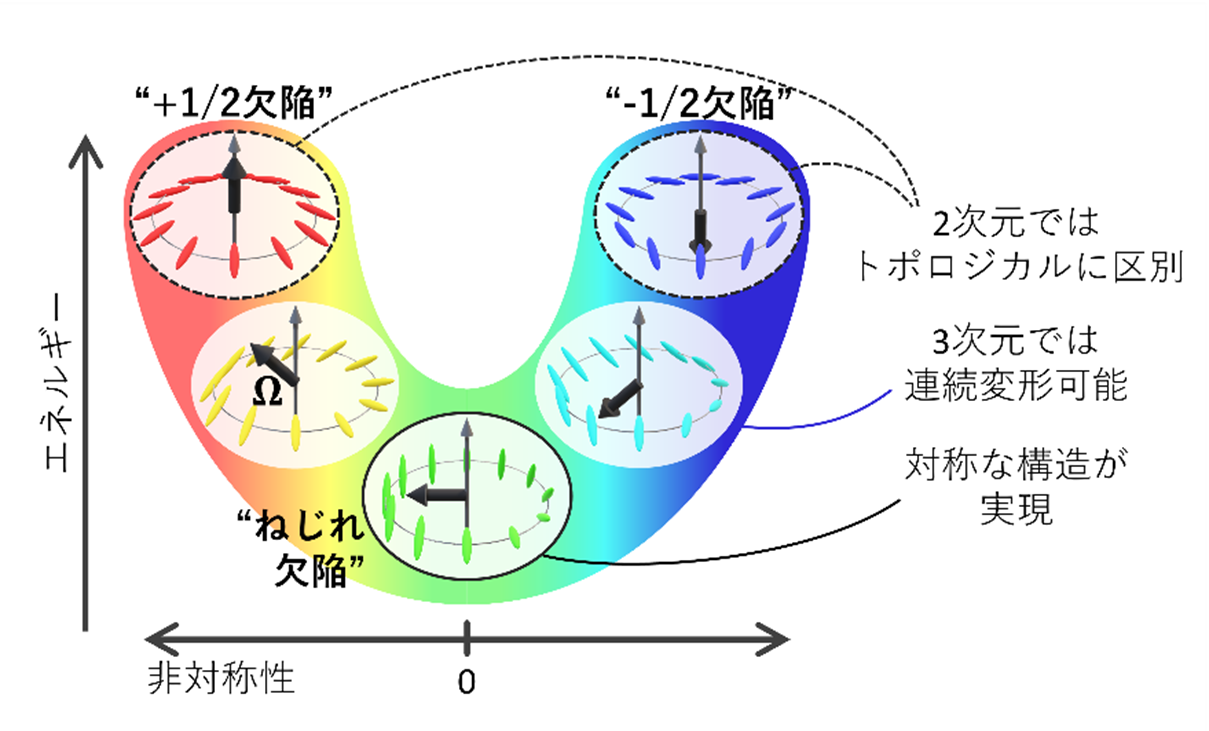
図4:2次元で見られなかった対称性が3次元では回復することを表す概念図
今後の展望
本研究で報告した液晶トポロジカル欠陥の3次元運動の可視化技術は、これまで2次元観測が中心であった欠陥研究にとって重要なツールとなると期待される。また、トポロジカル欠陥は、液晶だけにとどまらず、液体ヘリウム中の量子渦や宇宙論における宇宙ひもなど物理の広い領域に現れ重要な役割を果たしている。近年では生物系でも、細長い細胞や微生物などの集団的ふるまいが、液晶の理論やトポロジカル欠陥の概念で理解されるようになってきており、本研究で得られたトポロジカル欠陥の挙動に関する成果はトポロジカル欠陥がかかわる広い学問領域に貢献する可能性がある。
本研究は、科学技術振興機構(JST)さきがけ「トポロジカル材料科学と革新的機能創出(研究総括:村上 修一)」研究領域における「液晶トポロジカル乱流の構造決定と負粘性材料科学の開拓(課題番号JPMJPR18L6)」のほか、日本学術振興会による科研費(課題番号JP19H05800、JP19H05144、JP20H01826、JP22J12144)、東京大学におけるJSRフェローシップおよびFoPM WINGSプログラムの支援により実施されました。
発表雑誌
- 雑誌名
Proceedings of the National Academy of Sciences論文タイトル
Scaling and Spontaneous Symmetry Restoring of Topological Defect Dynamics in Liquid Crystal著者
Yohei Zushi and Kazumasa A. Takeuchi*DOI番号
10.1073/pnas.2207349119
用語解説
注1 トポロジー
連続的な変化(例えば図形なら曲げたり伸ばしたりといった連続的な変形)では変わらない性質を取り扱う数学の分野。よく出される例ではあるが、取手のついたマグカップの形は、カップ部分を縮め取手部分を膨らませることで、ドーナツ形に変化させることができる。切り貼りせず、曲げたり伸ばしたりするだけで、マグカップとドーナツは互いに行き来することができるので、トポロジーとして同一視される。この例では、「穴が一つ」という性質が共通しており、これをトポロジカル不変量という。同様に、トポロジカル欠陥とは、このような連続変形では変化(解消)しない欠陥という意味である。指紋の例では、皮膚を伸び縮みさせても、渦巻や枝分かれ、馬蹄状などの紋様は消えることはない。液晶の場合、+1/2欠陥と-1/2欠陥は、2次元では連続変形で互いに移し変えられずトポロジカルに区別される(±1/2はトポロジカル不変量であり、巻き数と呼ばれる)が、3次元では連続変形で移り変われるので、移り変わる途中の構造も含めてすべてトポロジカルに等価となる。
注2 液晶弾性
液晶配向の不均一性(揃わなさ)に由来する弾性。ひろがり、ねじれ、曲げの3つの変形モードに分類できる。液晶は流体であるので、通常の固体のような伸び縮みに関する弾性ではない。
注3 共焦点顕微鏡
ピンホールを用いてサンプルの1点から来た光だけを検出することで、通常の光学顕微鏡にはない奥行き方向の空間分解能を持つ顕微鏡。サンプル全体を走査することで、3次元情報を取得する。
注4 流れ場の効果
液晶には流動性があるため、分子の平均的な向きである配向の変化と、流体としての移動を関連付けて取り扱う必要がある。