2019-10-15 京都大学
石本健太 数理解析研究所准教授は、流体数値シミュレーションと数理解析によって、バクテリアの「くるくる回る」独楽(コマ)のような運動に潜む力学メカニズムを解明しました。
水回りのヌメリのようなバクテリア集団の形成は、1匹の細胞が壁面境界に付着することから始まります。しかし、バクテリアの壁面付近の振る舞いは複雑で、その解析は非常に困難です。近年、バクテリアが独楽のように回転する現象が注目されていますが、本研究では高精度の流体シミュレーションに加え、新たな流体理論を構築することで、バクテリア独楽が構造の柔らかさを巧みに利用していることが明らかになりました。
本研究成果は、細菌などの微生物の生存戦略の究明や、病原菌の付着を防止する技術開発につながることが期待されます。
本研究成果は、2019年10月10日に、国際学術誌「Journal of Fluid Mechanics」のオンライン版に掲載されました。

図:流体方程式から計算された流れの様子
詳しい研究内容について
微生物の運動に潜む柔らかな力学メカニズムを解明
―バクテリア「独楽」は如何にして廻るか―
概要
京都大学数理解析研究所石本健太 准教授は、流体数値シミュレーションと数理解析によって、バクテリア の’くるくる回る’独楽(コマ)のような運動に潜む力学メカニズムを解明しました。
水回りのヌメリのようなバクテリア集団の形成は、1匹の細胞が壁面境界に付着することから始まります。 しかし、バクテリアの壁面付近の振る舞いは複雑で、その解析は非常に困難です。近年、バクテリアが独楽の ように回転する現象が注目されていますが、本研究では高精度の流体シミュレーションに加え、新たな流体理 論を構築することで、バクテリア独楽が構造の柔らかさを巧みに利用していることが明らかになりました。こ の成果は、細菌などの微生物の生存戦略の究明や、病原菌の付着を防止する技術開発につながることが期待さ れます。
本成果は、2019 年 10 月 10 日に英国の国際学術誌「Journal of Fluid Mechanics」のオンライン版に掲載さ れました。
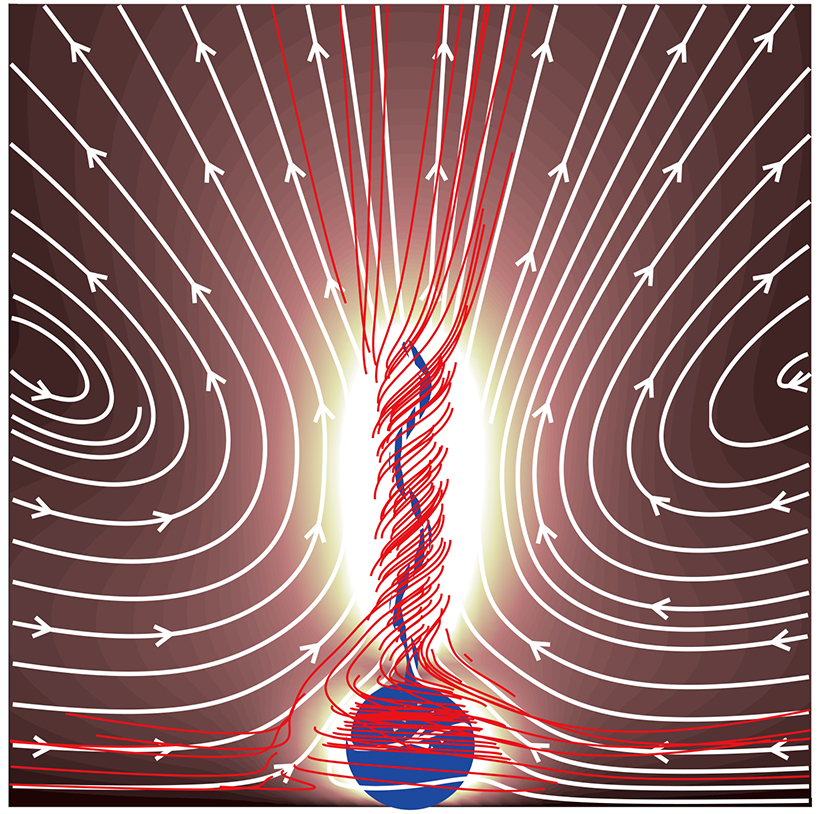 図:流体方程式から計算された流れの様子
図:流体方程式から計算された流れの様子
1.背景
台所や水回りのヌメリは細菌(バクテリア)のコロニー(集団)の最も身近な例ですが、これらの集団の形 成は、1匹の細胞が壁面に付着することから始まります。バクテリアの表面には鞭毛(べんもう)と呼ばれる、 らせん形状のスクリューのような突起物が生えており、この鞭毛を表面の付け根部分にある分子モーターで回 転させることにより、液体中を泳ぐことができます。このように泳いできたバクテリアの壁面付近での振る舞 いは、バクテリア集団形成のメカニズムを理解する上での基礎であり、非常に重要な問題です。
バクテリアの形態は非常に多様で、壁面表面での運動も多岐にわたります。壁面にそって円を描くように泳 ぐ種類や、おもちゃの独楽(コマ)のようにある場所でくるくると回り続ける種類もいます。これらの運動の メカニズムを理解するためには、鞭毛の回転によって生まれる液体の流れ、そして推進力を受けて自転しなが ら推進するバクテリアの運動、壁面境界付近での摩擦力の効果、を考慮する必要がありますが、これらはお互 いに影響しあっているため、問題は非常に複雑になっています。そのため、どのようなバクテリアが表面付近 でどのような振る舞いをするのか、統一的で一般的な理論解析が行われていませんでした。
一方、おもちゃの独楽の運動は一見簡単そうでいてその挙動を解析することは難しく、独楽の運動を記述す る方程式は 19 世紀の末にはフランス科学アカデミーの数学コンクールの懸賞問題にもなり、その後の数学の 発展にも大きな影響を与えました。ミクロの世界のバクテリアの独楽のような運動は、おもちゃの独楽の運動 とはそのメカニズムは異なり、周りの液体の粘性の効果が強くなるため、液体の運動を表す流体力学の数式を 解析する必要があります。このように、微生物学の基礎問題として重要な現象であるということだけでなく、 運動を記述する方程式そのものへの数理的な強い興味・関心もあり、バクテリアの独楽の運動を理論的に解析 する研究に取り組むことにしました。
2.研究手法・成果
壁面境界付近のバクテリアの振る舞いを調べるためには、流体の方程式をコンピュータを用いて高精度で解 くことが必要になります。バクテリアの鞭毛の付け根部分はフックと呼ばれる非常に柔らかな部位で接続され ています。本研究では、フックの柔らかさも考慮した流体数値シミュレーションで運動を解析しました。その 結果、独楽の運動をはじめ、実際の実験結果と同様の様々な運動パターンを再現することに成功しました。
数値シミュレーションでは、具体的な形状や条件を入力数値として設定する必要があることから、大規模な シミュレーションになるほど解析に時間がかかり、また扱うデータの大きさも大きくなってくるため、一般的 で包括的な仕組みを調べることが難しくなります。そのため、メカニズムの理解を進めるためには流体の方程 式を一般的に解いていくような理論解析が非常に有効です。しかし、今までは、複雑な物体の形状と流れの効 果のために、微生物の遊泳運動の解析理論は個別の微生物や数理モデルにのみ適用可能なものに限られてきま した。本研究では、物体形状の幾何学的な対称性に注目することで、生物の遊泳運動を記述するための一般的 で包括的な流体理論を構築することに成功しました。
この理論を用いて独楽の運動の安定性を解析したところ、数値シミュレーションの結果をよく再現すること ができました。また、鞭毛スクリューが回転することにより、流れを押し出す力と本体を回転させる力が生ま れます。理論の解析によって、押す力はバクテリアの鞭毛の長さによって効果が異なるものの、主に独楽の自 立を不安定にさせ、傾ける効果があることが分かりました。一方で回転させる力は、フックの柔らかさに応じ て効果が異なるものの、程よい柔らかさの場合には、独楽の自立を助け、その位置を安定化させる効果がある ことがわかりました。この両者の力のバランスにより運動の安定性が決まっていますが、フックの柔軟性が無 ければ、独楽の運動は通常、常に不安定で、自立することはできません。おもちゃの独楽とは異なり、バクテ リアの独楽の運動は、起き上がりこぼしのように、自発的に自らの力で起き上がっており、フックの柔らかさ を巧みに利用した現象だと言えます。
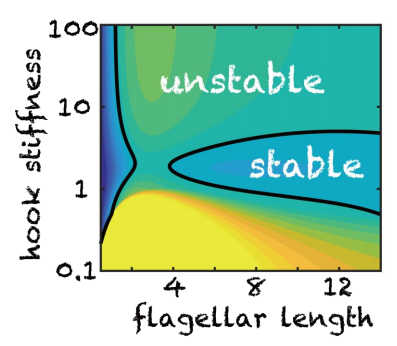
図:バクテリア独楽の安定性理論解析の結果。鞭毛の長さ(flagellar length)が十分長く、程よいフックのかたさ(hook stiffness)をもつ場合に限って、独楽のような自立運動が安定になることを示している。
3.波及効果、今後の予定
本研究は、微生物の運動に潜む、物体の構造自身のもつ柔軟性と、微生物周辺の流体の、複雑な力学的な 相互作用を理論的に解析したことに大きな意義があります。境界付近のバクテリアのダイナミクスの包括的 な深い理解は、バクテリアコロニーの形成メカニズム解明への貢献が期待され、これは、バクテリアを含む 微生物の生態や進化の理解だけでなく、感染症の予防技術に役立つと考えられます。また、構造の柔らかさ は、運動に大きな自由度を生み出すことができるので、入力信号に対して多様な運動様式を実現することが 容易です。このように、生き物の仕組みを学ぶことで、柔らかさを巧みに用いたマイクロロボット開発の基 礎を担うと考えられます。本研究で構築した流体理論は、さらなる一般化や拡張の余地を残しており、理論 の展開が期待されます。
4.研究プロジェクトについて
本研究は科学研究費補助金(若手研究・18K13456)、及び文部科学省卓越研究員事業の支援を受けまし た。流体数値シミュレーションには京都大学数理解析研究所、及び京都大学情報環境機構のスーパーコンピ ュータシステムを利用しました。また、本研究は日本学術振興会海外特別研究員として英国オックスフォー ド大学滞在時に実施したものです。
<研究者のコメント>
微生物の運動は、複雑さの中にも数理的に記述可能な仕組みがあり、流れを介した生き物の形と運動の関係 には、まだまだ隠された普遍的な法則・数理的構造が存在しているように感じています。
<論文タイトルと著者>
タイトル:Bacterial spinning top(バクテリア独楽)
著 者:Kenta Ishimoto
掲 載 誌:Journal of Fluid Mechanics DOI:10.1017/jfm.2019.714
リンク — 「数理の目で見る精子の旅」 http://www.kyoto-u.ac.jp/ja/research/research_results/2016/170324_2.html
<イメージ図>