繊維製造やロボット美容師への応用が期待される「ほぐし」を数学的に理解する研究成果を発表 Researchers develop a mathematical understanding of detangling that could be used for textile manufacturing, robotic hairdressers
2022-04-13 ハーバード大学
・Mahadevan氏と共著者のThomas Plumb Reyes氏、Nicholas Charles氏は、Soft Matter誌に掲載された新しい論文で、櫛でとかすことの数学について調べ、なぜ多くの人が使うブラッシング技術が繊維の束をほぐす最も有効な方法であるのかを説明しています。
・髪をとかすには、相互作用する弾性フィラメントの束として定義される、集合的なカールのトポロジーのもつれを払いのけることが含まれます。実験と計算を組み合わせて、トポロジー、幾何学、力学を自然に結びつけるこの問題を研究しました。
<関連情報>
- https://www.seas.harvard.edu/news/2022/04/tear-free-brushing-all-you-need-math
- https://pubs.rsc.org/en/Content/ArticleLanding/2022/SM/D1SM01533H
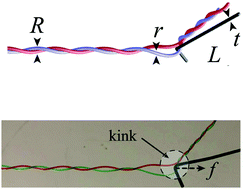
二重らせんを解く Combing a double helix
Thomas B. Plumb-Reyes, Nicholas Charles and L. Mahadevan
Soft Matter First published:22 Mar 2022
DOIhttps://doi.org/10.1039/D1SM01533H
Abstract
Combing hair involves brushing away the topological tangles in a collective curl, defined as a bundle of interacting elastic filaments. Using a combination of experiment and computation, we study this problem that naturally links topology, geometry and mechanics. Observations show that the dominant interactions in hair are those of a two-body nature, corresponding to a braided homochiral double helix. This minimal model allows us to study the detangling of an elastic double helix driven by a single stiff tine that moves along it and leaves two untangled filaments in its wake. Our results quantify how the mechanics of detangling correlates with the dynamics of a topological quantity, the link density, that propagates ahead of the tine and flows out the free end as a link current. This in turn provides a measure of the maximum characteristic length of a single combing stroke in the many-body problem on a head of hair, producing an optimal combing strategy that balances trade-offs between comfort, efficiency and speed of combing in hair curls of varying geometrical and topological complexity.