UHのエンジニアが、行動予測と天気予報の改善を可能にする方法を開発 UH Engineer Develops Method That Can Predict Behavior, Improve Weather Forecasting
2022-12-08 ヒューストン大学(UH)
コンパクトでありながら正確なモデルの構築を始めるには、1つの原則が基本となる。一見複雑でランダムに見える行動にも、その根底にはシステムをコンパクトに表現するためのパターンが存在するのだ。
機械学習と多様体の数理理論から得たアイデアを用いることで、この手法はシミュレーションを非常に高速かつ安価に行うことができる。
研究者は、あるアプリケーションで、2種類の化学物質間の反応をシミュレーションした。この反応では、化学物質同士が出会ったときに複雑な挙動を示す。つまり、リズミカルな螺旋状の反応を繰り返し、そのシミュレーションには2万以上の変数が必要だった。研究者は、反応のビデオをアルゴリズムに送り込み、その反応を理解するためにたった1つの変数が必要であることを発見した。それは、時計の秒針のように、螺旋が元の位置に戻ってくる時間である。
天気予報の場合、数値モデルとは、複雑な物理学や流体力学の方程式を使って大気をコンピューターでシミュレーションすることである。
<関連情報>
- https://uh.edu/news-events/stories/2022-news-articles/december-2022/12082022-floryan-data-variables-simulations-speed.php
- https://www.nature.com/articles/s42256-022-00575-4
データ駆動型固有ダイナミクスの発見 Data-driven discovery of intrinsic dynamics
Daniel Floryan & Michael D. Graham
Nature Machine Intelligence Published:08 December 2022
DOI:https://doi.org/10.1038/s42256-022-00575-4
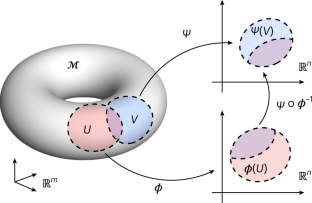
Abstract
Dynamical models underpin our ability to understand and predict the behaviour of natural systems. Whether dynamical models are developed from first-principles derivations or from observational data, they are predicated on our choice of state variables. The choice of state variables is driven by convenience and intuition, and, in data-driven cases, the observed variables are often chosen to be the state variables. The dimensionality of these variables (and consequently the dynamical models) can be arbitrarily large, obscuring the underlying behaviour of the system. In truth these variables are often highly redundant and the system is driven by a much smaller set of latent intrinsic variables. In this study we combine the mathematical theory of manifolds with the representational capacity of neural networks to develop a method that learns a system’s intrinsic state variables directly from time-series data, as well as predictive models for their dynamics. What distinguishes our method is its ability to reduce data to the intrinsic dimensionality of the nonlinear manifold they live on. This ability is enabled by the concepts of charts and atlases from the theory of manifolds, whereby a manifold is represented by a collection of patches that are sewn together—a necessary representation to attain intrinsic dimensionality. We demonstrate this approach on several high-dimensional systems with low-dimensional behaviour. The resulting framework provides the ability to develop dynamical models of the lowest possible dimension, capturing the essence of a system.



