2022-04-26 理化学研究所,慶應義塾大学,科学技術振興機構
理化学研究所(理研)革新知能統合研究センター数理科学チームの桑原知剛研究員(研究当時、現開拓研究本部桑原量子複雑性解析理研白眉研究チーム理研白眉研究チームリーダー、量子コンピュータ研究センター量子複雑性解析理研白眉研究チーム理研白眉研究チームリーダー)と慶應義塾大学理工学部の齊藤圭司教授の共同研究チームは、量子力学に従う多粒子系(量子多体系[1])の熱平衡状態[2]では、一般に長距離に及ぶ「量子もつれ[3]」が存在しないことを示しました。
本研究成果は、量子機械学習[4]を含む量子計算に関する手掛かりを多く与えるとともに、有限温度[5]で観測されるさまざまな量子的物理現象に関与する量子もつれの分類研究に寄与すると期待できます。
量子コンピュータ[6]を使った量子計算には、量子もつれが本質的な役割を果たすため、量子もつれの有限温度における効果を解き明かすことは重要な未解決問題の一つでした。
今回、共同研究チームは二つの領域で定義される標準的な2者間の量子もつれの量を解析的に評価し、十分離れている二つの領域間に生じる量子もつれは有限温度において劇的に小さくなることを突き止めました。この結果は、一般的な量子多体系において、2者間の量子もつれは絶対零度(約-273℃)では存在し得ますが、有限温度では、特殊な3者間量子もつれ以外は生き残ることができないことを示しています。
本研究は、オンライン科学雑誌『Physical Review X』(4月27日付)に掲載されます。
背景
古典力学(ニュートン力学で表される)に従う粒子と量子力学に従う粒子とでは、多くの点で異なる性質があります。古典力学に従う粒子では、初期時刻で位置と運動量が定まれば、任意の時刻での位置と運動量が確定しますが、量子力学に従う粒子は粒子性と波動性という2面性を持ち、粒子の位置や運動量の実験的な測定値は確率的になります。また、古典力学に従う多粒子の運動では、一般的に相転移[7]などの特別な現象が起きない限り、多数の粒子を通して遠く離れた粒子同士が影響を及ぼし合うことはありません。ところが、量子力学の世界では、一般的に古典力学の世界では生じ得ない非自明な相関が生じ得ます。
例えば、二つの電子のスピン[8]を量子力学的に特殊な状態にした後、それぞれの電子を遠く離れた領域Aと領域Bに置きます。その際、領域AB間に他の粒子が存在していても構いません。古典力学の世界では、一般に離れた粒子は独立した粒子として振る舞いますが、量子力学的な特殊な状態では、どんなにAB間の距離が離れていても、一方のスピンが上向き(下向き)なら、もう一方のスピンは必ず下向き(上向き)になる、といった奇妙な相関を作ることができます。このような相関を「量子もつれ」と呼びます。
量子もつれを特徴付ける方法として、量子力学に従う多粒子系(量子多体系)における領域Aと領域Bにある原子のみを考える、「2者間量子もつれ」が標準的な量子もつれの指標として知られています(図1左)。一方で、多種多様な量子計算を実現するためには、2者間よりも多くの粒子間で量子もつれを作る必要が出てきます。例えば、「3者間量子もつれ」の代表的な例として、領域Aと領域Bの量子もつれを領域Cの状態に応じて定義する「トポロジカルエンタングルメントエントロピー[9]」などが非自明な量子もつれとして注目されています(図1右)。
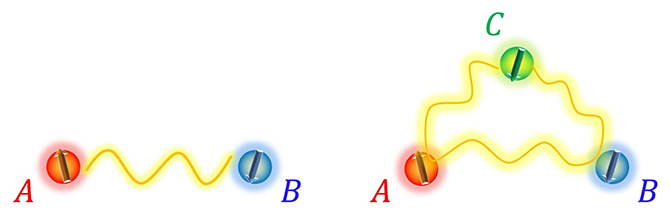
図1 2者間量子もつれ(左)と3者間量子もつれ(右)の概念図
左は、量子多体系において、領域Aと領域Bにある原子だけを考える標準的な量子もつれの指標。
右は、領域Aと領域Bの量子もつれを、領域Cの状態に応じて定義する。
量子コンピュータを使った計算(量子計算)には、量子もつれが重要な原理の一つであることが知られています。量子コンピュータは量子多体系と見なすことができることから、一般の量子多体系において量子もつれを分類し、どのような量子もつれが安定に存在できるのかを明らかにすることは、基礎科学的にも応用的にも重要なテーマです。
一般的に量子多体系は、有限温度の熱浴(一定の温度を保っている十分大きな外界)に接触して有限温度の状態になります。このとき、量子もつれにはどのような一般的性質があるのかという問題は未解決のままです。この問題を解決することは、量子コンピュータが有限温度で動作するために必要な量子もつれを特定する際の手助けになるほか、さまざまな固体で生じる有限温度での非自明な量子現象において、量子もつれの役割を理解する上でも大きな手掛かりを与えるはずです。有限温度の状態は、一般に「熱平衡状態」であり、個々のエネルギー固有状態が指数分布に従って確率的に混ざった状態で表されます。
そこで、共同研究チームは、一般の量子多体系の熱平衡状態には、量子もつれといえる状態がどの程度隠されているかという課題に取り組みました。
研究手法と成果
共同研究チームは、図2(a)で示される量子多体系における標準的な2者間量子もつれに注目し、その有限温度における普遍的な性質を明らかにすることを目指しました。
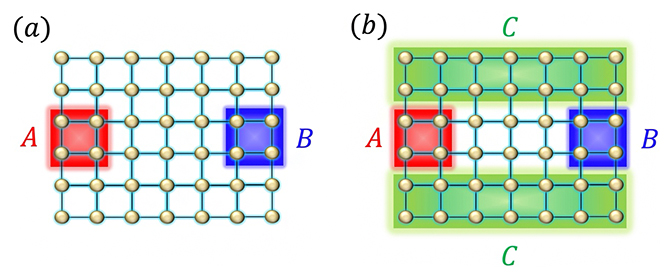
図2 量子多体系での熱平衡状態の量子もつれの概念図
(a)領域Aと領域Bのみを考える2者間量子もつれであり、標準的な量子もつれの指標。
(b)領域Cの状態に応じて決まる領域Aと領域B間の3者間量子もつれ(トポロジカルエンタングルメントエントロピー)。特殊な量子もつれを特徴付ける一例である。
本研究では、標準的な量子もつれ(a)に着目し、有限温度での普遍的な性質を明らかにした。
量子もつれの構造は、量子多体系で理論的に解析することが極めて困難であることが知られています。そのため従来の研究では、特殊な場合に限定したり、数値計算手法を用いた方法で解析したりすることがほとんどでした。
量子もつれの普遍的な法則を解明するために、まず「量子相関」と呼ばれる新しい量を定義しました。物理学のさまざまな研究では、領域Aと領域Bにおけるそれぞれの観測量に対して熱平衡状態での相関関数が議論されます。この伝統的な相関関数を本課題のために拡張しました。この量子相関は、量子もつれがない状態と量子もつれがある状態を区別できると期待される量です。その上で領域Aと領域Bが十分に離れている場合、量子相関の大きさはAB間の距離に対して指数関数的に小さくなる(AB間の距離が大きいほど指数関数的に小さくなる)ことを数学的に証明しました。
さらに、この量子相関がAB間の距離に対して指数関数的に減衰することを用いて、相対エンタングルメントエントロピー[10]という量子もつれの指標に関して普遍的な性質を解明しました。領域Aと領域Bが十分に離れているとき、熱平衡分布が、量子もつれを示さない分布とどれくらい近い分布になっているかを解析しました。その結果、やはり有限温度では、領域Aと領域Bが十分に離れている場合、量子もつれの大きさはAB間の距離に対して指数関数的に小さくなることを証明できました。
これらは、標準的な量子もつれは絶対零度(約-273℃、あるいはその付近の極低温)においてのみ存在し、有限温度では生き残れないという重要な結果を示しています。また同時に、ここで扱った2者間の量子もつれでは表現できない特殊な量子もつれのみが有限温度で生き残れることも意味しています。例えば、図2(b)で示したトポロジカルエンタングルメントエントロピーは、3者間の特殊な量子もつれの一例ですが、有限温度でも生き残る可能性が知られています。
つまり、一般的な量子多体系において、2者間の量子もつれは絶対零度では存在し得ますが、有限温度においては、特殊な3者間量子もつれ以外は生き残ることができないということです。言い換えると、固体が示す有限温度の量子効果において、特殊な量子もつれのみが存在するはずであることを示唆しています。
今後の期待
本研究を通して、有限温度における量子もつれの普遍法則の一つが解明されました。どのような特殊な量子もつれが有限温度で生き残れるのかに関しては、今後の重要な課題になります。本成果は今後、量子機械学習を含む量子計算や物質が示す特異な量子現象の理解につながると期待できます。
補足説明
1.量子多体系
量子力学に従って互いに相互作用する多粒子系。
2.熱平衡状態
一定の温度の熱浴に接触し、見かけ上熱交換が生じていない状態。
3.量子もつれ
異なる粒子間に現れる量子力学特有の相関。
4.量子機械学習
量子コンピュータを用いて機械学習の問題を効率的に解くこと。一部の問題は量子コンピュータによって超高速化が達成できることが知られている。
5.有限温度
絶対零度(0ケルビン、約-273℃)でも無限大でもない一定の温度のこと。
6.量子コンピュータ
量子力学の原理を用いて、高速に動作する計算機。
7.相転移
水が氷になったり、水蒸気になったりというように、物質のマクロな状態が変化すること。
8.スピン
回転の自由度に似た、量子力学特有の状態。
9.トポロジカルエンタングルメントエントロピー
注目する領域以外の状態も反映させた量子もつれであり、さまざまな量子現象に現れることが知られてきている。
10.相対エンタングルメントエントロピー
量子もつれの大きさを測る最も基本的な指標の一つ。ある量子状態に対して、量子もつれを持たない状態との距離を情報論的に定量化したものに対応している。
研究支援
本研究は、日本学術振興会(JSPS)科学研究費補助金若手研究「テンソルネットワーク形式を用いた量子多体問題の計算複雑性解析(研究代表者:桑原知剛)」、科学技術振興機構(JST)戦略的創造研究推進事業(さきがけ) 「量子多体理論を用いた量子計算機の高速アルゴリズムの開発(研究代表者:桑原知剛、JPMJPR2116)」による支援を受けて行われました。
原論文情報
Tomotaka Kuwahara and Keiji Saito, “Exponential clustering of bipartite quantum entanglement at arbitrary temperatures”, Physical Review X
発表者
理化学研究所
革新知能統合研究センター 数理科学チーム
研究員(研究当時) 桑原 知剛(くわはら ともたか)
(現 開拓研究本部 桑原量子複雑性解析理研白眉研究チーム 理研白眉研究チームリーダー、量子コンピュータ研究センター 量子複雑性解析理研白眉研究チーム 理研白眉研究チームリーダー)
慶應義塾大学
理工学部
教授 齊藤 圭司(さいとう けいじ)
報道担当
理化学研究所 広報室 報道担当
慶應義塾 広報室
科学技術振興機構 広報課
JST事業に関する窓口
科学技術振興機構 戦略研究推進部 グリーンイノベーショングループ
嶋林 ゆう子(しまばやし ゆうこ)