2021-12-09 理化学研究所
理化学研究所(理研)数理創造プログラムの大下翔誉基礎科学特別研究員は、ブラックホール[1]の振動パターンのうち、最も励起されやすい振動パターンの「普遍的な組み合わせ」を理論計算から明らかにしました。
本研究成果は、ブラックホール連星[1]の合体直後に伝搬する時空のひずみ(重力波[2])の観測データによるブラックホールの重さや回転速度の測定や、アインシュタインの一般相対性理論[3]の精密な検証に貢献すると期待できます。
今回、大下基礎科学特別研究員は、ブラックホールが潜在的に持つ特徴的な振動パターンのうち、最も減衰率の低い21の振動パターンに対して、それらの「励起のしやすさ(振動のしやすさ)」を表す励起因子[4]を世界で初めて解析的に評価しました。その結果、ブラックホール連星が合体して形成されるブラックホールでは、5、6、7番目に減衰率の低い三つの振動パターンが最も励起されやすいことを示しました。理論的に予言されたそれらの振動の重ね合わせは、ブラックホール連星合体直後に放射される重力波のシミュレーション波形の解析結果を適切に説明することを示しました。本研究成果により、ブラックホールの揺らぎから放射される重力波を高い精度でモデル化し、重力の標準的理論とされる一般相対性理論を、高い精度で検証できる可能性があります。
本研究は、科学雑誌『Physical Review D』オンライン版(12月9日付)に掲載される予定です。

ブラックホールの揺らぎのイメージ図(絵: 大下翔誉)
背景
アインシュタインが時空の物理を記述する理論として一般相対性理論を提唱してから100年後の2015年、米国のレーザー干渉計重力波観測装置(LIGO)[5]がブラックホールの合体により放射された重力波を初めて検出しました。以来、数多くのブラックホール合体現象で放射された重力波が検出されています。
孤立するブラックホール連星は互いに徐々に近づき、最終的に合体して、一つの大きなブラックホールを形成します。そして、合体直後に放射される重力波から、形成されたブラックホールの「揺らぎ」を見ることができます(図1)。一般相対性理論によれば、ブラックホールの重さと回転速度だけで決まるブラックホールの準固有振動[6]の重ね合わせで、合体後に放射される重力波の波形を記述できます。つまり、観測された重力波の波形から合体後のブラックホールの固有振動を読み取ることで、連星合体後のブラックホールの重さや回転速度を測定し、一般相対性理論の検証につなげることができます。
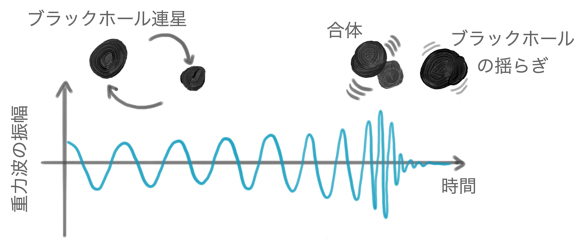
図1 ブラックホール連星合体と放射される重力波の概念図
ブラックホール連星は、互いの重心周りを周回運動しながら重力波を放射する。次第にその重力波放射でエネルギーを失い、二つのブラックホールは互いの重力で引き寄せられて合体する。合体直後のブラックホールは、重力波放射を伴う減衰振動をしながら、最終的に一つの静的なブラックホールになる。
ブラックホールの振動は強い減衰を伴うため、重力波の波形からその固有振動を精密に読み取ることは困難だと考えられています。一方で、米国の研究グループ注1)は、数値シミュレーション注2)のデータ解析を行い、ブラックホール合体時に、減衰の強い振動が大きな振幅で励起される間接的な証拠を報告しています。これが事実であれば、ブラックホールの準固有振動を高い精度で測定できます。そのため、なぜ、そしてどのような場合に、減衰率の高い振動パターンが強く励起されるのかを理論に基づいて系統的に理解し、裏付けをすることが、重要課題の一つでした。
注1)M. Giesler et al. “Black hole ringdown: the importance of overtones”, Phys. Rev. X 9, 041060 (2019).
注2)M. Boyle et al. “The SXS Collaboration catalog of binary black hole simulations”, Class. Quantum Grav. 36, 195006 (2019).
研究手法と成果
理論上、ブラックホールの振動パターンは無数に存在し、それぞれのパターンは振動数と減衰率によって特徴付けられます。さらに、それぞれの振動パターンは「励起のしやすさ(振動のしやすさ)」が決まっており、それは「励起因子」と呼ばれる値で評価できます。これまでは、最も減衰率が低い四つの振動パターンに対してだけ、励起因子が精密に計算されていました注3)。
今回、大下基礎科学特別研究員は、まず、計算上扱いやすいホイン関数[7]によって膨張宇宙におけるブラックホールの揺らぎを厳密に記述できることを用いて、膨張宇宙内のブラックホールが固有に持つ21の振動パターンに対して、励起因子を計算しました。さらに、実際の宇宙では宇宙膨張の効果は極めて小さいため、空間膨張が弱い極限での励起因子を評価する方法を開発しました。その結果、ブラックホールの回転パラメータ[8]を典型的な値である0.7にした場合、5、6、7番目に減衰率の低い振動パターンがブラックホール合体時に最も強く励起されやすいことを理論計算から示しました(図2)。
注3)Z. Zhang, E. Berti, and V. Cardoso, “Quasinormal ringing of Kerr black holes. II. Excitation by particles falling radially with arbitrary energy”, Phys. Rev. D 88, 044018 (2013).
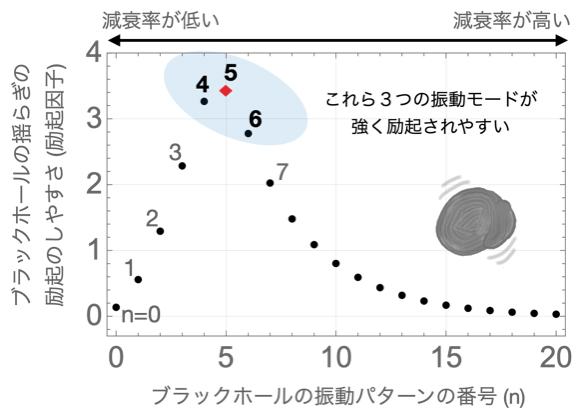
図2 ブラックホールのそれぞれの固有振動に対する励起因子の値
ブラックホールの回転パラメータを典型的な値である0.7にした場合、連星合体後の典型的なブラックホールにおいて、励起されやすい振動はn=4, 5, 6(5、6、7番目に減衰率の低い振動)である。その中でも赤点で示したn=5(6番目に減衰率の低い振動)が最も励起されやすい。
ブラックホール合体後に放射される重力波の振幅は、今回計算されたブラックホールの重さと回転速度だけで決まる励起因子の値と、ブラックホール合体の詳細(どのような衝撃が与えられたか)などで決まる「ソース因子」の値のかけ算で決まります。先行研究で行われたシミュレーションの解析結果と励起因子の値を用いてソース因子を評価したところ、合体後の重力波波形は、ソース因子よりも励起因子の振る舞いで主に決まることが分かりました(図3)。これは、今回得られた5、6、7番目に減衰率の低い振動パターンの「普遍的な組み合わせ」が、ブラックホール連星合体後の主要な振動を記述することを示しています。
今回理論的に得られたブラックホールの振動の組み合わせは、実際の観測データや数値シミュレーションの解析とは独立に導かれたものであり、これまでデータ解析だけで見いだされていたブラックホールの揺らぎの特徴を、世界で初めて理論的に説明することに成功しました。

図3 ブラックホールの固有振動それぞれに対する励起因子とソース因子の相対値
ソース因子はブラックホールの揺らぎの初期条件で決まる。ソース因子の相対値はほぼ1であるのに対し、励起因子の相対値は大きいことから、ブラックホールの主要な振動パターンの組み合わせは、主に励起因子の振る舞いで決定されることが分かる。(※ソース因子の評価には、米国の研究グループ注1)による数値シミュレーション注2)の解析結果を併用)
今後の期待
本研究成果は、ブラックホールの合体の詳細によらず、揺らぎのパターンの組み合わせがほぼ励起因子の値で決まることを示唆しており、ブラックホールの揺らぎから放射される重力波の波形の理論的モデル化に貢献すると期待できます。
さらに、今後の重力波観測で探るブラックホールの揺らぎの物理的な理解、そして一般相対性理論から導かれる「ブラックホールの無毛定理[9]」のさらなる精密検証にも応用できる可能性があります。
補足説明
1.ブラックホール、ブラックホール連星
ブラックホールは、重さを持つ物体が自重を圧力などで支えきれず、極限までつぶれることで形成される天体。ブラックホール連星は、二つのブラックホールが互いに重力で束縛し合いながら、両者の重心の周りを周回運動する天体。
2.重力波
質量を持った物体が運動するときに発生し、周囲に伝播する時空のゆがみ(曲率)。一般相対性理論では、重力波の伝播速度は光の速度と同じである。
3.一般相対性理論
アインシュタインが確立した時空の運動を記述する理論。この理論を基に、ブラックホールの存在や、宇宙の膨張、重力波などが予言された。
4.励起因子
ブラックホールが持つ準固有振動の「振動しやすさ」を表す物理量。この値は、ブラックホールの重さと回転速度だけで決まる普遍的な量であり、ブラックホールをどのように揺らがせたか、という詳細には一切依存しない。
5.レーザー干渉計重力波観測装置(LIGO)
米国ルイジアナ州リビングストンとワシントン州ハンフォードの二つに位置するレーザー干渉計であり、地上に到達した重力波を観測するべく設立された。2015年9月14日(協定世界時)に、ブラックホール連星合体から放射される重力波を世界で初めて観測した。その功績により、重力波観測の先駆者であるバリー・バリッシュ博士、キップ・ソーン博士、レイナー・ワイス博士に2017年ノーベル物理学賞が授与された。
6.ブラックホールの準固有振動
ブラックホールが固有に持つ振動パターンであり、無数に存在する。それぞれの振動パターンは、離散的な振動数と減衰率で特徴付けられる。ブラックホールだけでなく、地上のあらゆる物体にも固有の振動パターンがある。楽器がある決まった音を出すのも、ブランコをうまく揺らすために決まった周期で屈伸運動をする必要があるのも、これが理由である。
7.ホイン関数
その性質が数学的によく理解されている特殊関数の一種。膨張宇宙に存在するブラックホールの揺らぎの方程式がホイン微分方程式で記述されることは、日本人物理学者の鈴木久男博士、高杉英一博士、梅津裕志博士らによって示された注4)。
注4)H. Suzuki, E. Takasugi, and H. Umetsu, “Perturbations of Kerr-de Sitter black hole and Heun’s equations”, Prog. Theor. Phys. 100 (1998) 491-505.
8.ブラックホールの回転パラメータ
ブラックホールの回転パラメータは、ブラックホールの自転の強さを表す角運動量と重さの2乗の比で与えられる。重力の強さを表す万有引力定数や光速を1とする単位系で、回転パラメータの値が1未満の範囲において、ブラックホールの自転が許される。回転パラメータが1を超えるほど激しい自転を伴うブラックホールでは、重力よりも遠心力が勝り、万物を吸い込むようなブラックホール特有の時空構造は失われる。このとき現れる時空構造は「裸の特異点」と呼ばれ、もはやそれはブラックホールに該当しない。
9.ブラックホールの無毛定理
一般相対性理論から得られる「ブラックホールは、重さと回転と電荷だけで特徴付けられること」を示す定理。もし、これ以外に孤立するブラックホールを特徴付ける量があると分かれば、一般相対性理論の修正が求められることになる。
研究支援
本研究は、理化学研究所2021年度独創的研究提案制度・奨励課題「Study of the ease-of-excitation of black hole perturbations: Towards the establishment of a revolutionary method to test gravity theories based on the observation of gravitational waves from blackholes(研究代表者:大下翔誉)」、日本学術振興会科学研究費助成事業研究活動スタート支援「宇宙論および素粒子論への応用に向けた真空相転移の基礎研究(研究代表者:大下翔誉)」(21K20371)、および理化学研究所基礎科学特別研究員制度の研究費による支援を受けて行われました。
原論文情報
Naritaka Oshita, “Ease of excitation of black hole ringing: Quantifying the importance of overtones by the excitation factors”, Physical Review D, 10.1103/PhysRevD.104.124007
発表者
理化学研究所
数理創造プログラム
基礎科学特別研究員 大下 翔誉(おおした なりたか)
報道担当
理化学研究所 広報室 報道担当



