ゴム製品の強靭化・薄型化による省資源化・軽量化への第一歩
2021-07-30 東京大学
○発表者:
梅野 宜崇(東京大学 生産技術研究所 教授)
久保 淳 (東京大学 生産技術研究所 助教)
作道 直幸(東京大学 大学院工学系研究科 バイオエンジニアリング専攻 特任助教)
奥村 剛 (お茶の水女子大学 基幹研究院 教授)
森下 善広(株式会社ブリヂストン 先端材料部門 研究員)
角田 克彦(株式会社ブリヂストン 先端材料部門 首席研究主幹)
浦山 健治(京都工芸繊維大学 材料化学系 教授)
○発表のポイント:
◆ゴム材料に加える外力が一定値を超えると、亀裂が広がる速度が急激に上がることが知られている。この現象が、亀裂先端でゴムからガラスへと状態が変わることによって生じることを明らかにした。
◆数値シミュレーション、理論モデル解析、実験を組み合わせて多角的に検証を行い、近年提案された2つの仮説が等価であり、実験結果とも整合することを示した。
◆本成果がゴムや関連材料を強靭化するための材料設計指針につながり、製品の薄型化と、それによる省資源化・軽量化に貢献しうると期待される。
○発表概要:
東京大学 生産技術研究所の梅野 宜崇 教授、久保 淳 助教、東京大学 大学院工学系研究科の作道 直幸 特任助教、お茶の水女子大学 理学部の奥村 剛 教授、ブリヂストンの森下 善広 研究員、角田 克彦 首席研究主幹、京都工芸繊維大学の浦山 健治 教授らの研究グループは、ゴム材料の亀裂進展速度が急激に変化する「速度ジャンプ現象」のメカニズムを明らかにしました。
速度ジャンプは古くから知られた現象であり、そのメカニズムに関してはいくつかの仮説が提案されていましたが、完全な解決には至っていませんでした。本研究では、近年提案された2種類の仮説が本質的に等価であることを示し、さらにそれらの仮説から導かれる予測が実験と良く整合することを実証しました。このようにシミュレーション・理論・実験の協奏によって、亀裂先端でのガラス転移(注1)によって速度ジャンプが引き起こされるということが明らかとなりました(図1)。
速度ジャンプ現象はゴム材料の耐久性と強い相関関係があることが知られており、そのメカニズムが明らかになったことで、ゴム材料を強靭化・高耐久化するための材料設計指針が得られると期待されます。
本研究成果は、2021年7月29日にアメリカ物理学会発行の「Physical Review Materials」のオンライン版に掲載されました。
○発表内容:
<研究の背景と経緯>
タイヤなどのゴム製品を薄型化することにより、省資源化および軽量化による低燃費性能の向上が期待できます。そのためには、素材となるゴム材料の強靭化が求められます。ゴム材料を強靭化することで、材料中に含まれる亀裂の進展速度を抑えることができ、製品の耐久性の向上に繋がります。
ゴム材料に加える外力(引裂きエネルギー)が大きいほど亀裂の進展速度が上昇しますが、引裂きエネルギーの大きさがある一定の値を上回ったときに亀裂進展速度が急激に数桁以上も上昇するということが知られており、「速度ジャンプ現象」と呼ばれます。速度ジャンプを引き起こすために必要な引裂きエネルギー(ここではジャンプエネルギーと呼ぶこととします)が大きい、つまり速度ジャンプが起きにくい材料ほど製品としての耐久性が向上することが経験的に知られていました。そのため、速度ジャンプのメカニズムを理解することで強靭なゴム材料を生み出すための材料設計指針が得られると期待されます。
1980年代に速度ジャンプ現象が初めて発見されて以来、そのメカニズムは長きにわたって謎に包まれていました。近年、久保・梅野グループと作道・奥村グループがそれぞれ独立に速度ジャンプの起源についての仮説を提案していましたが、両者の関連や実験との整合性については明らかとなっていませんでした。
<研究の内容>
本研究では、数値シミュレーション、理論モデル解析および実験を組み合わせて多角的な検討を重ねることにより、速度ジャンプ現象が亀裂先端でのガラス転移によって引き起こされるということを明らかにしました。
(1)まず、亀裂先端の力学挙動を極めて簡素化した減衰調和振動子モデル(注2)を新たに導入することで、久保・梅野グループと作道・奥村グループの先行研究によって提示されていたメカニズムが本質的に等価であるということを示しました(図2)。久保・梅野グループの先行研究では、有限要素法(Finite Element Method;FEM、注3)に基づく亀裂進展シミュレーションにより、亀裂先端での特徴的な力学的挙動が速度ジャンプを引き起こすことを見出していました。一方、作道・奥村グループの先行研究では、亀裂進展を簡素化した格子モデルによって、亀裂先端が粘性状態からガラス状態に変化することで速度ジャンプが生じるということを理論的に示していました。本研究では減衰調和振動子モデル解析により、FEMシミュレーションで観察されていた亀裂先端での特徴的な挙動が粘弾性に起因することを明らかにしました。さらに減衰調和振動子モデル解析の結果を作道・奥村グループの格子モデルと比較することで、減衰調和振動子モデルと格子モデルでの粘弾性挙動(ガラス状態・ゴム状態)に厳密な対応関係が存在することを証明しました。以上の解析結果から、減衰調和振動子モデル解析を介してFEMシミュレーションと格子モデル解析との整合性が示され、低速進展から高速進展への変化(速度ジャンプ)が生じる際に亀裂先端でガラス転移が発生することを明らかにしました。
(2)次に、FEMシミュレーションと格子モデル解析により提示された速度ジャンプのメカニズムが妥当であることを検証するために、実験との比較を行いました。FEMと格子モデルによる描像が正しいとすれば、シンプルな粘弾性材料(線形弾性(注4)、単緩和時間(注5))において次の二点が成り立つことが予測されます。
- 速度ジャンプを引き起こすために要する引裂きエネルギー(ジャンプエネルギー)は、破断時エネルギー密度に比例する。
- ジャンプエネルギーは、直接的にはガラス転移温度の影響を受けない。
これらの予測を検証するために、森下・角田・浦山グループにより、破断時エネルギー密度とガラス転移温度が異なるゴム材料に対して亀裂進展実験を実施しました。その結果、図3のように、ジャンプエネルギーと破断時エネルギー密度の間に明瞭な比例関係が成立することが示されました。またガラス転移温度が異なる3種類のゴム材料(NBR,SBR,BR)でも概ね同一の直線上にデータ点が集まっており、材料種によるガラス転移温度の違いがジャンプエネルギーに対して直接的な影響を及ぼさないことが分かりました。これらの結果は上の理論予測と良く整合しており、亀裂先端のガラス転移によって速度ジャンプが発生するという理論的描像を強く裏付けるものと考えられます。
なお、本研究は内閣府革新的研究開発推進プログラム(ImPACT)「超薄膜化・強靭化『しなやかなタフポリマー』の実現」による支援を受けて実施されました。
<社会的な意義>
ゴム材料の破壊現象に対する理解が進むことで、より強靭な材料を開発するための指導原理が得られると期待できます。また、本研究の議論は一般的な粘弾性に基づいているので、ゴム以外の材料(ゲルなどのソフトマター)の破壊現象にも広く適用できると考えられます。
○発表雑誌:
雑誌名:Physical Review Materials(オンライン版:7月29日)
論文タイトル:Dynamic glass transition dramatically accelerates crack propagation in rubberlike solids
著者:Atsushi Kubo*, Naoyuki Sakumichi, Yoshihiro Morishita, Ko Okumura, Katsuhiko Tsunoda, Kenji Urayama, Yoshitaka Umeno
DOI番号:10.1103/PhysRevMaterials.5.073608
○問い合わせ先:
東京大学 生産技術研究所
教授 梅野 宜崇(うめの よしたか)
○用語解説:
(注1)ガラス転移
高分子材料におけるガラス転移とは、ガラス状態からゴム状態に(あるいはゴム状態からガラス状態に)変化すること。ガラス状態では分子の運動が強く拘束されているため変形しにくいが、分子の拘束が弱いゴム状態では容易に変形できる。ゴム材料は常温では文字通りゴム状態であるが、温度を下げたり急激な変形を加えたりするとガラス状態に転移する。一般にガラス転移によって弾性係数(材料の硬さ)は数百~千倍程度も変化する。
(注2)減衰調和振動子モデル
質点に線形のバネとダッシュポットを接続した力学モデル。材料の粘弾性を表現する際に用いられ、減衰振動などの運動を表現できる。バネとダッシュポットの個数や繋げ方によって、モデルのバリエーションがある。
(注3)FEM解析
連続体上の微分方程式を解くための数値解析手法の一つ。対象の領域を細かな要素に分割し、各要素に対して方程式を解くことで、領域全体での解を求めることができる。本研究では応力やひずみといった力学的な場を扱ったが、他にも電磁場や流体などのさまざまな対象に適用される。
(注4)線形弾性
変位と力の間に比例関係(フック則)が成り立つこと。また、弾性論において、ひずみと応力の間に線形関係(一般化フック則)が成り立つこと。比例係数は弾性係数などと呼ばれ、材料によって決まる物性値である。
(注5)緩和時間
粘性が影響を及ぼす時間の長さのこと。粘性係数と弾性係数の比として計算される。単緩和時間とは、材料の粘性挙動が単一の緩和時間によって表されることを指す。現実の高分子材料の緩和メカニズムは複雑なため、緩和時間は単一ではなく広がり(緩和スペクトル)を持つ。
○添付資料:
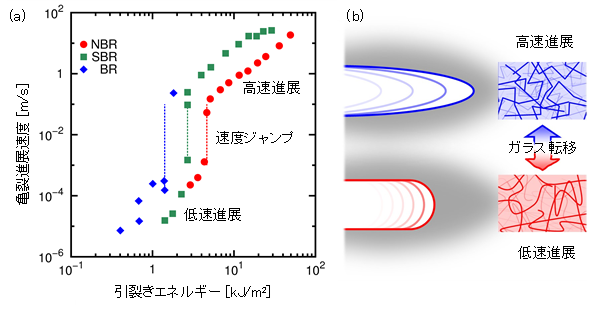
図1 (a) 亀裂進展速度と引裂きエネルギーの関係。さまざまな種類のゴム材料(NBR, SBR, BR)で、引裂きエネルギーがある値(ジャンプエネルギー)に達すると急激に増大する「速度ジャンプ」が見られる。(b) 本研究では速度ジャンプが亀裂先端でのガラス転移に起因することを明らかにした。
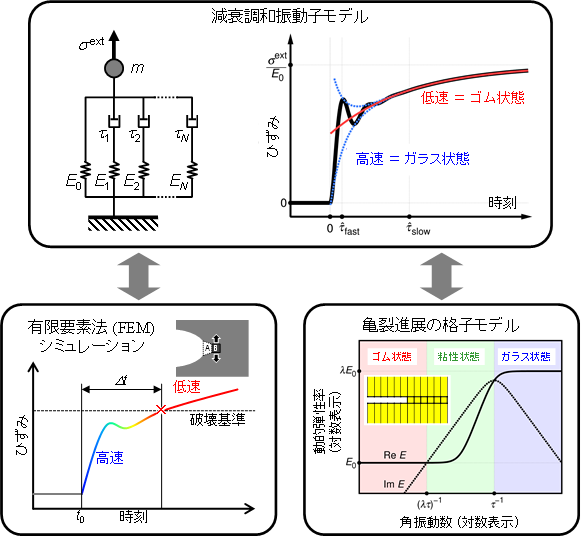
図2 減衰調和振動子モデルとFEMシミュレーション、格子モデルとの関係。減衰調和振動子モデルを介して、FEMシミュレーションと格子モデルとの明確な対応関係が示される。
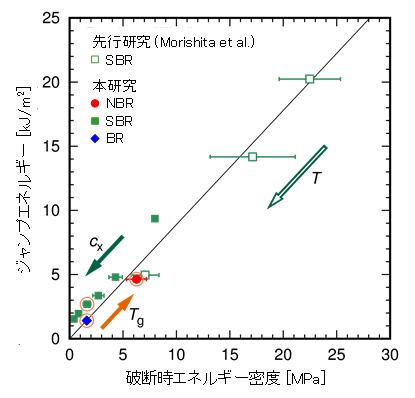
図3 ジャンプエネルギーと破断時エネルギー密度の関係。実験パラメータ(cx, Tg, T)の値を変化させても、全てのデータ点がほぼ直線上に位置している。先行研究(白抜きの点)はMorishita et al. Polymer 108 230-241 (2017) による。