(“Liquid” machine-learning system adapts to changing conditions)
2021/1/28 アメリカ合衆国・マサチューセッツ工科大学(MIT)
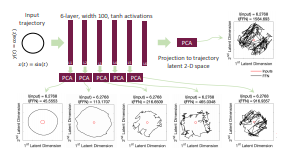
・ MIT が、トレーニング時以外も継続して学習し、変化する現実のシステムに適応する新タイプの「リキッド(可変的な)」回帰型ニューラルネットワーク(RNN)を開発。
・ 方程式を変えて新しい入力データに連続して適応するフレキシブルな学習アルゴリズムにより、医療診断や自動運転のような経時的に変化するデータストリームに基づいた意志決定を促進する。未来のロボット制御、自然言語処理や動画処理等の、あらゆる形態の時系列データ処理を進展させる大きな可能性を提供する。
・ 動画処理、金融データや医療診断アプリケーションは、社会の中核を成す時系列の一例。これらのような継続して変化するデータストリームの変動は予測が不可能だが、これらのデータをリアルタイムに分析して未来予測が可能となれば、自動運転車のような新興技術の開発促進が見込める。
・ ニューラルネットワークは、一連の「トレーニング」の実例を分析することでパターンを認識するアルゴリズムであり、脳の情報処理経路を模倣したものとも言われる。新 RNN は、僅か 302 個のニューロン(神経細胞)でも予想外の複雑な動態を示す線虫に着想を得た。
・ 新 RNN では、繰り込まれた一連の微分方程式をベースに、パラメータの経時的な変化を可能にした。NN の多くではトレーニング後に挙動が固定化され、入力データストリームの変化への対応が不可能。新 RNN の流動性は、予想外のデータやノイズの多いデータに柔軟に対応できる。
・ 新 RNN の柔軟性は、他の NN に共通した不可測性を回避する利点も提供。表現力の極めて高い少数のニューロンで、ネットワークによる意志決定の「ブラックボックス」の解明を容易にした。
・ 新 RNN は、様々な試験において優れた結果を提示。大気化学からトラフィックパターンに至るまで、データセットの正確な数直予測において他の最先端の時系列アルゴリズムの性能を数パーセントポイント上回った。また、サイズが小型のため、コンピューティングコストの上昇も抑える。
・ 未来のインテリジェントシステムの主要な要素として、自然に着想を得たより表現力を向上させた新RNN の拡張方法が今後の課題。産業アプリケーションに向けた改善を続ける。
・ 本研究には、ボーイング、米国立科学財団(NSF)、オーストリア科学財団(FWF)および Electronic
Components and Systems for European Ladership(ECSEL)が一部資金を提供した。
URL: https://news.mit.edu/2021/machine-learning-adapts-0128
<NEDO海外技術情報より>
(関連情報)
arXiv.org (コーネル大学図書館)公開論文(フルテキスト)
Liquid Time-constant Networks
URL: https://arxiv.org/pdf/2006.04439.pdf
Abstract
We introduce a new class of time-continuous recurrent neural network models. Instead of declaring a learning system’s dynamics by implicit nonlinearities, we construct networks of linear first-order dynamical systems modulated via nonlinear interlinked gates. The resulting models represent dynamical systems with varying (i.e., liquid) time-constants coupled to their hidden state, with outputs being computed by numerical differential equation solvers. These neural networks exhibit stable and bounded behavior, yield superior expressivity within the family of neural ordinary differential equations, and give rise to improved performance on time-series prediction tasks. To demonstrate these properties, we first take a theoretical approach to find bounds over their dynamics, and compute their expressive power by the trajectory length measure in a latent trajectory space. We then conduct a series of time-series prediction experiments to manifest the approximation capability of Liquid Time-Constant Networks (LTCs) compared to classical and modern RNNs.



