電子らせん波の形状を初観測～電子らせん波の新たな計測法への展開に向けて～

2020-02-142021-09-10

2020-02-14 理化学研究所

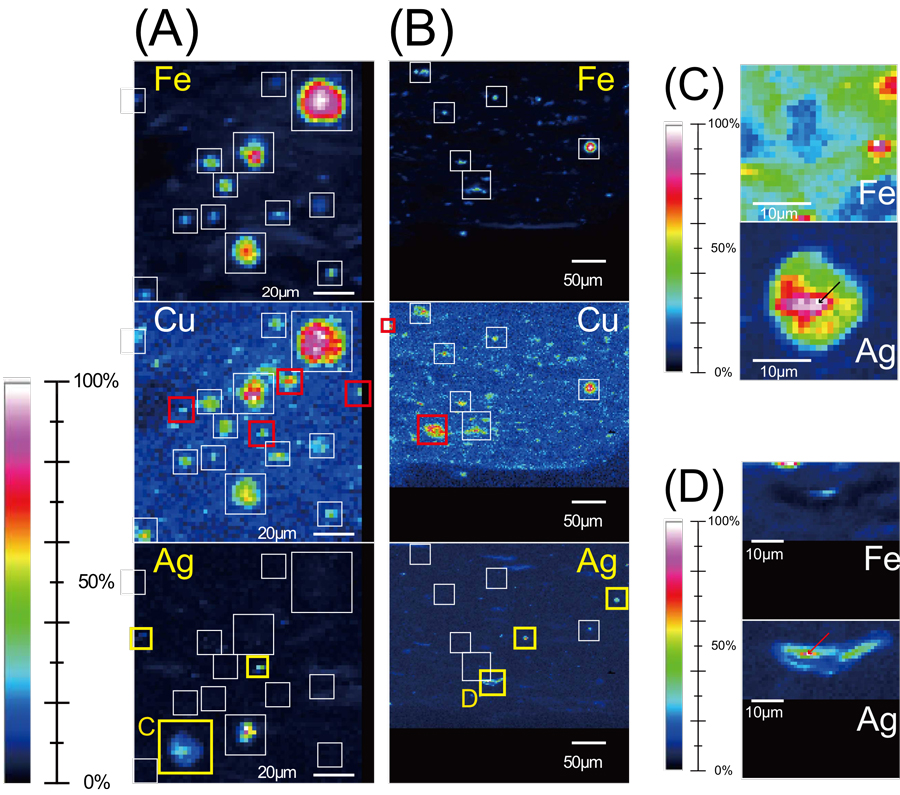
理化学研究所（理研）創発物性科学研究センター創発現象観測技術研究チームの原田研上級研究員らの研究チームは、電子線ホログラフィー^[1]の技術を用いて、電子波の等位相^[2]面（波面^[2]）がらせん形状を成す「電子らせん波」の形状を観測することに成功しました。

本研究成果は、材料特性・構造解析・加工法に新たな可能性をもたらすと期待されている電子らせん波の物性を明らかにするもので、次世代の荷電粒子線装置の開発に貢献すると期待できます。

今回、研究チームは、電子波が「刃状転位格子^[3]」とその周辺部を透過できる半透明膜を用いたらせん波生成法を採用しました。これにより、従来は回折パターンとして強度像のみを得ていたらせん波を、格子周辺を透過した電子波との干渉パターン（ホログラム^[4]）として記録し、そのホログラムから電子らせん波の振幅^[2]分布と位相分布の再生に成功しました。その結果、電子らせん波は伝搬方向に方位回転を伴って伝搬していることを確認しました。これまで、電子らせん波の強度分布が空間的にねじれていることは、回折パターンの計測から知られていましたが、振幅分布と位相分布がそれぞれ伝搬方向にねじれていることが確認されたのは初めてです。

本研究成果は、日本応用物理学会の速報誌『Applied Physics Express』のアクセプト版（1月27日付）、オンライン版（2月11日付）に掲載されました。

電子線ホログラフィーにより再生された四つの電子らせん波像（色は位相、輝度は振幅を示す）

背景

光波など伝搬する波動^[2]の位相は、一般には一意に決定されます。このとき、等位相面（波面）の形状により、波は平面波、球面波などに分類されます。一方、等位相面に特異点^[5]がある場合、位相が一意に決定されない波が存在します。その代表が「らせん波」です。らせん波は、その名の通り特異点を軸としたらせん形状の波面を持ちます。

電子線で作られるらせん波である「電子らせん波」は、軌道角運動量^[6]を持って伝搬すると考えられています。軌道角運動量は、らせん波の中心に集中しており、トポロジカル数^[7]で表されます。トポロジカル数は整数で、らせん波の巻き数に対応しており、正負の符号はらせん波の右巻きか左巻きかに対応しています。

図1に、平面波と平面状らせん波を示します。aは平面波、bはトポロジカル数が+1のらせん波、cはトポロジカル数が+2のらせん波です。b、cでは、波面の中央にらせん軸があり、この軸を周回すると、bでは波面がちょうど1波長分（位相差2π）だけ、cでは2波長分（位相差4π）だけずれます。波面形状のひずみは、らせん軸、すなわち特異点に集中しています。

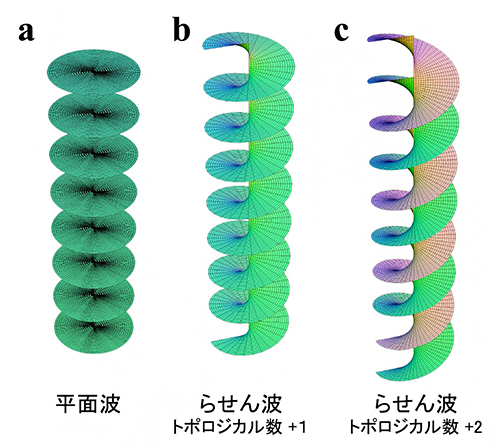
図1 平面波と平面状らせん波

a:平面波では、等位相面（波面）が平面である。

b:平面状らせん波（トポロジカル数+1）：らせん軸を方位角が周回すると、1波長分（位相差2π）だけ位相面がずれる。なお、ここでは平面状のらせん波を描いているが、球面波や円錐波のらせん波も存在する。

c:平面状らせん波（トポロジカル数+2）：らせん軸を方位角が周回すると、2波長分（位相差4π）だけ位相面がずれる。波長は一定でなければならないため、2枚の波面によるモデルが考えられている。

電子らせん波をプローブとして用いることにより、荷電粒子線装置の新しい応用分野が開拓されると期待されています。例えば、磁気構造の観察において、従来の電子線では電子線に平行な磁束は検出できませんが、電子らせん波では軌道角運動量による磁束の検出が期待されています。さらに、微細加工や磁化制御への応用にも、その可能性が検討されています。

今回、研究チームは、電子線ホログラフィーの技術を用いて、電子らせん波の形状観察を試みました。

研究手法と成果

研究チームは、電子らせん波を生成させるために「刃状転位格子」または「フォーク型格子」と呼ばれる格子を用いる方法を採用しました。図2に、刃状転位格子を用いたらせん波生成の概略を示します。平面波を刃状転位格子に照射すると、格子を通過した後の波は、そのまま通過した平面波と、格子の左右に回折し、各々逆の巻き方をした（正負反対のトポロジカル数を持つ）らせん波となります。らせん波のトポロジカル数は、刃状転位格子の次数と回折次数^[8]の積となります。例えば、図2のように3次の刃状転位格子を使用した場合、トポロジカル数は±１次の回折波（らせん波）では±3、±2次の回折波（らせん波）では±6となります。

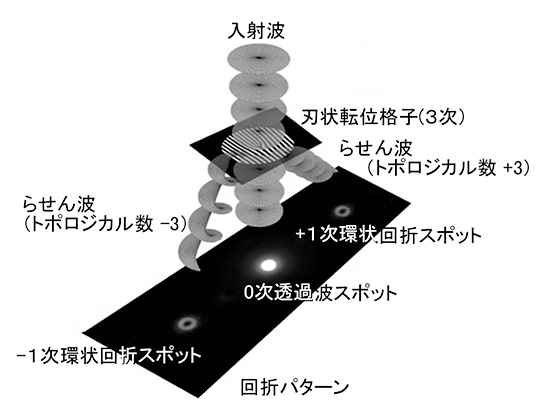
図2 刃状転位格子を用いたらせん波の生成

平面波が刃状転位格子に入射すると、その回折波はらせん波となって伝搬する。らせん波のトポロジカル数は、刃状転位格子の次数と回折次数の積となる。この図では、3次の刃状転位格子のため、トポロジカル数は±1次の回折波（らせん波）で±3となる。また図示はしていないが、±2次の回折波（らせん波）では±6となる。

今回開発した手法は、半透明の膜に刃状転位格子を作製し、格子よりも広い範囲に電子波を照射します。電子らせん波の観察は、回折パターンの観察位置ではなく、上下いずれかの方向にずらした位置で観察するという構成を特徴としています。図3に、ホログラム記録光学系を示します。電子波を格子よりも広い範囲（格子の開口径の10倍）に照射することで、回折パターン面では1点に収束していた0次透過波（参照波源）は回折点から急速に広がり、回折パターン面の上下で回折波、すなわち、らせん波と重なり、干渉パターン（ホログラム）を作ります。

本手法は、観察試料により散乱を受けた波と試料の周辺部を透過した波との干渉をホログラムとして記録するという点では、デニス・ガボールによるホログラフィー^[4]発明のオリジナルアイデアと同じです。しかし、試料から回折を受けた単独のらせん波と格子周辺部を透過した波との二つの波動の干渉（二波干渉）のホログラムであることから、従来の電子線ホログラフィーの技術がそのまま適用可能という利点があります。

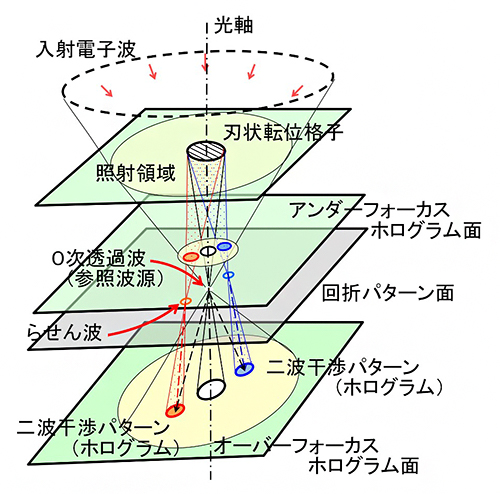
図3 電子らせん波のホログラム記録光学系

刃状転位格子を含む周囲の広い領域に電子波を照射することを特徴とする。入射波の収束位置が回折パターン面となり、らせん波がリング状スポットとして観察される。回折パターン面の上方、もしくは下方において、0次透過波（参照波）と回折波（らせん波）との重なった畳領域に発生した二波干渉パターンをホログラムとして記録する。

図4左に、5次の刃状転位格子を用いて、観察されたらせん波のホログラム（強度像）を示します。±1次と±2次の回折波による四つの干渉像（リング状スポット）が観察されました。各々のリング状スポットがらせん波で、リングにいくつも重なった縦方向の干渉縞がホログラムであることを示しています。

このホログラムからの再生像を図4右に示します。上段（a-b）が±1次のホログラムより再生されたトポロジカル数±5のらせん波、下段（c-d）が±2次のホログラムから再生されたトポロジカル数±10のらせん波の像です。振幅像は輝度で、位相像は色でそれぞれの値を表示しています。振幅像の2乗が強度像になるため、振幅像はホログラムの強度像と似たリング状となっています。位相像は、リング状スポットの内側までプロペラ状の分布を示し、波面がらせん形状を成しており、これはらせん波が再生されたことを示しています。この結果により、ホログラムから電子らせん波の再生が成功したことが分かりました。なお、この四つのデータを合成したものが1ページ目の図です。

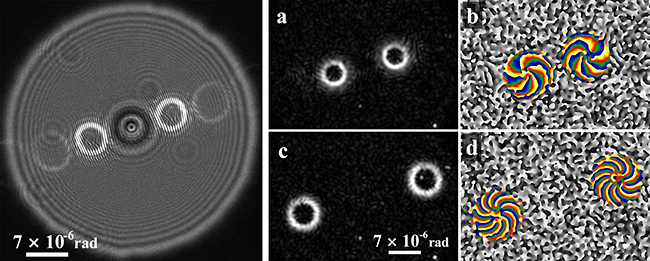
図4 電子らせん波のホログラムと再生された振幅像と位相像

左:5次の刃状転位格子を用いて、±2次までの回折波を記録したホログラム（強度像）。

右:aは1次回折波から再生された振幅分布像、bは1次回折波から再生された位相分布像、cは2次回折波から再生された振幅分布像、dは2次回折波から再生された位相分布像。1次回折波からのらせん波はトポロジカル数±5、2次回折波からのらせん波は±10である。

従来は、リング状スポットのひずみや輝度の変化に基づいて、らせん波を強度像として観察していました。本手法では、ひずみや輝度の変化に加えて、らせん形状を成す位相分布のずれからも、らせん波の状態を知ることができます。そのため、試料や試料による電磁場を透過してらせん波の位相分布に変調が生成した場合には、その変調を通して試料の状態を知ることができます。

ホログラフィーでは、伝搬する波動の全情報を記録・再生できるため、らせん波でも伝搬する途中の波動を追跡して表示することができます。図5に、3次の刃状転位格子から生成した三つの異なる空間でのらせん波の再生振幅像と位相像を示します。中段（c-d）はホログラム面（回折パターン面）、上段（a-b）と下段（e-f）はホログラム面の上下に光学的にそれぞれ25mm離れた位置における、±1次の回折波の再生像です。

上段（a-b）は、左側にある-1次回折波にとって刃状転位格子位置での波動場（刃状転位格子に焦点が合った条件）に該当します。振幅像aは、平面状に再生され（特異点であるらせん軸近傍では、振幅値はほぼゼロになっている）、位相像bでは3枚のプロペラからなるファン形状を成したらせん状の波面が再生されています。一方、右側にある+1次の回折波にとっては、ホログラム面よりもさらにフォーカスが外れた位置での再生像に該当しています。

中段（c-d）は、振幅像、位相像ともに左右のらせん波は等価な分布をしており、下段（e-f）は、右側にある+1次回折波にとって刃状転位格子位置での再生像となっています。

図5 伝搬経路上の電子らせん波の振幅分布と位相分布の再生像

a-b: 左側の-1次回折波について、左側の刃状転位格子位置（刃状転位格子に焦点が合った状態）での再生振幅像と位相像。右側の+1次回折波については、逆に焦点はずれ量が増大している。

c-d: ホログラム記録位置での再生振幅像と位相像。左右の回折波は、同じ焦点はずれ状態で再生されている。

e-f: 右側の+1次回折波について、右側の刃状転位格子位置（刃状転位格子に焦点が合った状態）での再生振幅像と位相像。左側の-1次回折波については、焦点はずれ量が増大している。

以上のように、電子らせん波のホログラムを記録することで、振幅像と位相像を再生すること、そしてホログラフィーの再生技術を利用して、刃状転位格子を配置した位置からホログラムを記録した位置までの任意の空間の電子らせん波を再生することに成功しました。これにより、振幅像と位相像の両方が、伝搬方向に回転していること、すなわち、振幅と位相の両分布がねじれながら伝搬していることを初めて確認しました。

今後の期待

今回開発した電子線ホログラフィーにより、電子らせん波の波面が直接計測できるようになったため、らせん波が試料材料やその電磁場状態から受ける変調を、より高精度に検出できると考えられます。これにより、電子らせん波を計測に用いる具体的な技術・装置に発展させられると期待できます。

さらに本手法が、これまで実現できていなかった回折空間での電子線ホログラフィーを実現できる技術に発展させられると確信しています。今後、らせん波を用いた応用研究だけでなく、本手法を発展させて、電子線ホログラフィーの回折空間への展開も目指していきたいと考えています。

補足説明

1.電子線ホログラフィー
電子顕微鏡で電子線（電子波）を用いて実施されるホログラフィー技術のこと。一般には、電子線バイプリズムと呼ばれる波面分割装置を用いて、試料のインフォーカス像（焦点が合っている像）に対してホログラムを記録・再生する。電子と相互作用するものであれば、位相分布として再生像での観察が可能で、アハラノフ・ボーム効果の検証や超伝導磁束量子の観察など、物質・材料以外の電磁場分布についても観察例がある。

2.波動、振幅、位相、波面
「波動」は、例えば水面に生じる波紋のように、ある媒質の振動（山と谷の状態を繰り返す）として考えられる。その振動のうねりの大きさを「振幅」、振幅の変動する様子を「位相」と呼ぶ。波動は一般に、この振幅と位相とで表現される。また、振幅が山の状態の部分、あるいは谷の状態の部分をつないだ、位相のそろった面（等位相面）を「波面」と呼ぶ。波動を伝える媒質は、水波の場合には水であり、光の場合には電磁場である。電子波の場合には、電子の存在する確率密度であると考えられている。一般に記録される波動の情報は、振幅の2乗である強度分布のみであり、位相分布は記録できない。そのため、ホログラフィーなどの技術が開発されている。

3.刃状転位格子

回折格子の格子面内の一部に、格子（棒）が余分に刺し込まれたタイプの格子のこと。余分に挿入された格子の本数が1本の場合が1次の刃状転位格子、3本の場合が3次の刃状転位格子である。この形状が食器のフォークに似ていることから、近年はフォーク型格子とも呼ばれている。

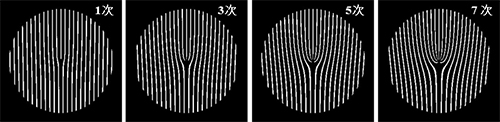
次数の異なる刃状転位格子（フォーク型格子）

4.ホログラフィー、ホログラム
「ホログラフィー」は、波動場の干渉を利用して、その波動の振幅分布と位相分布の両方を同時に記録・再生できる手法。1947年にデニス・ガボールによって発明された。一般には、レーザー光を用いた立体像を得る写真技術として知られている。試料を透過したり、試料で散乱を受けた波動（物体波）と、試料から離れた位置を通過して散乱を受けなかった波動（参照波）を重ねて干渉させ、その干渉パターンを記録したものを「ホログラム」と呼ぶ。このホログラムには、物体波の振幅分布と位相分布が完全に記録されているため、既知の参照波の情報をもとに実験的、あるいは理論的（計算的）に、物体波の全情報（振幅分布、位相分布）を再生することが可能である。

5.特異点
一般的な手順、基準では求まらない特別な点、あるいは一般的な基準を適用できない点のこと。らせん波では、らせん軸は波面が描けない特異点である。また、ブラックホールの中心は、物質の密度が無限大になる領域であり、時空の特異点である。

6.軌道角運動量
物体の円運動により導かれる角運動量のこと。らせん波を粒子のモデルで考えると、電子がらせん軌道を描きながら飛んでいるようなイメージで置き換えられ、磁場を付随させながら伝搬していく電子波がイメージされるが、これはらせん波の回折パターン（強度）がリング状スポットとになっていることからも正しくない。しかし、らせん波における位相変化の特徴より、電子の円運動に付随する角運動量がらせん軸に付随して伝搬していく波動がイメージされる。

7.トポロジカル数
位相幾何学でいう渦を特徴づける「巻き数」に相当する数のこと。渦の形状が変わっても同じ値を保って変化せず、整数値をとる。

8.回折次数

回折波の次数。0次の透過波（散乱を受けなかった波）に対して、格子により散乱（回折という）を受けた波が格子間隔とその方位に応じて干渉した結果1点に集まる。その0次スポットからのスポット数に応じて、±1次、±2次、±3次…と名付けられている。下図のように本研究に使用した刃状転位格子の場合には1列だが、実際の結晶では、2次元に格子が分布するため、回折パターンも2次元に配列する。