2019-11-26 東京大学
大塚 孝治(東京大学名誉教授
/理化学研究所仁科加速器科学研究センター 核分光研究室 客員主管研究員)
角田 佑介(原子核科学研究センター 特任研究員)
阿部 喬(原子核科学研究センター 特任助教)
清水 則孝(原子核科学研究センター 特任准教授)
Piet Van Duppen(ルーバン大学 教授)
発表のポイント
- 重い原子核は球から楕円体に変形し、それが回転して回転バンドを作る。回転バンドを、スパコンでのモンテカルロ殻模型計算により、有効核力で相互作用する核子多体系のシュレーディンガー方程式の解として初めて求めた。2つの典型例に対し理論計算を行い、実験データとの一致をみた。一つの原子核で2、3番目などの回転バンドは、伝統的にはベータ振動やガンマ振動を表すとされている。それは、A. ボーアのノーベル賞受賞講演(1975年)で強調され、多くの教科書に既定事実のように書かれている。しかし、この計算はそれらの回転バンドは異なる構造的特徴を持つことを示した。
- 新たな基本メカニズムを提案した。伝統的には、直接変形を起こす力(四重極相互作用)が特に重要とされてきたが、それでは不十分であることを示した。変形への抵抗をコントロールするモノポール力の効果を指摘し、スパコンでの計算で実証した。自己組織化での秩序 (order) の形成に相当し、その結果として新しい構造が出現する。
- 本研究成果は、従来の定説を覆して、超重元素の原子核を含め、今後の原子核研究に大きなインパクトを与える。重い原子核は宇宙での元素合成に関わり、放射性廃棄物になるものもあるので、適切な理解は有用である。本研究成果は、Physical Review Letters 誌に掲載決定され、特にEditors’ Suggestion に選ばれた。
発表概要
多くの原子核では表面の形は球ではなく変形して楕円体となる(注1)。原子核の古典的モデルである液滴模型で、液滴が球から楕円体に変形することに対応する。A. ボーア と B.R. モッテルソン(ノーベル賞受賞講演など)は、原子核の基底状態(エネルギーが最低の最も安定な状態)がある楕円体になっている場合、楕円体の一番長い軸方向に表面が振動(ベータ振動)、あるいは、短い軸方向に振動(ガンマ振動)するモードを提唱した。それらは、2番目、3番目などの励起回転バンドとして現れるとされ、既知のこととして教科書に示されてきた(図1)。一方、これまでの微視的な理論計算では、それらの満足のいく記述はなかった。
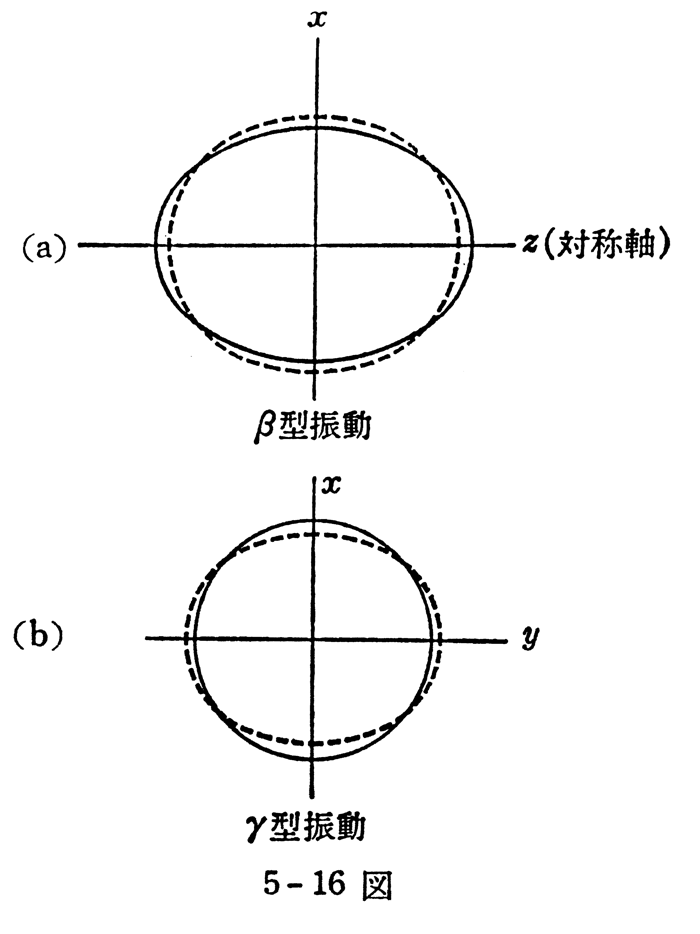
図1:ベータ振動とガンマ振動の模式図。野上茂吉郎著「原子核」(裳華房 基礎物理学選書 13巻、143ページ、5−16図)より転載。楕円体の一番長い軸をz 軸とし、それは (a)では横方向に, (b) では紙面に垂直な方向に向いている。
ポスト「京」重点課題9(注2)に参加している東京大学・理化学研究所のグループは、同グループが推進してきたモンテカルロ殻模型計算(注3)による大規模並列計算を、スーパーコンピュータ「京」やオークフォレスト・パックスのような大型スパコンを用いて行い、この難問に挑戦した。サマリウム-154 (154Sm) やエルビウム-166 (166Er) のような典型例に対し、適切な有効核力を入力として、かつてない大規模なモンテカルロ殻模型のシミュレーション計算を遂行し、実験とよく一致する結果を得た。しかしながら、得られた結果を分析すると、ベータ振動/ガンマ振動に基づく伝統的な考え方とは全く異なっていた。
回転バンドの形成では、四重極モーメントを大きくして楕円体を作ろうとする四重極相互作用が強く働き、従来の研究ではそれに着目していた。この研究では、それだけでは不十分であり、加えて、単極(モノポール)相互作用が量子系に特有の離散的一粒子状態エネルギーを変化させ、注目している回転モードに最適化して、変形に対する抵抗(力)を弱めるメカニズムを指摘した。さらにその重要性をスパコンでの計算で実証した。これは外場の変化に対して、無秩序(disorder) から秩序 (order) に変化する自己組織化の一つの現れであると言える。すなわち、陽子と中性子という2種類の粒子がお互いに相手に対して外場のように振る舞うのである。四重極相互作用は変形を陽に推し進め、単極相互作用は直接変形には結びつかないものの、抵抗を弱めて実際には大きな効果を生む。分かりやすく表現すれば、単極相互作用は多くの粒子が変形の増大に関われるように環境を整える、という言い方もできる。これはまさに、自然科学から社会科学まで広い分野で見られる自己組織化と共通の本質を持つ事象である。このことは従来見落とされていたが、多体系の多くの場合に関わり得るものである。
自己組織化メカニズムは原子核が重くなるほどに効果が増すので、ウランや超重元素の原子核ではさらに効果を増し、超重魔法数にも影響を与える。重い原子核は中性子星合体で起こる「 rプロセス(注4)」での中間生成物であり、重い原子核のより正確な理解は重要である。
発表内容
原子核は多数の核子から成るので、個々の粒子としての性質が反映されるのは当然である。一方、多数の粒子がお互いに相関を持って動けば、集団的に揃った運動モードが発現する。一粒子的な側面が強いと、このような集団モードの発展は阻害される。そこで、一粒子状態と集団モードの関係は、原子核が量子力学的に扱われるようになって以来存在し続け、重要で未解決の部分を含む問題である。この事は A. ボーアとB.R. モッテルソンの権威ある教科書で指摘されている。また、長く分野のリーダーであり近年亡くなった G.E. ブラウンもずっと胸に抱き続けていた基本的問題であった。
ポスト「京」重点課題9に参加している東京大学を中心とするグループはモンテカルロ殻模型計算による大規模並列計算により、この難問に挑んだ。規模の大きさから実行が困難な計算であったが、実験データとよく合う結果を得て、その背後にある未知の構造を明らかにした。図2に研究成果のうち、サマリウム-154に関するものの一部を示す。パネルaは実験データで、パネルbは今回の計算値である。両者はよく一致している。この研究は、ベルギーのルーバン大学の研究者と共同で行った。
このような一致が得られた理由は、変形を起こすメカニズムにある。伝統的には、核子(陽子と中性子の総称)が多数活性化された場合に、有効核力の一成分である四重極相互作用が強く働いて、四重極変形を増大させ楕円体を成すと考えられてきた。この研究では、それに加えて、核力の別の成分である単極(モノポール)相互作用が、考えている回転バンドごとに、量子系に特有の離散的一粒子状態エネルギーを変え(最適化して)、変形に対する抵抗を弱めると予想した。さらに大規模計算でそれを実証した。図2のパネルcには、この最適化メカニズムが2番目のバンドに対しては働かないようにした結果を示す。励起エネルギーが上がってしまって実験との一致が失われているのが分かる。
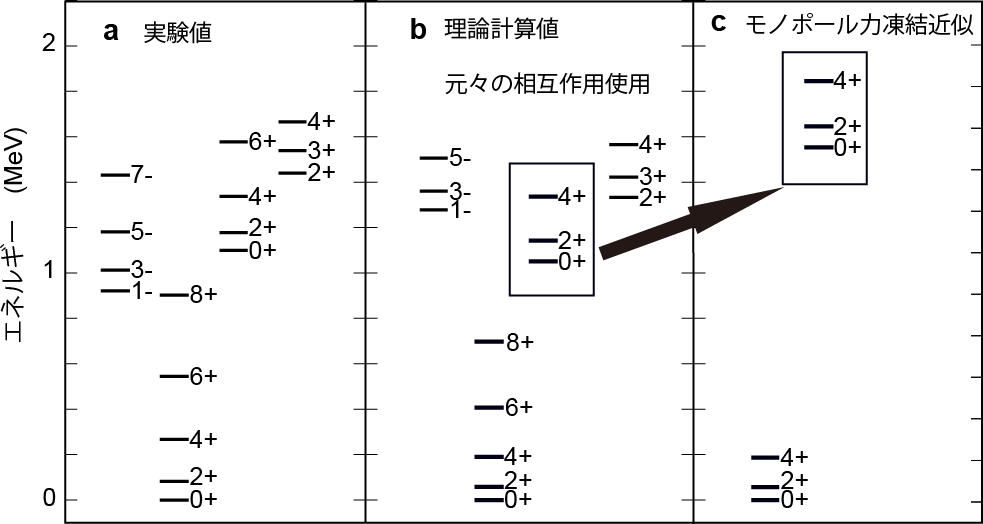
図2:サマリウム−154 のエネルギーの低い4種類の回転バンドを左から右へ並べたもの。パネルa はそれらの実験値、パネル b は今回の理論計算の結果を示す。パネル c では、パネル b の左から3番目のバンド(中央部の四角い枠内)に対し単極(モノポール)力の効果を消した(凍結した)計算の結果を表す(パネル c の中央部上寄りの四角い枠内)。
各々の回転モードは異なる形に対応するので、形ごとに一粒子状態エネルギーを最適化する、つまり秩序 (order) が形成されることになり、項目3で述べたように自己組織化の一つの現れである。核力が豊かな構造を持っている帰結であり、多様な結実が期待される。それは、L.D. ランダウのフェルミ液体論で想定されているような、固定された入れ物の中のほとんど自由な核子群という見方からは違っている。
エルビウム−166 に対する計算では、ガンマ振動の実験的証拠として A. ボーアが指摘したデータが、そのような模型的仮定をしなくても計算して得られていることが示された。一方、得られた構造は伝統的なものとは異なる、ソフトな非軸対称変形と呼ばれるものである。
原子核が重くなるほどに、関与する一粒子状態の数が増え、活性化された核子の数も増えるので、自己組織化メカニズムは効果が大きくなる。つまり変形を起こす環境がよりテイラーメードになるのである。そこで、重いウランや超重元素の原子核でのさらに大きな効果が予見され、超重魔法数がどのように決まるか、どの数になるか、にも影響を与えるのは確実である。
重い原子核は中性子星合体で起こる rプロセスでの中間生成物であり、原子炉内での核分裂生成物でもあるので、重い原子核のより確実な理解は重要である。また、ベータ振動やガンマ振動は核分裂の途中の経路で重要な役割を果たすと言われてきた。ベータ振動やガンマ振動が明確なモードとしては現れなくなると核分裂のシナリオに変化を起こすと考えられる。さらに、本研究ではエネルギー面極小点(local minimum)が所々に現れると予想されており、それらの極小点をトンネル効果でつないだプロセスと核分裂の関係、と言うような新しい見方も今後研究されていくであろう。このように、本研究で示されたメカニズムは大変幅広い裾野を持っていると考えられる。
本研究成果はPhysical Review Letters 誌に掲載予定で、掲載論文から重要度の高いものに授与されるEditors’ Suggestion に選ばれた。Physical Review Letters 誌のホームページで論文とは別に紹介され、そこで使われる予定のイメージ図を図3に示す。この研究の成果の独創的な点を端的に表し、伝統的な描像とは異なる。
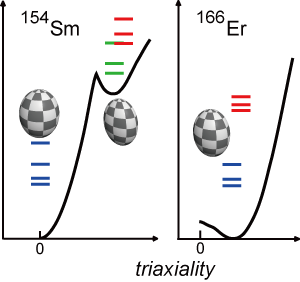
図3:Physical Review Letters 誌の Editors’ Suggestion で説明に使われる予定のイメージ。triaxiality は注1を参照。
本研究は、大塚孝治東京大学名誉教授(理化学研究所仁科加速器科学研究センター核分光研究室客員主管研究員)、東京大学大学院理学系研究科角田佑介特任研究員、阿部喬特任助教、清水則孝特任准教授、ルーバン大学Piet Van Duppen教授のメンバーによって実施された。
本研究は、文部科学省ポスト「京」重点課題9「宇宙の基本法則と進化の解明」および計算基礎科学連携拠点(JICFuS)の元で実施したものである。また、本研究成果は、理化学研究所のスーパーコンピュータ「京」(課題番号:hp160211, hp170230, hp180179, hp190160)および最先端共同HPC基盤施設のスーパーコンピュータ「オークフォレスト・パックス」によって得られたものである。
発表雑誌
- 雑誌名
Physical Review Letters論文タイトル
Underlying structure of collective bands and self-organization in quantum systems著者
Takaharu Otsuka*, Yusuke Tsunoda, Takashi Abe, Noritaka Shimizu, Piet Van DuppenDOI番号
10.1103/PhysRevLett.123.222502
用語解説
注1 多くの原子核では表面の形は球ではなく変形して楕円体となる
原子核は形を持つ。それは球や楕円体である。球を基準として楕円体などになるのを変形という。原子核を液滴のようなものと考えれば、表面張力で球になると考えられるが、実際には変形している原子核の方が多い。変形にはがっちりした堅いものと、ぶよぶよした柔らかいものがある。量子論的には、陽子と中性子の間の核力の短距離での強い引力が原因で変形が起こると考えられる。 楕円体には軸が3本あり、その中の最も長いのが1本の場合に、残りの2本の長さが等しいと軸対称、逆に差がゼロでないと非軸対称と呼ぶ。従来の見方に反して、今回の研究では非軸対称変形が多くの回転バンドで起きていることも分かった。図3の triaxiality とはこの非軸対称性を表す。
注2 ポスト「京」重点課題9
2020年頃から始まるスーパーコンピュータ・ポスト「京」(富岳)運用に向けて、素粒子・原子核・宇宙物理分野の研究のための精密計算およびシミュレーションコードの開発を目的としたプロジェクト。スーパーコンピュータを用いた大規模計算により、素粒子から宇宙まで桁違いのスケールにまたがる現象の研究を行っており、大型実験・観測データと組み合わせて物質創成史の解明を目指している。
注3 モンテカルロ殻模型
原子核の中の多数の陽子と中性子から成る多体系の量子構造を解明する方法の一つ。他の分野でCI (Configuration Interaction)計算と呼ばれる方法と原子核物理での殻模型計算は本質的には同じである。モンテカルロ殻模型は殻模型計算に含まれるが、通常の方法では扱えない非常に大きな系も扱える。東京大学を中心に発展してきた。
注4 rプロセス
宇宙での爆発的現象で元素合成が行われるプロセスの一つ。中性子星合体や超新星爆発で短時間の間に大量に発生する中性子が星の中にある原子核に当たり、中性子過剰な不安定核を生成する。それのベータ崩壊と、さらなる中性子の捕獲が競争し、それらが何回も起きながら進行するプロセスである。鉄より重い原子核の生成プロセスとして重要である。本研究で例として取り上げられた原子核にさらに数個の中性子を加えると、rプロセスに関与する原子核になるので、原子核の CI計算の守備範囲になりつつあると言える。
―東京大学大学院理学系研究科・理学部 広報室―