「会合比はいくつか？」～1884年のファントホッフの手法が現代化学の難題の解法に～

2023-12-222024-09-12

2023-12-21 東京大学

池本晃喜（化学専攻准教授）
磯部寛之（化学専攻教授）

発表のポイント

複数の分子が弱い相互作用により会合する超分子錯体が、どのような会合比から出来ているのかを解明する手法を開拓しました。1884年にファントホッフが提案した「ファントホッフ・プロット」（第1回ノーベル化学賞）が、おおよそ140年後の現代、超分子化学分野での難題の解法となることを発見したものです。
「超分子錯体の会合比の決定」は、過去1世紀近くの間、伝統的に用いられてきた手法に致命的な問題があることが2016年に分かり、それ以降、この問題はあらためて「現代化学の難題」となり注目を集めていました。
「超分子錯体の会合比の決定」は、弱い相互作用やその化学平衡を理解する上で、最も基本・根本となる課題です。そのため今回の発見は、影響力や波及効果が大きく、医薬品開発や生命科学分野など幅広い分野への影響が及ぶことが想定されます。

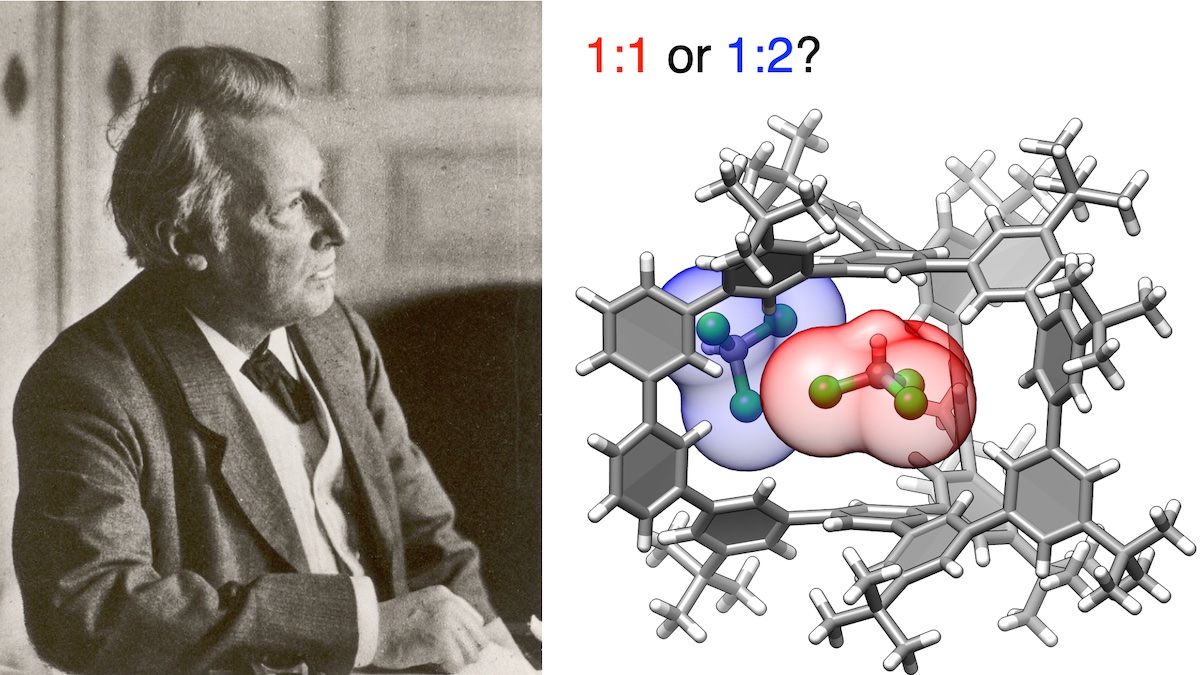
「かご状ホストのなかに、ゲストは何個？」
J. H. ファントホッフ（第1回ノーベル賞受賞者）と今回の研究での超分子錯体

発表概要

東京大学大学院理学系研究科の磯部寛之教授、池本晃喜准教授の研究グループは、超分子錯体の会合比の新しい決定法を発見しました。超分子錯体とは、複数の分子が弱い相互作用を介して会合したものです。超分子錯体の科学を理解することは、生体内反応の理解や医薬品の開発に大いに寄与しています。超分子錯体の理解には、「超分子錯体の会合比を決定すること」が最も大切です。1920年代に解決したと思われていたこの課題は、近年、信頼できる解法がないことが判明し、「現代化学での難題」として再注目されています。本研究では、ファントホッフが1884年に編み出した手法「ファントホッフ・プロット」（第1回ノーベル化学賞）を、この「現代化学での難題」に適用することで、会合比についての明確な解答が得られることを発見しました。新たに合成したかご状分子をホストとした研究を契機に、超分子化学分野での新手法が開拓されました。

発表内容

＜研究前夜＞
1884年、オランダの化学者J.H.ファントホッフは「化学反応速度論に関する研究」という著書を出版し、化学平衡の基礎を創成した。この著書は、平衡定数の概念や化学平衡式の双方向矢印（⇄）を初めて登場させた記念碑的な成果であり、現代科学の基盤を形成した研究として、さらには第１回ノーベル賞（1901）の受賞対象研究として広く認知されている。また、ファントホッフの著書では、温度と平衡定数との関係から熱力学を解析する手法「ファントホッフ・プロット」が初めて登場した。

＜研究内容＞
「複数の分子が弱い相互作用を介して会合する」この現象は、私たちの体内で時々刻々、さまざまな形で進行している化学現象です。この化学現象を理解しようとする分野として、ホスト・ゲスト化学^（^注1）や超分子化学^（注2）が登場してきています。この分野の研究課題は、ノーベル化学賞に複数回（1987年、2016年）取り上げられるなど、現代科学での重要な分野となっています。

複数の分子が弱い相互作用を介して会合した「超分子錯体」の研究では、会合した分子の比（会合比）を決定することが、化学平衡や相互作用を理解するための第一歩であり、最初に決定するべき基盤事項となります。伝統的に会合比の決定には、1928年にフランスの化学者P.ジョブが提案した「ジョブ・プロット」が用いられてきましたが、2016年にその信頼性に疑問があることが明示されたことで、統計学や情報学などを取り込んださまざまな手法が検討・開発され始め、さながら「現代化学での難題」の様相を呈しています。

今回の研究では、ファントホッフが1884年に編み出した手法「ファントホッフ・プロット」（第1回ノーベル化学賞）を、この「現代化学での難題」に適用することで、明確な解答が得られることを発見しました。「ファントホッフ・プロット」は、温度と平衡定数が熱力学により結ばれていることに根ざした解析法で、エントロピー^（注3）やエンタルピー^（注4）という、熱力学パラメータを求めるための方法としてファントホッフが考案したものでした。今回の研究の最大の発見は、「会合比の異なる錯体、それぞれのモデルで、ファントホッフ・プロットを行うと、正しいモデルでは直線関係が確認されるが、誤ったモデルでは直線関係が確認されない」ということです。すなわち、ファントホッフ・プロットが、会合比モデルの判別法として活用できることを見いだしたということになります。

＜具体例紹介＞
具体的な例を一つ紹介します。今回の研究では、フェナインポルクセン^（注5）というかご状分子を設計・合成しています（図1）。研究チームは、まずかごが「ホスト分子」として働き、その中に「ゲスト分子」（クロロホルム）が取り込まれることを見つけました。この超分子錯体では、かごの大きさが十分に大きいため、ホスト・ゲストの会合比が1：1と1：2のいずれでも可能となることが推定されました。そこで、会合比決定法として、F検定法^（注6）や赤池情報量規準^（注7）を用いた会合比決定を試みたところ「1：2」が支持される結果となりました。ところが、この会合比に基づいて解析をさらに進めると、至る所で矛盾が生じることがわかってきました。つまり、「既存の会合比決定法では、どれも誤った会合比が示唆されてしまう」という問題があることが明確になりました。そこで研究チームは、1：1モデルと1：2モデルの双方について、ファントホッフ・プロットを行ってみたところ、「誤った1：2モデルでは直線関係が見いだせない」ということがわかりました。より具体的に言いますと、図1の1：1では、赤い実験値と黒い理論直線が一致していますが、1：2では青い実験値と黒い理論曲線が一致していません。つまり1884年に登場したファントホッフ・プロットが、現代化学の難題となっている「会合比の正しさ・正しくなさ」を判別してくれたということになります。これはまさに「温故知新」がもたらした研究成果です。

＜展望＞
今回の研究で「超分子錯体の会合比の決定」の新しい解法がもたらされたことで、今後さまざまな超分子錯体への適用研究が始まることが期待されます。複数の分子が弱い相互作用を介して会合したものが超分子錯体であり、現代では、その科学を理解することで、生体内反応の理解や医薬品の開発が進められています。今回の研究は、将来、生命科学分野や医薬品開発の現場などで活用される知見をもたらす基盤となることが期待されます。

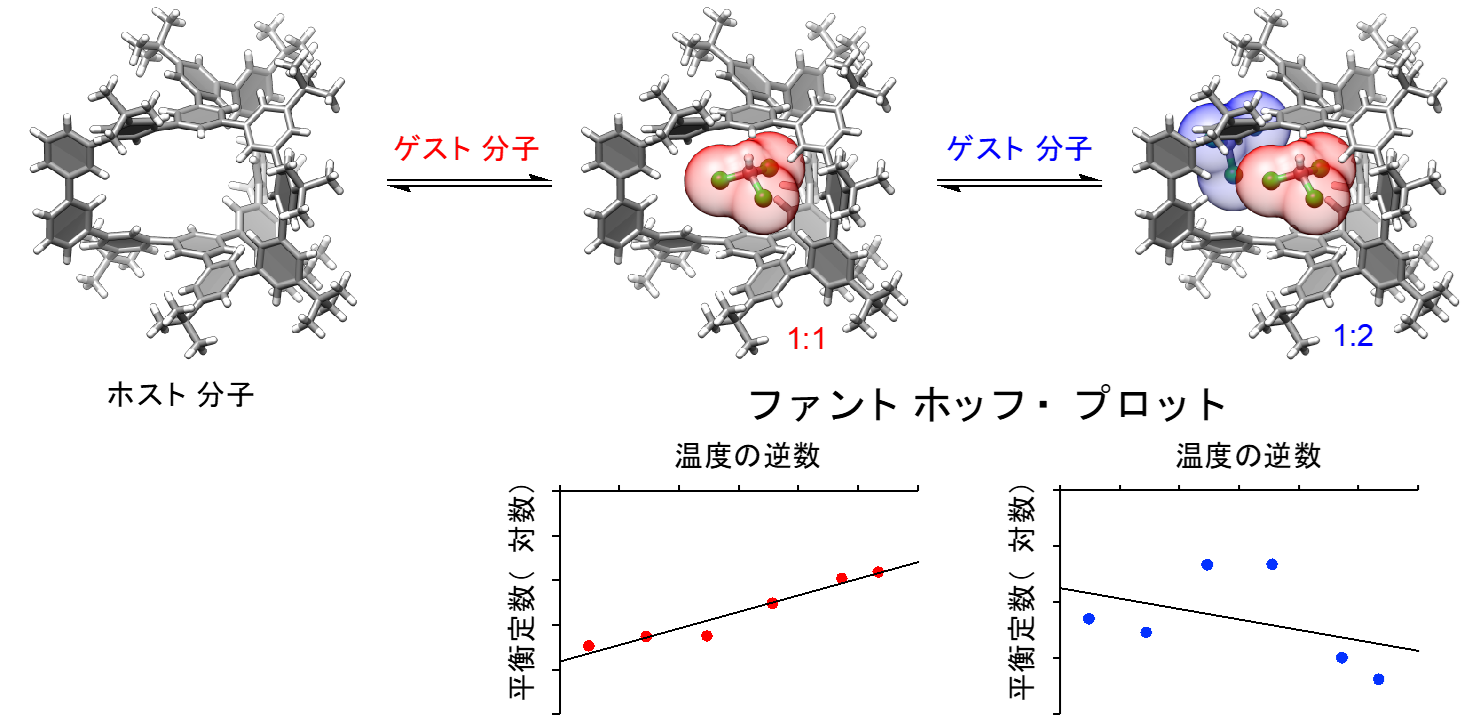
図1：「超分子錯体の会合比の決定」の具体例

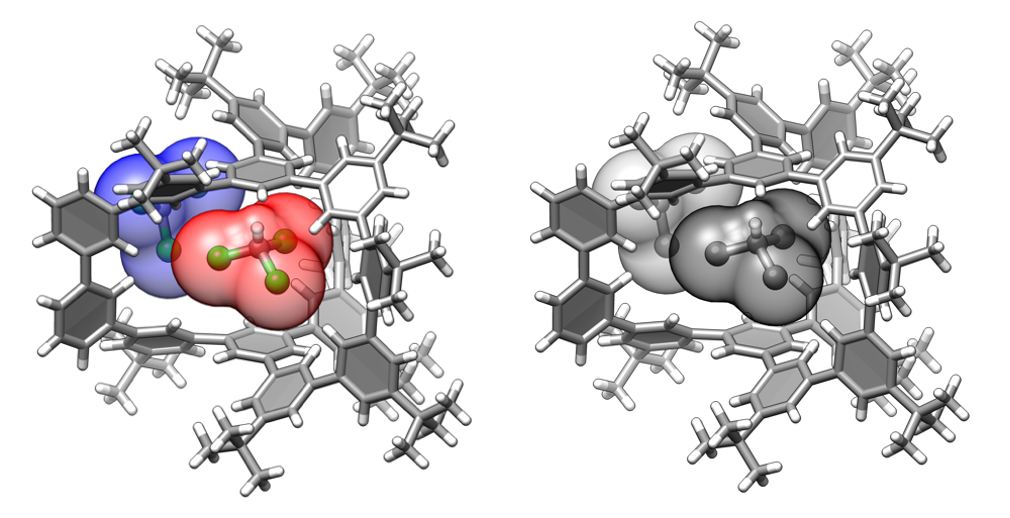
補足図：超分子錯体の分子模型（カラー版と白黒版）

〇関連情報：
磯部寛之教授らの代表的な関連先行研究については、以下のプレスリリースもご参照下さい。

・誕生：ダイアモンドの双子の弟　（2022年2月8日）
https://www.s.u-tokyo.ac.jp/ja/press/2022/7693/
・最小ダイアモンド分子を筒状分子に詰めた分子機械（2021年8月25日）
https://www.s.u-tokyo.ac.jp/ja/press/2021/7511/
・分子で探るモアレの化学 –「不整合炭素二重層」を選んで組み上げ–（2021年3月10日）
https://www.s.u-tokyo.ac.jp/ja/press/2021/7236/
・世界初　窒素ドープ型ナノチューブ分子登場（2020年4月14日）
https://www.s.u-tokyo.ac.jp/ja/press/2020/6741/
・新しいナノチューブ登場（2019年1月11日）
https://warp.da.ndl.go.jp/info:ndljp/pid/12972979/www.s.u-tokyo.ac.jp/ja/press/2019/6191
・研究室の扉：東京大学大学院理学系研究科による動画での研究紹介（2018年11月21日）
https://youtu.be/wdI347pp4OI
・水素結合のリレーで軸回転（2018年9月17日）
https://warp.da.ndl.go.jp/info:ndljp/pid/12972979/www.s.u-tokyo.ac.jp/ja/press/2018/6052
・（ほぼ）摩擦なし：分子の世界のベアリング（2018年5月15日）
https://warp.da.ndl.go.jp/info:ndljp/pid/12972979/www.s.u-tokyo.ac.jp/ja/press/2018/5879
・キラル筒状分子の右手と左手（2017年11月28日）
https://warp.da.ndl.go.jp/info:ndljp/pid/12972979/www.s.u-tokyo.ac.jp/ja/press/2017/5661
・二輪型分子ベアリングの自発的・自己選別組み上げ（2016年11月17日）
https://www.tohoku.ac.jp/japanese/2016/11/press20161117-01.html
・筒状分子の化学と数学（2016年6月28日）
https://www.wpi-aimr.tohoku.ac.jp/jp/achievements/press/2016/20160628_000649.html
・ナフタレンから全固体リチウムイオン電池の負電極材料（2016年5月16日）
https://www.wpi-aimr.tohoku.ac.jp/jp/news/press/2016/20160516_000632.html
・トルエンから単層有機ELの新材料（2015年11月5日）
https://www.wpi-aimr.tohoku.ac.jp/jp/news/press/2015/20151105_000587.html
・ナノサイズのコマの歳差と自転運動（2015年3月2日）
https://www.wpi-aimr.tohoku.ac.jp/jp/news/press/2015/20150302_000541.html
・有限長カーボンナノチューブ分子内部の秘密（2014年5月27日）
https://www.wpi-aimr.tohoku.ac.jp/jp/news/press/2014/20140527_000468.html
・カーボンナノチューブの有限長指標（ものさし）について（2014年1月22日）
https://www.wpi-aimr.tohoku.ac.jp/jp/news/press/2014/20140122_000443.html
https://www.chem.s.u-tokyo.ac.jp/users/physorg/finite/
・顔料から伸長型有限長カーボンナノチューブ分子（2013年5月22日）
https://www.wpi-aimr.tohoku.ac.jp/jp/news/press/2013/20130522_000388.html
・有限長カーボンナノチューブ分子を活用した溶液中のナノベアリングについて（2013年1月9日）
https://www.tohoku.ac.jp/japanese/2013/01/press20130108-01.html
・世界初ジグザグ型有限長カーボンナノチューブ分子の化学合成について（2012年7月18日）
https://www.tohoku.ac.jp/japanese/2012/07/press20120710-01web.html
・世界初らせん型有限長カーボンナノチューブ分子の選択的化学合成について（2011年10月12日）
https://www.tohoku.ac.jp/japanese/2011/10/press20111006-02.html

論文情報

雑誌名 Nature Communications論文タイトル Stoichiometry validation of supramolecular complexes with a hydrocarbon cage host by van’t Hoff analyses 著者 福永隼也、尾仲柚香、加藤昴英、池本晃喜*、磯部寛之* Toshiya M. Fukunaga, Yuzuka Onaka, Takahide Kato, Koki Ikemoto* and Hiroyuki Isobe* DOI番号 10.1038/s41467-023-43979-5

研究助成

本研究は、日本学術振興会科学研究費補助金（課題番号：20H05672、22H02059、22K20527）とJST ACT-X JPMJAX23DIの支援により実施されました。X線回折による分子構造決定には、高エネルギー加速器研究機構(KEK)物質構造科学研究所フォトンファクトリーの最先端設備が活用されています。