ニューラルネットワークが最小限のデータで学習できることを厳密な数学で証明、量子AIに「新たな希望」をもたらし、量子的優位性に向けて大きな一歩を踏み出した Rigorous math proves neural networks can train on minimal data, providing ‘new hope’ for quantum AI and taking a big step toward quantum advantage
2022-08-24 アメリカ・ロスアラモス国立研究所(LANL)
量子AIが、非常に小さなデータセットで訓練した後、相転移をまたいで量子状態を分類できることを示しました。
<関連情報>
少ない学習データからの量子機械学習における汎化 Generalization in quantum machine learning from few training data
Matthias C. Caro,Hsin-Yuan Huang,M. Cerezo,Kunal Sharma,Andrew Sornborger,Lukasz Cincio & Patrick J. Coles
Nature Communications Published:22 August 2022
DOI:https://doi.org/10.1038/s41467-022-32550-3
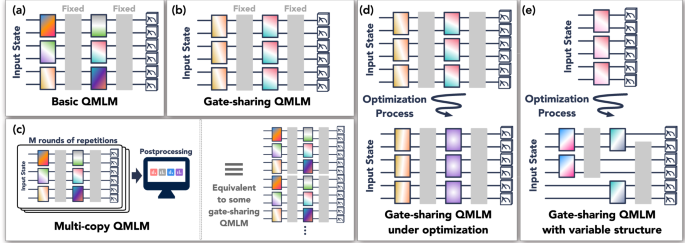
Abstract
Modern quantum machine learning (QML) methods involve variationally optimizing a parameterized quantum circuit on a training data set, and subsequently making predictions on a testing data set (i.e., generalizing). In this work, we provide a comprehensive study of generalization performance in QML after training on a limited number N of training data points. We show that the generalization error of a quantum machine learning model with T trainable gates scales at worst as T/N−−−−√<?XML:NAMESPACE PREFIX = “[default] http://www.w3.org/1998/Math/MathML” NS = “http://www.w3.org/1998/Math/MathML” />T/N. When only K ≪ T gates have undergone substantial change in the optimization process, we prove that the generalization error improves to K/N−−−−√K/N. Our results imply that the compiling of unitaries into a polynomial number of native gates, a crucial application for the quantum computing industry that typically uses exponential-size training data, can be sped up significantly. We also show that classification of quantum states across a phase transition with a quantum convolutional neural network requires only a very small training data set. Other potential applications include learning quantum error correcting codes or quantum dynamical simulation. Our work injects new hope into the field of QML, as good generalization is guaranteed from few training data.