2021-12-22 理化学研究所
理化学研究所(理研)数理創造プログラムの広野雄士客員研究員、岡田崇上級研究員、宮﨑弘安上級研究員、日高義将客員研究員の研究チームは、「ホモロジー代数[1]」という数学の手法を用いて、複雑な化学反応ネットワークを単純化するための新たな縮約手法を開発しました。
本研究成果により、複雑な化学反応ネットワークを、その重要な性質は保ちつつ、より小さなネットワークへと単純化し、効率的に解析することが可能になります。本研究は物理学者、数学者、生物学者から成る研究チームによるもので、分野横断的なアプローチの有効性を示す例となっています。
生体内では数千種類の化学反応が連鎖してネットワークを形成していますが、このような複雑な化学反応系[2]の振る舞いを理解するのは容易ではありません。
今回研究チームが開発した縮約手法は、化学反応ネットワークから部分構造を選び、その部分構造を除去するとともに反応の適切な再結合を行うという過程から成ります。特に、部分構造がある条件を満たす場合には、その部分構造を縮約して得られるより小さなネットワークが元の化学反応系の定常状態[3]を再現することを証明しました。この条件は部分構造の形だけで決まり、反応パラメータの値や反応速度関数[4]の形など反応の詳細には依存しないことから、本手法は幅広い化学反応系に適用できます。
本研究は、科学雑誌『Physical Review Research』(11月17日付)に掲載されました。
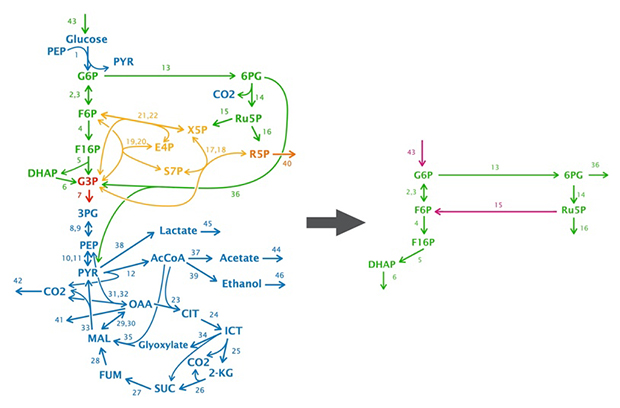
化学反応ネットワーク(大腸菌中心代謝系)の縮約の例
背景
生体内では化学反応が複雑なネットワークを形成しており、そこから生み出される生理機能は生命活動において必要不可欠です。細胞内では数千種類の化学反応が連鎖しており、このような複雑な化学反応系の振る舞いを理解するのは容易ではありません。
特に生体内反応の場合、各反応のパラメータの値や反応速度関数の形を実験的に決定することは困難です。仮に、パラメータと反応速度関数を全て指定し、反応分子濃度の時間変化をシミュレーションできたとしても、モデルが複雑すぎるために重要なパラメータを特定するのは簡単ではありません。また、化学反応系の振る舞いのどの部分が仮定されたパラメータや反応速度関数に依存するのかも分かりません。
そのため、複雑な化学反応ネットワークから重要な部分をいかにして引き出すかが重要な課題となります。化学反応系の縮約はそのための方法の一つですが、既存の縮約手法は反応パラメータや反応速度関数が特定の条件を満たしていないと適用できず、このような情報が得られる場合は限られていました。
研究手法と成果
研究チームは、ネットワークの形だけに基づいた化学反応ネットワークの新たな縮約手法を構築しました(下図上段)。縮約の過程は、(1) 部分構造を選択し、(2) 選んだ部分構造を除去するとともに反応の適切な再結合を行い、より小さな反応ネットワークを作る、というニつのステップから成ります。除去すべき部分構造を選ぶ上で、「影響指数」が重要な役割を果たします。影響指数は部分構造の形から決まるゼロ以上の整数で、以下のように定義されます。
(影響指数)= -(分子種の数)+(反応の数)-(ループ構造の数)
研究チームは、ある部分構造の影響指数がゼロである場合では、その部分構造を除去してできる小さいネットワークが、(残っている変数に関して)元のネットワークと全く同じ定常状態を持つことを数学的に証明しました(下図下段)。従って、影響指数を用いることで、周りに影響を与えることなく除去できる部分構造を同定し、その部分構造を縮約することで化学反応ネットワークを単純化できます。
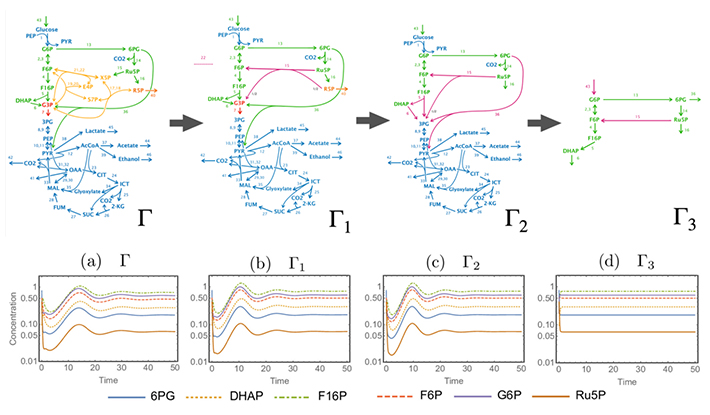
図 化学反応ネットワークの縮約の例と縮約前後の代謝分子濃度の時間発展
上段)大腸菌の中心代謝系の化学反応ネットワーク(Γ)から、部分構造を縮約していったもの。縮約は逐次的に行える。
下段)上段の反応ネットワークにおける代謝分子濃度の時間発展の比較。途中の時間発展には差があっても、最終的に行き着く定常状態の値はどのネットワークで計算しても全く同じになる。これは縮約した部分の影響指数がゼロであることから保証される。
前述のように、既存の縮約手法は、反応パラメータや反応速度関数が特定の条件を満たす場合にしか適用できませんでした。本手法では、部分構造の選択に使われる影響指数は部分構造の形だけで決定され、パラメータの値や反応速度関数の関数形といった系の詳細には依存しません。従って、一般の化学反応系に広く適用することができ、反応の詳細が不明であっても、影響指数がゼロでありさえすれば、他の部分に影響を与えることなくその部分構造を取り除き、化学反応系を簡単化できます。
今回の結果を証明する上で、「ホモロジー代数」という数学の手法を用いました。まず、反応ネットワークに対して定常状態の性質を特徴付けるホモロジー群[1]を定義します。部分構造の縮約の過程は、数学的にはチェイン複体[5]の短完全系列[6]として定式化でき、そこから導かれるホモロジー群の長完全系列から、縮約前と後の反応系の定常状態の関係が規定されます。
今後の期待
今回開発した縮約手法を用いることで、全く同じ定常状態を持つ化学反応系を、より少ない変数で表現できます。すると、大きな反応ネットワークの性質をより小さなネットワークを用いて効率的に調べられます。他に影響を与えることなく縮約可能な部分構造の条件は、部分構造の形のみに依存し、各反応の詳細が不明であっても問題ないことから、この手法は一般の化学反応系に広く適用できます。
また、化学反応ネットワークは通常のグラフを一般化した超グラフ[7]になっており、通常のネットワークは化学反応ネットワークの特殊な場合と見なせるため、本手法は通常のネットワーク上の流れの記述に対しても適用可能です。
ホモロジー代数という数学の手法が化学反応系を解析する上で有用であることを明らかにした本研究成果は、物理学者、数学者、生物学者から成る研究チームによるもので、分野横断的なアプローチの有効性を示す例となっています。
補足説明
1.ホモロジー代数、ホモロジー群
ホモロジー代数は、幾何学的な対象(図形)の本質的な情報を抽出するために用いられる数学の手法。複雑な図形を線型空間と呼ばれる解析しやすい空間に変換して研究できる。この線形空間をホモロジー群と呼ぶ。ホモロジー代数の適用範囲は非常に広く、化学反応ネットワークのような通常の意味では図形と捉えにくい対象にも用いることができる。
2.化学反応系
化学反応が生じる系において、各反応分子の濃度が時間とともにどのように変化していくかを記述する理論的枠組みのことを指す。本研究では、反応分子濃度の変化が決定論的な微分方程式により記述される場合を考えている。
3.定常状態
反応開始から長時間が経過して、系がそれ以上変化しなくなった状態。
4.反応速度関数
ある化学反応が単位時間・体積あたり何回起こるかを、反応分子の濃度の関数として表したもの。
5.チェイン複体
図形を線型空間に変換する際に現れる対象。球面やドーナツの表面といった連続的な図形を、ホモロジー代数を用いて線型空間に変換する際には、図形を三角形の張り合わせに分割する操作が必要となり、チェイン複体はこの分割操作を一般化したものである。この一般化により、化学反応ネットワークのような通常の図形とは異なる対象にも理論を用いることが可能になる。
6.完全系列
ホモロジー代数では図形に対して線型空間を対応させることができるが、図形を変化させたとき、それに応じて線型空間がどのように変化するかを調べることが重要である。完全系列は、この変化の様子を追跡するのに非常に有用な数学的ツール。本研究では、化学反応ネットワークの縮約による変化を追跡する際に完全系列が活躍した。
7.超グラフ
頂点と辺からなるグラフを一般化した概念。グラフの辺が二つの異なる頂点を結ぶのに対し、超グラフの辺は複数の頂点を同時に結べる。複数の分子から複数の分子が生み出される化学反応の連鎖は、数学的には超グラフとして自然に見なすことができる。
研究支援
本研究は、National Research Foundation of Korea (NRF) grant 「Symmetry principles for novel quantum phases (PI: Yuji Hirono)」、日本学術振興会(JSPS)科学研究費補助金研究活動スタート支援「代数多様体のモチーフ理論の一般化に関する研究(研究代表者:宮﨑弘安)」、同新学術領域研究(研究領域提案型)「ブレーンとソリトンの量子異常が導くトポロジカル物質(研究代表者:橋本幸士)」、科学技術振興機構(JST)CREST「作用素論的データ解析に基づく複雑ダイナミクス計算基盤の創出(研究代表者:河原吉伸)」による支援を受けて行われました。
原論文情報
Yuji Hirono, Takashi Okada, Hiroyasu Miyazaki, Yoshimasa Hidaka, “Structural reduction of chemical reaction networks based on topology”, Physical Review Research, 10.1103/PhysRevResearch.3.043123
発表者
理化学研究所
数理創造プログラム
客員研究員 広野 雄士(ひろの ゆうじ)
(Asia Pacific Center for Theoretical Physics, Junior Research Group Leader)
上級研究員 岡田 崇(おかだ たかし)
上級研究員 宮﨑 弘安(みやざき ひろやす)
客員研究員 日高 義将(ひだか よしまさ)
(高エネルギー加速器研究機構 理論センター 教授)
報道担当
理化学研究所 広報室 報道担当