2021-10-21 東京大学
近藤 寛記(物理学専攻 博士課程3年)
赤城 裕(物理学専攻 助教)
発表のポイント
- 量子力学的な波動関数の非自明なトポロジー(注1)に由来して、磁性体中の輸送を担う粒子であるマグノンの特殊な状態が表面に現れるようなモデルを提案した。
- この表面状態は質量をもたないディラック粒子(注2)のような性質を有するほか、運動方向によってマグノンの運ぶスピンの方向が変わるスピン偏極が現れる、電荷を持たないマグノンが電場応答を示すなど、磁性体における新奇物性の宝庫となりえる。
- CrI3などのファンデルワールス磁性体(注3)で上記のマグノンの表面状態が現れることが期待される。
発表概要
原子が周期的に並んだ結晶において、磁性の担い手である電子の自転運動に相当するスピンが規則的に整列する場合、その物質は磁性体と呼ばれます。電子自体が動き回れないような絶縁体でも、このスピンの「動き」が磁性体の性質を支配しています。特に、磁性絶縁体における熱などの伝導現象は、整列した方向からのスピンの傾きが波のように伝わっていくスピン波(図1)によって担われています。

図1:スピン波のイメージ図。上方向にスピンがそろった磁性体において、スピンが上から少し傾いたままずれが波になって伝わるような描像で熱などの伝導現象が記述できる。量子力学において、このような波は同時に粒子とみなすことができ、その粒子がマグノンである。
このスピン波の素励起は量子力学の言葉によって粒子として記述でき、その粒子をマグノンと呼びます。近年、さまざまな対称性の下、マグノンによる非自明な輸送現象に関して研究が盛んに行われていますが、提案された多くの理論模型は現実の物質との結び付きが希薄でした。
東京大学大学院理学系研究科の近藤寛記大学院生および赤城裕助教は、マグノンの波動関数の非自明なトポロジーに由来して、質量をもたないディラック粒子のような分散を持つマグノンが表面に現れる磁性体模型を理論的に提案し、ファンデルワールス磁性体CrI3で実現することを指摘しました。スピンに関する磁気的な対称性だけでなく、結晶の空間的な対称性も組み合わせた対称性により、このトポロジカルマグノン結晶絶縁体が自然に実現します。このような磁性体におけるマグノンは、電場に対して一風変わった応答を示し、新奇物性の宝庫となり得ます。
発表内容
研究の背景
近年、物性物理学の分野では量子物質の研究がますます盛んになっており、とりわけその中で多くの注目を集めているのがトポロジカル絶縁体です。トポロジカル絶縁体とは、物質中の電子の波動関数の非自明なトポロジーに由来して、絶縁体でありながら、その表面/端には「金属」状態が現れる物質のことです。また、この「金属」状態における電子は表面上を一方通行に流れるなどの興味深い性質を示すため、従来の物質では見られなかった多くの現象の舞台となっています。とりわけ、3次元物質で実現した場合は表面(2次元)に「金属」状態が現れますが、自由度が大きいことに由来して、2次元物質における1次元的な端状態よりも多彩な性質を示します。
こうした電子系におけるトポロジカル物性の研究はボース粒子(注4)系へと展開もしており、とりわけ近年研究が盛んなのが、磁性体における基礎的な準粒子(ボース粒子)であるマグノンに関するトポロジカル物性です。その代表例が、温度勾配(と磁場)をかけた方向とは垂直な方向に熱流・温度勾配が生じるというマグノンによるトポロジカル熱ホール効果であり、その理論が提案されてすぐに磁性絶縁体Lu2V2O7で観測されたことで注目を集めました。ここで重要な役割を果たすのが、結晶の空間反転対称性が破れているときに現れる、隣り合うスピンの方向をずらし、ひねりを加えるようなジャロシンスキー・守谷相互作用です。この相互作用があることによってマグノンの波動関数の構造がトポロジーの観点から非自明になり、上記の特殊な表面状態がマグノン系でも現れます。
一方、マグノン系/ボース粒子系は非エルミート性(注5)を内包するため、その特有の数学的性質から理論的展開は自明ではありません。また、昨今のトポロジカル物性に関する研究の爆発的広がりは、時間反転対称性に保護された電子系のトポロジカル絶縁体の提案が発端でしたが、ここで本質的な役割を果たすクラマースの定理(注6)は、直接ボース粒子系には適用できないことから、そのトポロジカル相に関する研究のほとんどは時間反転対称性を持たない系での議論に留まっていました。一歩踏み込んで、マグノン系における有効的な時間反転対称性も導入されましたが、それを3次元系で満たすためには人工的な磁性体のモデルを考えなければなりませんでした。
研究内容
そこで、磁性体における時間反転(スピンの向きの反転)と結晶の単位胞の半分(結晶の周期の半分)の並進操作に関して対称な場合であれば、マグノン系においてもクラマースの定理が適用できることに着目しました。この対称性は、積層構造を持った磁性体において、スピンが互いに反対方向を向きたがるようなスピン間の相互作用の下でそれぞれの層が結びついているときなど、ごく自然な状況下で満たされます。今回の研究では、ハニカム格子が積層した構造を持つ磁性体において、マグノンの特殊な表面状態が現れるような理論模型を提案しました(図2)。

図2:今回提案した磁性体のモデル。ハニカム格子が積層したような構造を持っている。矢印は格子上の原子におけるスピンの方向を表す。ハニカム格子の層内で強磁性的(隣り合うスピンが同じ方向を向こうとする)相互作用が、層の間で反強磁性的(隣り合うスピンが逆の方向を向こうとする)相互作用が働いている場合、スピンは図のような方向に整列する。このような磁性体は、スピンの向きの反転に相当する時間反転と層1つ分の並進を組み合わせた操作に関して対称である。
非自明なトポロジーを有し、結晶の対称性と結びついているため、トポロジカルマグノン結晶絶縁体とも呼ぶべき磁性体です。とりわけ、提案した磁性体のモデルはCrI3などのファンデルワールス磁性体で実現されることが期待されます。そこで実際に、CrI3がモノクリニック構造(単斜晶系)と呼ばれる積層構造を有する場合に、密度汎関数理論(注7)などで推定されたモデルのパラメターに関してこのモデルを調べ、上記の特殊な表面状態が現れていることを明らかにしました。
この表面状態は、質量ゼロのディラック粒子のような線形分散を持っており、運動する方向によってマグノンが運ぶスピンの方向が変わるといった興味深い性質を示します。この性質に由来した新しい物性を引き出すため、電荷を持たないマグノンに対する電場応答を考えました。磁性体に電場をかけることで、結晶内のイオンなどの位置が変更を受け、ジャロシンスキー・守谷相互作用が変化することが知られています。それがマグノンの波動関数にもたらす作用は、アハラノフ・キャッシャー効果(注8)という、電場に由来した複素指数因子の付加とも解釈されます。その寄与を考えたところ、互いに向かい合った磁性体表面におけるマグノンの表面状態のディラック分散がそれぞれ上/下方向にシフトすることを見出しました(図3)。
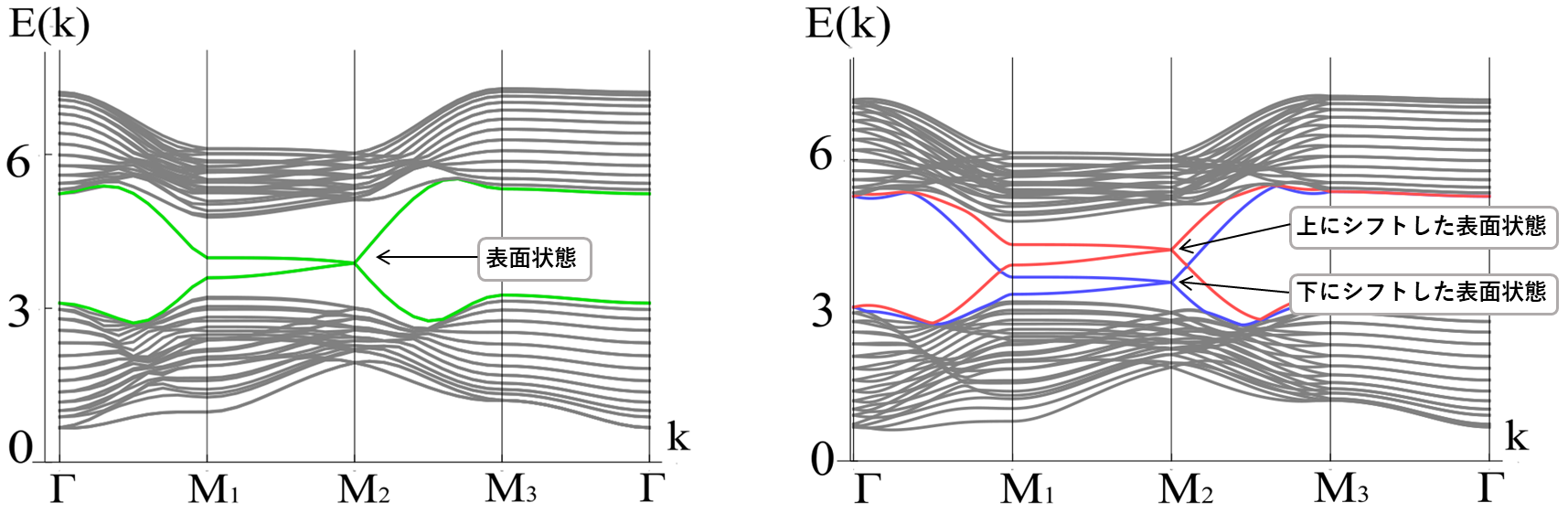
図3:(左)上記の磁性体におけるマグノンのバンド構造(運動量とエネルギーの関係)。束になっている上下2つのバンドをまたいでいる線が表面状態であり、M2点にディラック型の線形分散が現れている。
(右)電場をかけたときのマグノンのバンド構造。電場をかける前は互いに向かい合った2つの表面でバンドが重なっていたが、電場によって一方が上に、他方が下にシフトしている。
このことに起因し、それぞれの表面のマグノン数が増大/減少することで、マグノン流が生じることを明らかにしました(図4)。電荷を持たないマグノンによるこの電場応答は、電子系には対応物のない、質的に新しい輸送現象となっています。

図4:電場をかけたとき、図3でバンド構造が上にシフトした手前側の表面においてマグノン数は増大し、下にシフトしていた奥側の表面で減少する。それに伴ってマグノンは図の方向に流れていく。
今後の展望
本研究で提案された時間反転×並進対称性によって保護されたマグノン状態は、表面に現れるというだけではなく、ディラック型の線形分散を持っている、運動方向に依存したスピン偏極を有する、特殊な電場応答を示すなど、多彩な物性を示します。また、今回考えた電場に関する応答以外にも、多くの新奇物性が潜んでいることが期待されます。本研究提案は、電子が動くことのできない磁性絶縁体におけるマグノンによる新規物性・輸送現象の可能性を切り拓く提案です。今後は、実験的観測・実証に向けた研究展開ならびに、関連した新規物性の探求を考えています。
発表雑誌
- 雑誌名
Physical Review Letters論文タイトル
Dirac surface states in magnonic analogs of topological crystalline insulators著者
Hiroki Kondo* and Yutaka AkagiDOI番号
10.1103/PhysRevLett.127.177201論文URL
Just a moment...
用語解説
注1 トポロジー
連続変形(切ったりくっつけたりはしないような変形)に関して不変であるような幾何学的な性質を調べる数学の一分野。例えば、コーヒーカップとドーナツは同じカタチであることを主張する。
注2 ディラック粒子
相対論的量子力学の枠組みでは、光速に近い速度で運動する粒子はディラック方程式によって記述される。特に、質量を持たないような光子の場合、そのエネルギーは運動量に関して線形になる。グラフェン中の電子など、固体中を流れる粒子が有効的に質量ゼロの粒子として振る舞うことがあり、このような粒子を物性物理分野では一般にディラック粒子と呼んでいる。
注3 ファンデルワールス磁性体
ファンデルワールス力によって、原子の層が積み重なって結合している磁性体。
注4 フェルミ粒子/ボース粒子
自然界に存在する粒子には、量子力学で記述したときの波動関数が粒子の交換によって符号を反転するものとしないものがある。前者をフェルミ粒子、後者をボース粒子という。フェルミ粒子の代表例が電子であり、ボース粒子の代表例が光子やマグノンである。
注5 非エルミート
量子力学における観測量に関わる演算子は一般にエルミート行列として表現される。エルミートとは自分自身と複素転置(エルミート共役)が等しいことである。近年、この枠組を超えた、測定下の量子系や開放量子系などのエルミート性を満たさない、非エルミートな系における物理が盛んに研究されている。
注6 クラマースの定理
相互作用のないフェルミ粒子系(あるいは奇数個のフェルミ粒子からなる系)が時間反転対称性を持っている場合、時間反転によって結びついたエネルギーの縮退した(エネルギーの等しい)状態が存在するという定理。
注7 密度汎関数理論
量子力学における波動関数の代わりに電子密度(による汎関数)を考えることで、相互作用のない場合の方程式に落とし込み、より数値的コストを削減して電子状態を求める方法。物性理論における一大分野を築いている。
注8 アハラノフ・キャッシャー効果
電場中を運動する粒子の波動関数に、その粒子が有する磁気モーメントに依存した複素指数因子がかけられるという効果。よく似たものとして、磁場中の運動に応じて、荷電粒子の波動関数の位相部分が変化するアハラノフ・ボーム効果というものがある。