2019/7/26 アメリカ合衆国カーネギーメロン大学

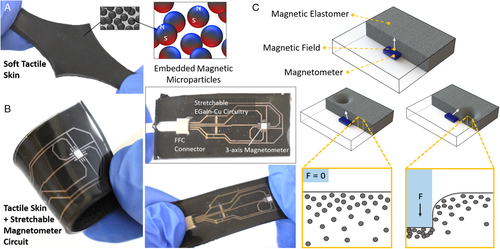
・ カーネギーメロン大学が、単一のタクタイル(触感)センシング素子を備えたソフトなマグネティックスキンを開発。
・ 触感センサーのソフトスキンの多くでは、触感を検知する箇所にワイヤを必要とする。大面積のセンシングではこれらのワイヤが大きな鳥の巣のようになり、複雑化したインターフェースがセンシングシステムの故障を引き起こす可能性がある。
・ 新開発のソフトマグネティックスキンは、ロボット、人間の皮膚や材料等に貼り付けられるストレッチャブルなマグネット状で触感機能を付与する。数百万個の微粒子を充填したシリコーンゴムから構成され、各微粒子の持つ N 極と S 極により発生する磁界を利用して触感を検出する。
・ 同マグネティックスキンが物体に触れるとシリコーンゴムが動きを感知して全微粒子が始動してゴム内部の磁界が変わる。埋め込みマグネトメーターチップがこの磁界の変化を測定し、物体の触れた場所とその強度を推測する。また、磁気を利用するため物体に直接触れない触感検出も可能。
・ 同マグネティックスキンは、バルキーな電子機器や複雑なワイヤリングを使用しないセンシング機能を必要とするロボティック・エンドスコピー(内視鏡検査)において、ブレイクスルーをもたらす可能性が考えられる。
・ 同マグネットスキンのセンサー機能の向上を図るため、内視鏡カテーテルを模倣した筒状の物体に沿った圧力の検出方法とセンシング面積の拡大(現時点では 1.5 ㎠まで)について研究を進める。また、磁性微粒子が作る磁界の拡大やマグネトメーターの配置場所の変更を試みる。
URL: https://engineering.cmu.edu/news-events/news/2019/07/26-majidi-magnetic-skin.html
(関連情報)
Advanced Intelligent Systems 掲載論文(フルテキスト)
Soft Magnetic Skin for Continuous Deformation Sensing
URL: https://onlinelibrary.wiley.com/doi/full/10.1002/aisy.201900025
<NEDO海外技術情報より>
Abstract
Recent progress in soft‐matter sensors has shown improved fabrication techniques, resolution, and range. However, scaling up these sensors into an information‐rich tactile skin remains largely limited by designs that require a corresponding increase in the number of wires to support each new sensing node. To address this, a soft tactile skin that can estimate force and localize contact over a continuous 15 mm2 area with a single integrated circuit and four output wires is introduced. The skin is composed of silicone elastomer loaded with randomly distributed magnetic microparticles. Upon deformation, the magnetic particles change position and orientation with respect to an embedded magnetometer, resulting in a change in the net measured magnetic field. Two experiments are reported to calibrate and estimate both location and force of surface contact. The classification algorithms can localize pressure with an accuracy of >98% on both grid and circle pattern. Regression algorithms can localize pressure to a 3 mm2 area on average. This proof‐of‐concept sensing skin addresses the increasing need for a simple‐to‐fabricate, quick‐to‐integrate, and information‐rich tactile surface for use in robotic manipulation, soft systems, and biomonitoring.