風力発電の出力変動が電力系統へ及ぼす影響の評価手法を開発

大量導入時の安定供給に向け新たな理論

大量導入時の安定供給に向け新たな理論

2018-05-31　科学技術振興機構（ＪＳＴ）　京都大学

ポイント

風力発電の出力はしばしば値が突出し、電力系統に障害を与えることが指摘されているが、外れ値など希少事象の影響を受ける統計量の計算は一般に困難であった。
突発的変動の影響をモンテカルロ法のような標本生成を必要とせず少ない計算量で評価できる確率的なモデリング手法を提案した。
風力発電のみならず、外れ値を伴うさまざまなシステムの解析・設計に向けた新技術の理論基盤として期待される。

ＪＳＴ戦略的創造研究推進事業において、京都大学の加嶋健司　准教授、太田快人　教授らは、風力発電の予測困難な出力変動が電力系統に与える影響を確率的に評価するための理論基盤と実用的計算手法を世界に先駆けて開発しました。

風力発電の出力は、普段は小さな変動幅に留まるものの、突風などにより無視できない頻度で極めて大きな値が発生するという性質があります。この大きく突出した「外れ値」は、電力系統の安定を損なう重要な要因であると指摘されてきました。

本研究では、こうした性質を定量的に評価するための理論基盤を構築し、周波数変動などの統計量を低計算量で計算する実用的手法を開発しました。また、実データに基づく数値実験を行い、提案手法の有効性を実証しました。この技術は、ますます再生可能エネルギーの導入が見込まれる将来の電力システムに対応し、電力の安定供給を実現するための新たな技術として、その発展が期待されます。

本研究成果は、２０１８年５月３０日（米国東部時間）に米国電気電子学会誌「IEEE Transactions on Automatic Control」のオンライン速報版で公開されました。

本成果は、以下の事業・研究領域・研究課題によって得られました。

戦略的創造研究推進事業チーム型研究（ＣＲＥＳＴ）

研究領域：「分散協調型エネルギー管理システム構築のための理論及び基盤技術の創出と融合展開」
（研究総括：藤田政之　東京工業大学　教授）

研究課題名：「太陽光発電予測に基づく調和型電力系統制御のためのシステム理論構築」

研究代表者：井村順一（東京工業大学　教授）

研究期間：平成２７年４月～平成３２年３月

ＪＳＴは本領域で、分散協調型エネルギー管理システムを実現するための研究を電力、制御、経済などの多角的な観点から進めています。本研究課題では、太陽光発電が大量導入された際に、電力系統を安定的に運用するための次世代の電力系統制御技術の構築を目指しています。

その研究展開の１つとして、風力発電が大量導入された電力システムの制御技術にも取り組んでいます。

＜研究の背景と経緯＞

風力発電の電力システムへの導入は、米国や欧州を中心として盛んに進められており、日本でも引き続き導入が進むと見込まれています。しかし導入に際しては、天候などによる出力変動の予測不確実性への対処が非常に重要です。風力発電の出力は、普段は小さな変動幅に留まるものの、突風や乱流の発生などにより無視できない頻度で極めて大きな値が発生するという性質があります。この大きく突出した「外れ値（図１）」は、電力系統に深刻な障害をもたらす一因であることが指摘されてきました。

風力発電の出力変動に対処するためには、「絶対に周波数変動を０．２Ｈｚ以内に納める」といった考え方では実行不可能、もしくは過度に保守的な設計を要求することになります。そこで、「周波数変動は９９．７％以上の割合で０．２Ｈｚ以内に納まる」といった確率的な考え方が欠かせません。

予測困難な性質は一般に、正規分布という扱いやすい性質を仮定することで、統計的に評価します。しかし図１に示すように、正規分布を仮定すると外れ値を評価することができません。これは、風力発電における出力の外れ値が、正規分布で表されるよりも高頻度で発生しているからです。また、正規分布を仮定せずに風力発電の発電変動量の複雑なシミュレーターが構築できたとしても、モンテカルロ法（乱数法）のために大量に外れ値が発生するまで標本の生成を行うことは、必要な標本数の急激な増加により困難であることが知られています。

このような背景から、正規分布のような扱いやすさを持ちながらも外れ値の影響を適切に考慮することができる、新たな理論基盤の構築と、実用的な解析技術の開発が求められていました。

＜研究の内容＞

本研究では、風力発電の出力変動が電力系統へ及ぼす影響を評価するための、確率的評価手法を開発しました。正規分布を拡張した概念である安定分布^注１）を用いて、扱いやすくかつ外れ値を適切に考慮できる新たな確率的なモデル^注２）（電力系統の時間変化を表現する微分方程式）に基づく理論基盤を構築しました。得られたモデルの解析技術として、モデルをシミュレーターとしてデータ標本を生成するのではなく、モデル内のパラメータを用いて直接的にさまざまな統計量を計算する手法も併せて構築しています。この理論基盤は、

１）べき乗則^注３）に従う無視できない頻度で発生する大きな外れ値を扱うことができる。

２）実データからモデルに含まれるパラメータを容易に決定することができる。

３）簡単な計算により、電力系統の各連結点における電圧値、周波数などの変動の統計的性質を特徴づけられる。

という特長を持っています。

この確率的評価手法により、外れ値の発生による電力系統リスク（停電を起こしうる電力系統の不安定状態）を定量的に評価することが可能になりました。

さらに、評価に基づいて対策を打つことで、電力系統の信頼性・経済性の向上に資することが期待できます。本研究では、実際の風力発電における発電変動量のデータから負荷周波数制御^注４）の確率的なモデルを構築し、その統計的性質を提案手法により解析しました。図２は制御に要するコストと平均周波数変動量の関係を表しています。提案手法では、コストが性能改善に寄与する様子が適切に捉えられるのに対して、モンテカルロ法では同様の知見を得にくいことがわかりました。

＜今後の展開＞

本研究で開発した確率的評価手法により、風力発電における出力の外れ値の発生による電力系統リスクを定量的に評価することが可能になりました。さらにそれに基づく対策を打つことで、電力系統の信頼性・経済性の向上に資することが期待できます。

今後は、風力発電の適切な導入量・設備容量の算定や、大規模電源の出力制御などの調整スケジューリングを行う手法として、この評価手法をさらに開発していきます。極めて大きな外れ値の発生可能性も考慮しつつ、より複雑な状況下での電力系統データを用いた検証に発展させ、さらには検証結果を実際の電力システムへ適用することを目指しています。

＜参考図＞

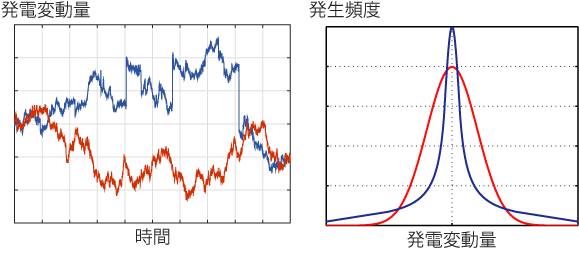
図１　風力発電における外れ値の発生

左）発電変動量（出力の変化の度合い）の時間変化の例。赤線は変動が穏やかな場合。青線は突発的変動がある場合。

右）発電変動量の発生頻度のヒストグラム。

左図の赤線のように、比較的なめらかな時間変動を想定できる場合は、右図の赤線のように正規分布を用いてモデル化することになります。しかし、風力発電における変動量は、ときおり左図の青線のように極めて大きく突発的な変動が発生します。結果として発生頻度のヒストグラムは、右図の青線のように減衰しにくい重い裾をもち、これが外れ値の存在を表しています。

図２　負荷周波数制御に関する数値実験結果

数値実験下で、コストをかけて周波数を制御した結果。縦軸は周波数変動量で、小さい方が望ましい値です。一方、横軸は補助的な経済負荷配分制御^注５）の応答速度を表すパラメータＴであり、Ｔを大きくするほど設置コストが大きくなります。黒線は提案手法、赤線はモンテカルロ法により計算を行った結果を表しています。

提案手法による計算結果は、「Ｔが大きいほど（コストをかけるほど）周波数を安定化できる（黒線が右肩下がりである）」、「しかしコスト効果には限度があり、Ｔを０．００１以上にとる必要性は低い（矢印で示した黒線の屈曲）」といった有益な情報を示唆しています。一方で、モンテカルロ法の計算結果は、提案手法の６００倍程度（提案手法１秒に対してモンテカルロ法１０分）の時間をかけて計算を打ち切った結果にも関わらず、周波数変動量がＴに関して単調減少になっていません。これは、標本数の不足によりモンテカルロ法の計算結果が真の周波数変動値から大きく乖離していることを示しています。

＜用語解説＞

注１）安定分布: 確率分布の一種。通常αで表されるパラメータを有し、α＝２の場合は正規分布となり、２未満の場合はべき乗則に従う重い裾を持つ。頻度分布の裾が指数関数的に減衰する正規分布と比較して、極めて裾の重い分布となり、高い確率で発生する外れ値のモデルとして広く用いられる。
注２）確率的なモデル: 不確実性を持つ特定の現象やシステムの時間変化を記述する数学的な表現。その性質の解析には、乱数を用いて標本を大量に生成して、平均的な挙動を調べるモンテカルロ法が一般的である。提案手法においては、安定分布を用いた確率的な項を有する、時間に関する微分方程式を用いて、電力系統の時間変化を表現している。
注３）べき乗則: 確率分布において、ある値の発生確率が、その絶対値のべき乗に比例すること。
注４）負荷周波数制御: 電力系統の周波数偏差、連系線潮流の変動を検出して制御信号を発電所に伝送し、発電所出力を自動制御することにより、系統周波数を基準値に保持する制御。
注５）経済負荷配分制御: 電力需要の変化に応じて、経済的な出力配分を計算し、発電機出力を調整する制御。一般的には負荷周波数制御よりも長周期の変動の抑制を目的とする。

＜論文情報＞

タイトル：“Stable process approach to analysis of systems under heavy-tailed noise: Modeling and stochastic linearization”
（安定過程による裾の重い雑音下のシステムの解析：モデリングと確率線形化）

doi：10.1109/TAC.2018.2842145