スーパーコンピュータ「富岳」も用いた最先端の計算により実現
2021-08-13 理化学研究所,豊田理化学研究所,早稲田大学
理化学研究所(理研)創発物性科学研究センター計算物質科学研究チームの野村悠祐研究員と豊田理化学研究所/早稲田大学理工学術院総合研究所の今田正俊フェロー/上級研究員・研究院教授の共同研究チームは、機械学習[1]を用いた世界で類を見ない高精度手法により、幾何学的フラストレーションのある量子スピン系[2]の解析を行いました。そして、スピンの向きが絶対零度でも整列せずに、量子力学的に揺らぐ「量子スピン液体[3]」相を発見・確証し、存在領域を特定しました。
本研究成果は、量子スピン液体中でスピンが分裂して生じる「スピノン[4]」の性質を解き明かし、これを量子計算への応用につなげるとともに、現実物質で量子スピン液体を実現するための有用な指針を与えるものと期待できます。
今回、共同研究チームは、機械学習分野で用いられる人工ニューラルネットワーク[1]の一種である制限ボルツマンマシン[5]と物理分野で用いられる強力な関数を組み合わせて、スピン間の高度な量子もつれ[3]を学習させる手法を構築しました。スーパーコンピュータ「富岳」などでこの手法を用いた大規模計算を行い、2次元正方格子上のフラストレーションのある量子スピン模型を世界最高レベルの精度で解析した結果、フラストレーションが強くなる領域において、量子スピン液体相の存在の確証を得ました。さらに、実現した量子スピン液体相の励起構造も調べ、通常のスピンの励起が分裂し、分裂した粒子が独立した粒子のように振る舞う分数化という現象を捉えました。
本研究は、オンライン科学雑誌『Physical Review X』(8月12日付)に掲載されます。
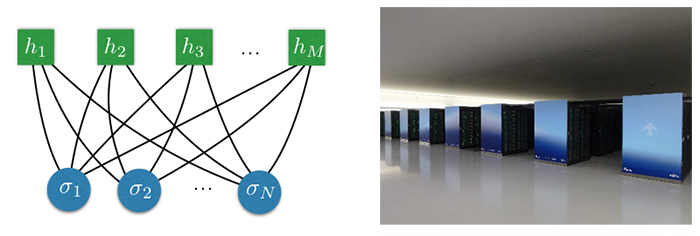
機械学習分野の人工ニューラルネットワーク(左)とスーパーコンピュータ「富岳」の組み合わせにより物理の難問に挑戦した
背景
物質を構成する電子が互いに強く反発し、すみ分けて動けなくなったモット絶縁体などは、電子が持つスピンという量子力学的自由度が互いに相互作用し合う「量子スピン系」と見なせます。通常の場合は相互作用のエネルギーを下げるように、スピンの向きが規則正しく整列する長距離秩序が低温で実現します(スピンの固体)。しかし、互いに異なるスピン配置を好む相互作用が競合し合うような格子構造では、スピンがどう整列するかを決めることができず(幾何学的フラストレーション)、強い量子揺らぎが生じて、絶対零度でもスピンの向きが揺らぐ「量子スピン液体」と呼ばれる状態が実現する可能性があります。
このスピンの固体が”溶けた”液体状態では、通常の磁性体のスピン励起とは異なり、スピンがあたかも分裂したような励起が起こると提案されています。そのような分数化した特殊な励起は「スピノン」と呼ばれ、通常のスピンとは異なる量子もつれの特性を持ち、それが量子コンピュータにおける量子計算に有用と考えられています。
このように、量子スピン液体は基礎物理と応用の両面で重要な量子現象ですが、フラストレーションのある量子スピン模型においては、さまざまなスピン配置のパターンが小さいエネルギースケールで競合し合うために、理論的な取り扱いが難しくなります。そのため、量子スピン液体相が実際に存在するかどうか、また存在した場合にどのような性質のスピン液体なのかは、物理の分野で長年議論されてきたものの、いまだに決着していません。
研究手法と成果
このような物理の難問に挑むためには、世界最高精度でスピン配置間のエネルギー競合を捉えることができる最先端の計算が必須となります。研究チームは、この未踏レベルの計算を達成するために、機械学習技術を用いるという新たなアイデアを導入しました。このアイデアは、膨大なデータからその本質的なパターンを見つけ出すことに長けている機械学習を、量子スピンの膨大なスピン配置パターンの重ね合わせで表現される量子もつれの本質を学習する目的で使おうというものです。
具体的には、機械学習分野で用いられる人工ニューラルネットワークの一種である制限ボルツマンマシンを学習に用いました(図1)。さらに下準備として、物理の分野で使われる関数を用いて、あらかじめ重要な量子もつれを取り込んでおくことで、機械学習の能力をより高度な量子もつれの学習に振り向けるという工夫も凝らしました。
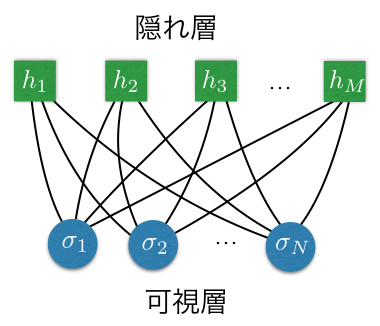
図1 人工ニューラルネットワークの一つである制限ボルツマンマシンの構造の概念図
量子スピン系のスピン配置を、可視層のユニット(青丸)の状態配置に1対1でマップし、その配置間の量子もつれを隠れ層と結合したネットワークによって取り込む。
高度な量子もつれの学習にはさまざまなスピン配置パターンを生成し、そのデータをもとに学習する必要があります。そのような大規模計算を東京大学物性研究所のスーパーコンピュータと理化学研究所のスーパーコンピュータ「京」[6]および「富岳」[7]を用いて行った結果、世界でも類を見ない高精度で量子スピン間のもつれを捉えることに成功しました。
この手法を、2次元正方格子上のJ1-J2量子ハイゼンベルグ模型に適用しました。最近接スピン間の相互作用J1と次近接スピン間の相互作用J2は、それぞれ、ネール型、ストライプ型のスピン配置を好み、競合します(図2)。計算の結果、それらが最も競合する領域(J2/J1 = 0.5付近)において、スピンの液体状態、すなわち、強く量子もつれしている量子スピン液体が実現することが示されました(図3)。
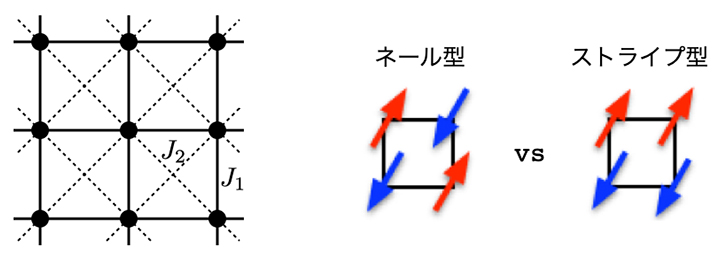
図2 2次元正方格子上のJ1-J2ハイゼンベルグ模型とそのスピン配置の競合
正方形が敷き詰められた格子上の各点に量子スピンが存在し、それらが、最近接スピン間の相互作用J1(実線ボンド)と次近接スピン間の相互作用J2(点線ボンド)によって相互作用し合う。J1とJ2の相互作用(それぞれ正の領域を考える)は、それぞれ、ネール型、ストライプ型のスピン配置を好み、競合する。
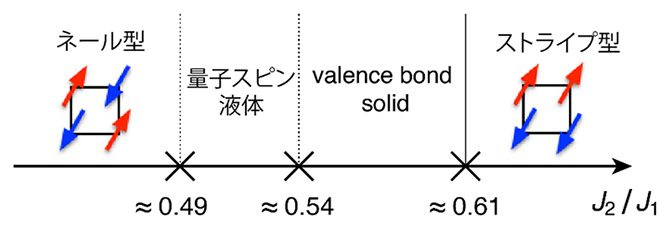
図3 2次元正方格子上のJ1-J2ハイゼンベルグ模型の絶対零度相図
次近接スピン間の相互作用J2が小さければ、最近接スピン間の相互作用J1の影響が支配的になり、ネール型の反強磁性秩序が実現し、J2が大きければJ2の影響が支配的になり、ストライプ型の反強磁性秩序が実現する。それらが競合する領域(J2/J1 = 0.5付近)において、量子スピン液体相とスピンのシングレットが正方格子の対称性を破って整列する共鳴原子価固体(Valence bond solid)と呼ばれる相が実現する。注目すべきは、量子スピン液体状態が幅のあるJ2の領域で実現することである。
異なる相の境界を決めるにあたっては、熱力学的に大きな現実の系の振る舞いを精度よく導き出すために、絶対零度の状態から決める方法と励起状態の構造から決める方法の2種類があり、これらは相補的で同じ物理の表裏の関係にあります。今回、この二つの最先端の相図決定手法が見事に一致した結果を与え、結果の信頼性の確立にさらに貢献しました。
また、その量子スピン液体状態における励起構造を調べたところ、波数空間で対称性の高い一部の波数において、励起エネルギーがゼロになり、その周りでディラック型と呼ばれる円錐状の線形分散を持つスピンの励起構造を持つことが分かりました(図4左)。これは、スピンが分裂してスピノン励起が形成され、それらもディラック型の線形分散を持つという描像とぴったり整合します(図4右)。これらは、量子スピン液体では、分数化した励起が独立した粒子のように振る舞う特別な励起構造を持つことを強く示唆するものです。電子は真空中ではこれ以上分割できない素粒子であると考えられていますが、物質中では分裂して新たな機能を持った粒子による多体現象を生み出すという今回の結果は、物質制御の広大な可能性の一端を示すものです。
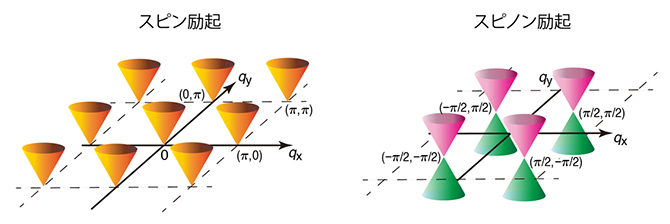
図4 2次元正方格子上のJ1-J2ハイゼンベルグ模型の量子スピン液体相における励起構造
左:計算によって求められたスピンの励起構造の概念図。対称性の高い波数で励起エネルギーがゼロとなりその周りで円錐状に線形分散を持つ。
右:その背後に隠れたスピノン励起の予想される励起エネルギーの構造の概念図。スピノンは独立した粒子のように振る舞うものの、実際の実験では、スピノンを独立に観測することができないため、複数のスピノンの励起によって構成されるスピンの励起(左)が観測される。
今後の期待
今回、量子スピン液体相を示すスピン模型が見つかったことは、量子スピン液体を現実の物質で実現するための有用な指針を与えます。また、量子スピン液体相において発現すると考えられるスピノンというスピンが分裂した特殊な粒子は、量子コンピューティングにおける量子計算への応用が期待できます。
さらに今回の成果は、基礎物理学を発端に、さまざまな学術分野や人類課題への挑戦に使われるようになった機械学習が、今度は物理の難問に挑戦する強力な武器となるという、正のブーメラン効果とでもいうべき波及相乗効果を示しており、物理学の新たな研究フェーズの幕開けとして意義深いものです。機械学習と物理学との親和性の高さが明らかになったことで、今後、学際的な分野融合研究がより活発になるものと期待できます。
補足説明
1.機械学習、人工ニューラルネットワーク
機械学習は、データ間の非自明な関係を非線形関数でモデル化し、データの本質的なパターンを抽出することで、分類や予測などのタスクを行うことを指す。人工ニューラルネットワークは機械学習で用いられる非線形関数の一つで、人間の脳の生体ニューロンを模したユニットから構成される数理モデルである。
2.フラストレーションのある量子スピン系
電子が持つスピンという量子力学的自由度が互いに相互作用し合う系を「量子スピン系」という。量子スピン系は現実物質では、電子が互いに強く反発し合うことで電子が局在化したモット絶縁体などで実現する。「フラストレーション」は、スピンが各格子点に配置されている格子の幾何学的構造や、互いに異なるスピン配置を好む相互作用の競合などによって、全てのスピン相互作用によるエネルギー利得を同時に満たせない状況にあることを指す。例えば、今回考慮した正方格子上での量子スピン模型(図2)においては、J1は正方形の辺で結び付く二つのスピンが反対向き(反強磁性的と呼ぶ)になるとエネルギーが下がるが、J2は対角線で結び付くスピンが反対向きのときにエネルギーが下がる。従って、両者のエネルギーをともに下げることができず、フラストレーション(競合)が生じる。
3.量子スピン液体、量子もつれ
フラストレーションのある量子スピン系においては、さまざまに異なるスピン配置がほぼ同じエネルギーとなるために、絶対零度においても、特定のスピン配置を取らずに、それらのスピン配置が量子力学的に揺らいだ状態が実現する可能性がある。そのような状態を「量子スピン液体」という。量子スピン液体では、遠方にある二つのスピン同士であっても↑↓と↓↑の重ね合わせ(シングレット)のような、無数の配置の量子力学的な重ね合わせ(量子もつれ)になることが重要であり、古典的な状態として表すことができなくなる。この研究は、ポーリングが1933年にベンゼン環の電子状態を2種類の互い違いの二重結合と一重結合の量子力学的重ね合わせ状態として表わしたことにヒントを得て、アンダーソンが1973年にバルクの結晶でも巨視的に無数の状態が重ね合わさった状態が低温で実現する可能性を指摘したことに始まるが、近年になってこの量子もつれを量子計算、量子通信などへ応用する可能性が追究され始め、研究が爆発的に進展し始めている。
4.スピノン
量子スピン液体状態においては、通常の磁性体のスピン励起とは異なり、スピンがあたかも二つに分裂したような励起が発現すると考えられている。スピンが二つに分裂し、それらが、あたかも独立した粒子のように振る舞うとき、その粒子をスピノンと呼ぶ。通常のスピン励起とは異なる量子もつれの特性が量子コンピュータにおける量子計算などに有用と考えられている。
5.制限ボルツマンマシン
人工ニューラルネットワークの一種である確率生成モデル。さまざまな関数形を柔軟に表現できる。統計力学的な確率を発見したボルツマンに因んで、この確率因子(ボルツマン因子)を機械学習の確率に読み替えることで、数理科学、情報科学分野で大きく発展した手法であるが、これがまた物理学の分野に再輸入されてその意義が再認識でされている。
6.スーパーコンピュータ「京」
文部科学省が推進する「革新的ハイパフォーマンス・コンピューティング・インフラ(HPCI)の構築」プログラムの中核システムとして、理研と富士通が共同で開発した計算速度10ペタFLOPS級のスーパーコンピュータ。2012年9月に共用開始。2019年8月にシャットダウン。
7.スーパーコンピュータ「富岳」
スーパーコンピュータ「京」の後継機。2020年代に、社会的・科学的課題の解決で日本の成長に貢献し、世界をリードする成果を生み出すことを目的とし、電力性能、計算性能、ユーザーの利便性・使い勝手の良さ、画期的な成果創出、ビッグデータやAIの加速機能の総合力において世界最高レベルのスーパーコンピュータとして2021年3月に共用開始。
研究支援
本研究は、日本学術振興会(JSPS)科学研究費助成事業基盤研究(S)「強相関物質設計と機能開拓―非平衡系・非周期系への挑戦―(研究代表者:今田正俊)」、同若手研究(B)「強相関物質における格子自由度の役割解明とフォノンがもたらす機能物性の探索(研究代表者:野村悠祐)」、同基盤研究(B)「高次元データの次元圧縮によって実現する磁性と超伝導の第一原理計算(研究代表者:大槻純也)」、文部科学省「富岳」成果創出加速プログラム「量子物質の創発と機能のための基礎科学―「富岳」と最先端実験の密連携による革新的強相関電子科学(研究代表者:今田正俊)(課題番号:hp200132, hp210163)」、ポスト「京」重点課題(7)「次世代の産業を支える新機能デバイス・高性能材料の創成」サブ課題C「超伝導・新機能デバイス材料(研究代表者:今田正俊)(課題番号:hp170263, hp180170, hp190145)」による支援を受けて行われました。
また、本研究には東京大学物性研究所のスーパーコンピュータおよび理研のスーパーコンピュータ「京」、「富岳」が使用されました。
原論文情報
Dirac-type nodal spin liquid revealed by refined quantum many-body solver using neural-network wave function, correlation ratio, and level spectroscopy, “Yusuke Nomura and Masatoshi Imada”, Physical Review X, 10.1103/PhysRevX.11.031034
発表者
理化学研究所
創発物性科学研究センター 計算物質科学研究チーム
研究員 野村 悠祐(のむら ゆうすけ)
豊田理化学研究所
フェロー
早稲田大学 理工学術院総合研究所
上級研究員・研究院教授 今田正俊(いまだ まさとし)
報道担当
理化学研究所 広報室 報道担当
豊田理化学研究所 担当(藤川)
早稲田大学広報室広報課 担当(猪俣)