2022-10-11 東京大学生産技術研究所
○発表者:
田中 肇(研究開始当時:東京大学 生産技術研究所 教授 現在:東京大学名誉教授/東京大学 先端科学技術研究センター シニアプログラムアドバイザー(特任研究員))
黒谷雄司(研究当時:東京大学 大学院工学系研究科 博士課程 現在:豊田中央研究所)
○発表のポイント:
◆アモルファス物質に繰り返し荷重を与えることにより起きる疲労破壊の物理機構を、流体力学の基礎方程式の理論解析・数値シミュレーションにより示した。
◆臨界ひずみ振幅、すなわち元の形状には戻れない変形の始まりは、疲労破壊と単純破壊で同じである可能性を示した。
◆単純変形による破壊の始まりを詳細に調べることで、長時間の疲労破壊試験を行わなくても疲労破壊の臨界ひずみ振幅を予測できる可能性が示され、様々なアモルファス材料の長期安定性の予測に役立つことが期待される。
○発表概要:
疲労破壊は、繰り返し荷重を受けた材料が徐々に局所的かつ構造的な損傷を受け、最終的に破壊に至る現象のことをさします。自動車や航空機に使用される材料を長期間安定に保つために極めて重要です。このような損傷を引き起こす最小のひずみ振幅(臨界ひずみ振幅(注1))は、単純な負荷のもとでの材料が降伏(注2)するひずみよりもはるかに小さいことが知られています。このことから、疲労破壊の閾値は連続荷重下での単純破壊の閾値よりもはるかに小さいと考えられてきました。
田中 肇 東京大学名誉教授(東京大学 先端科学技術研究センター シニアプログラムアドバイザー)と東京大学 大学院工学系研究科の黒谷 雄司 博士課程大学院生(研究当時)らは、アモルファス物質(注3)の疲労破壊現象について、流体力学の基礎方程式と物質の時間的な変化(ダイナミクス)を記述する構成方程式(注4)をもとに、物質の粘弾性的性質(注5)が物質の密度に依存することを考慮し、理論解析と方程式を数値的に解く方法を組み合わせることで、繰り返し単純ずり変形(注6)下での破壊挙動について研究を行ないました。この研究の特徴は、密度、変形(速度)、応力の複雑な結合を考慮し、アモルファス物質の周期的な変形の下での疲労破壊の物理機構を研究した点にあります。この結果、一般に考えられているものとは異なり、臨界ひずみ振幅、すなわち元の形状には戻れない変形(不可逆変形)の始まりは、疲労破壊と単純破壊で同じであることが示されました。これまで、単純破壊において不可逆変形の始まりを正確に測定することは実験上の困難から残念ながら実現されていません。今後その実験的な検出がなされ、この予測が実験的に立証されれば、長時間の疲労破壊実験を行わずとも、一回の単純変形による破壊の臨界ひずみの測定により、疲労破壊の臨界ひずみ振幅を予測できる可能性があり、アモルファス材料設計への応用が期待されます。
本研究成果は、2022年10月11日(英国夏時間10:00am)に「npj Communications Materials」に掲載されました。
○発表内容:
アモルファス材料の降伏・破壊は、高分子のような柔らかい材料からガラスのような硬い材料まで広く観察されます。疲労破壊は、構造物が繰り返し荷重を受けたときに破壊する特異な破壊様式で、与えられるひずみ(または応力)範囲が材料の降伏するひずみよりも遥かに小さくても疲労破壊が起こることが知られています。この特徴から、プラスチックのような材料を比較的弱い力で破壊しようとする場合、日常生活においても、意図的に繰り返し変形を与えることが経験的に行われています。疲労破壊は、材料の長期安定性を支配する、構造物の破壊の中で最も一般的なタイプであり、したがってアモルファス材料の産業応用において重要な意味を持ちます。
この疲労破壊は次のように進行します。まず、繰り返し応力によって微視的な疲労亀裂が発生し、それがサイクルごとに徐々に成長して、最終的に材料の巨視的破壊に至ります。このような疲労破壊は、金属、プラスチック、セラミックス、複合材料など、結晶系、非晶系を問わず様々な材料で普遍的に観察されます。結晶系材料では、既存の欠陥や結晶ドメインの境界(粒界)が疲労破壊の発生に重要な役割を果たすことが広く知られています。一方、そのような欠陥を持たない均一なアモルファス材料では、疲労破壊の発生機構はいまだ解明されていません。最も重要な問題は、なぜ、疲労破壊限界が破壊強度、すなわち、単調荷重に対する降伏応力または破壊応力よりも明らかに小さいかということです。この問題は、様々なアモルファス材料の損傷設計において重要であり、長年その機構が注目されてきました。
この問題を研究するために、本研究グループは、流体力学の基礎方程式と、物質のダイナミクスを記述する構成方程式をもとに、物質の力学的特性の密度依存性を考慮することで、繰り返し変形下での疲労破壊がどのように発生するかについて理論的、数値的に研究しました。一般に、物質の弾性率や外からの刺激に対する応答時間(緩和時間)は密度に依存します。この依存性により一見、体積変化を伴わない単純ずり変形によっても、密度の空間的な変化(揺らぎ)の増大が引き起こされて破壊に至るという機構が本研究グループの過去の研究により示されました[参考文献1、2]。そこでこの機構に基づき、密度、速度、応力場の時間発展を記述する基礎方程式の理論解析により、疲労破壊の臨界ひずみ振幅を推定しました。その結果、密度と粘弾性的性質の結合により、自己触媒的に密度揺らぎが増大し、破壊が発生することを示すとともに、これらの方程式を数値的に解き、シミュレーションにより破壊挙動を明らかにしました(図参照)。
また、疲労破壊には、変形の周期と物質の緩和時間の関係によって、液体型、粘弾性型、弾性型、音響型の4種類の破壊モードがあることを発見しました。液体型は外部から与えられる変形の周波数が物質の応答速度に比べ十分遅いとき、粘弾性型は周波数が物質の応答速度と同程度のとき、弾性型は周波数が物質の応答速度よりも速いとき、音響型は周波数が物質の応答速度よりはるかに速いときに見られる疲労破壊モードです。図は、典型的な弾性型疲労破壊の特徴を示しています。この研究により、アモルファス物質が周期的な単純ずり断変形を受けたとき、どのように、そして、なぜ、破壊するのかについて、簡単な物理的描像を得ることができました。さらに、この理論により、実験的に測定可能なマクロな物理量から、様々な負荷条件に対する臨界ひずみ振幅を予測することが可能になると期待されます。
このような疲労破壊を引き起こす最小のひずみ振幅は、単純な負荷のもとでの材料の降伏ひずみよりもはるかに小さいため、これまで疲労破壊の閾値は連続荷重下での単純破壊の閾値よりもはるかに小さいと考えられてきました。しかし、この常識に反し、本研究により、臨界ひずみ振幅、すなわち、不可逆変形の始まりは、疲労破壊と単純破壊で同じであることが示されました。現状では、単純破壊において不可逆変形が始まる臨界ひずみを実験的に正確に捉えることは困難ですが、この予測が実験的に立証されれば、長時間の疲労破壊実験を行わずとも、一回の単純変形による破壊の臨界ひずみの測定により、疲労破壊の臨界ひずみ振幅を予測できる可能性があり、アモルファス材料設計への応用が期待されます。
本研究は、日本学術振興会特別推進研究(JP20H05619)、基盤研究(A)(JP18H03675)、の支援を受けて実施されました。
参考文献
1.A. Furukawa, H. Tanaka, Violation of the incompressibility of liquid by simple shear flow, Nature 443, 434 (2008)
2.A. Furukawa, H. Tanaka, Inhomogeneous flow and fracture of glassy materials, Nat. Mater. 8, 601 (2009).
○発表雑誌:
雑誌名:「npj Communications Materials」(10月11日)
論文タイトル:Fatigue fracture mechanism of amorphous materials from a density-based coarse-grained model
著者:Yuji Kurotani and Hajime Tanaka
DOI番号:10.1038/s43246-022-00293-9
○問い合わせ先:
東京大学名誉教授
東京大学 先端科学技術研究センター シニアプログラムアドバイザー(特任研究員)
田中 肇(たなか はじめ)
○用語解説:
(注1)ひずみ振幅
材料に繰り返し与えるひずみの振幅。
(注2)降伏
材料を変形すると、ひずみが小さいうちは、応力は歪に応じて線形に増加するが、ひずみが大きくなると不可逆的な変形が始まり、応力の増加率が下がる現象のこと。
(注3)アモルファス物質
原子や分子が結晶状態と異なり規則正しく配列しないで集合している固体物質の総称で、例としては、ゴムやガラス状態の固体などがある。
(注4)構成方程式
物体を構成する物質の外からの作用に対する応答特性を表現する関係式のこと。
(注5)粘弾性的性質
粘弾性とは、弾性体のような伸び縮みする性質と、液体のような流動する性質を兼ね備えた性質のこと。その性質は、物質の硬さ(弾性率)と外部から変形が与えられた時の応答時間(緩和時間)で特徴づけられる。
(注6)単純ずり変形
長方形を高さ一定のもとにずらして平行四辺形に変形するような体積変形を伴わない変形。
○添付資料:
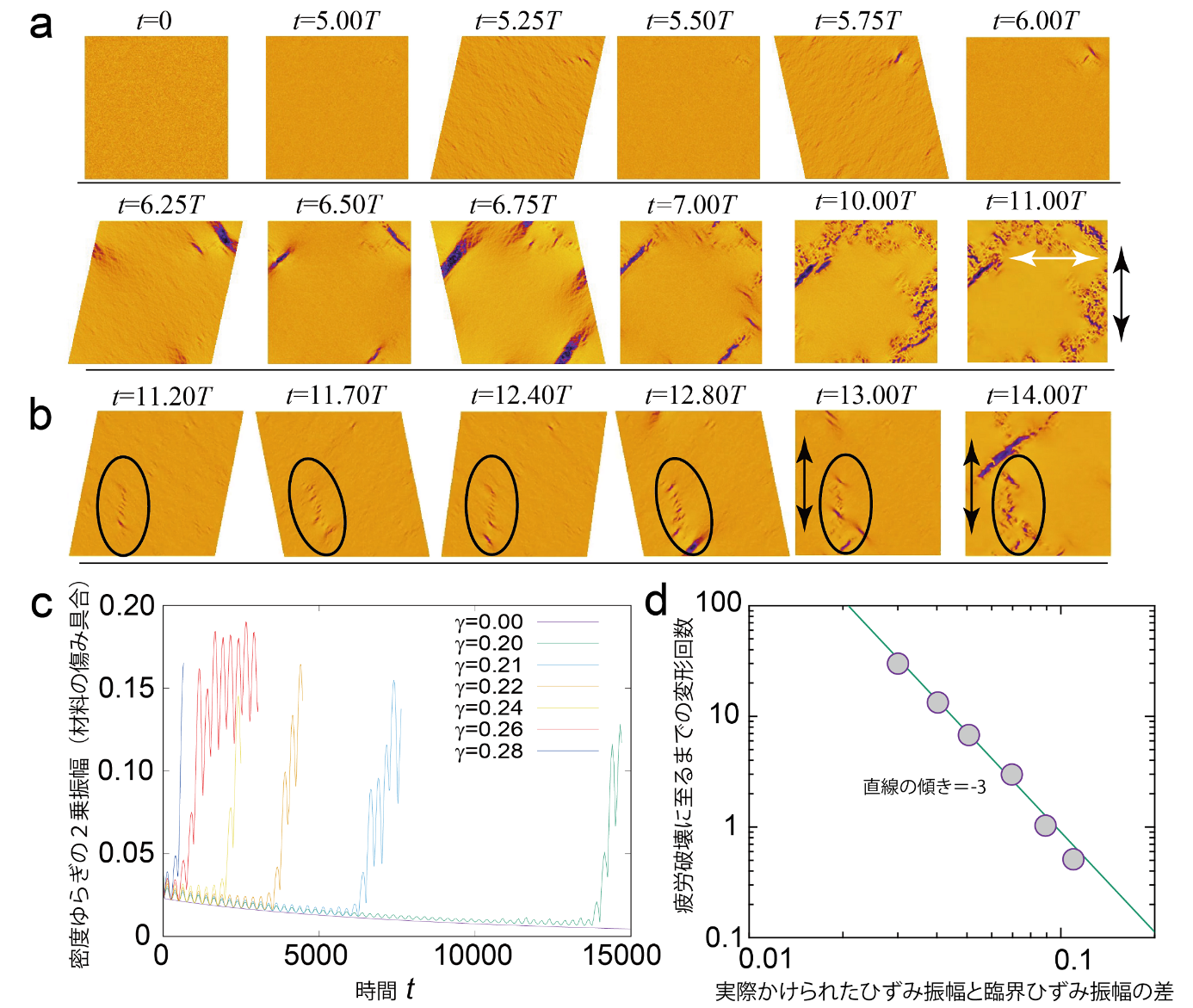
図 弾性型の疲労破壊
(a)弾性型疲労破壊の場合(具体的には、ひずみ振幅γが0.22、変形の周波数ωが物質の緩和周波数の31.1倍の場合)において、密度の揺らぎの時間t(Tは変形の周期)とともに発展し、t=5.25T付近で小さな亀裂が生じ、それがさらに成長し、最終的な破壊にいたる様子(シミュレーション結果)。最初は45°と135°に沿って密度揺らぎと微小な亀裂が発生し、最終的にはそれらが0°と90°の方向に沿って配列することで帯状構造(シアバンド)が形成される(白と黒の矢印を参照)。
(b)弾性型疲労破壊における亀裂の形成過程。微小な亀裂が協同的に配列する様子(丸で囲んだ部分)と、90°に沿った最終的なシアバンド形成に向けた進展が見て取れる。
(c)6種類のひずみ振幅γの値に対して、物質の緩和周波数の31.1倍の変形の周波数ωをもつ振動的なずり変形を与えた場合の密度の揺らぎの2乗振幅の時間依存性。ここで密度揺らぎの振幅は、材料の傷み具合を特徴づける量である。
(d)疲労破壊に至るまでの変形回数の実際に与えられたひずみ振幅γと臨界ひずみ振幅γcの差に対する依存性。この結果から、与えられた変形のひずみの振幅と臨界ひずみ振幅の差が大きいほど、材料が少ない変形回数で疲労破壊することがわかる。さらに、実線は-3の傾きを持ち、変形の振幅と物質が壊れるまでの変形回数に単純な法則性があることがわかる。ここで観察された法則は、実験により得られている経験則を再現している。