量子コンピュータが古典的なコンピュータが不可能とする問題を解決できるようになる瞬間「量子アドバンテージ」は、まだ少し先の話である。 Quantum advantage – the moment when quantum computers can solve problems classical computers find impossible – is still some way off, a study suggests.
2022-05-05 エディンバラ大学
・エジンバラ大学とコペンハーゲン大学の科学者チームは、量子コンピュータの設計とエンジニアリングにおける最近の進展を受け、特定の用途において従来のマシンを凌駕できるかどうかを調査しました。
・最適化問題では、量子アルゴリズムには避けられない不完全性が数多く存在するため、古典的な手法が依然として最高の性能を発揮することがわかった。量子コンピューティングはまだノイズが多すぎる、と専門家は結論づけた。
・現在および次世代の量子コンピュータは、計算誤差(ノイズ率)が大幅に減少しない限り、従来のコンピューティングと比較して特定のタスクを遂行する上で優位性を発揮する可能性は低いことが、研究者らによって明らかにされた。
<関連情報>
- https://www.ed.ac.uk/news/2022/quantum-computing-advantage-as-older-devices-faste
- https://www.nature.com/articles/s41567-021-01356-3
ノイズの多い量子デバイスにおける最適化アルゴリズムの限界 Limitations of optimization algorithms on noisy quantum devices
Daniel Stilck França&Raul García-Patrón
Nature Physics Published: 21 October 2021
DOI:https://doi.org/10.1038/s41567-021-01356-3
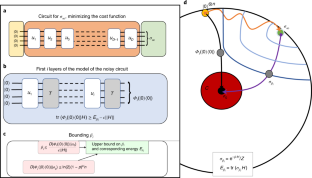
Abstract
Recent successes in producing intermediate-scale quantum devices have focused interest on establishing whether near-term devices could outperform classical computers for practical applications. A central question is whether noise can be overcome in the absence of quantum error correction or if it fundamentally restricts any potential quantum advantage. We present a transparent way of comparing classical and quantum algorithms running on noisy devices for a large family of tasks that includes optimization and variational eigenstate solving. Our approach is based on entropic inequalities that determine how fast the quantum state converges to the fixed point of the noise model, together with established classical methods of Gibbs state simulation. Our techniques are extremely versatile and so may be applied to a large variety of algorithms, noise models and quantum computing architectures. We use our result to provide estimates for problems within reach of current experiments, such as quantum annealers or variational quantum algorithms. The bounds we obtain indicate that substantial quantum advantages are unlikely for classical optimization unless noise rates are decreased by orders of magnitude or the topology of the problem matches that of the device. This is the case even if the number of available qubits increases substantially.