2021-05-25 理化学研究所,カリフォルニア大学,IBM基礎研究所,マサチューセッツ工科大学
理化学研究所(理研)革新知能統合研究センター汎用基盤技術研究グループ数理科学チームの桑原知剛研究員、カリフォルニア大学バークレー校のアヌラーク・アンシュ研究員、IBM基礎研究所(米国)のシュリニバーサン・アルナチャラム研究員、マサチューセッツ工科大学のメーディ・ソレイマニファー大学院生の国際共同研究グループは、量子力学に従う多粒子系(量子多体系[1])を特徴付けるエネルギー関数、すなわちハミルトニアンを少ないサンプルデータ数で効率的に学習する新手法を開発しました。
本研究手法は、今後、未知の量子現象の解明や量子ボルツマンマシン[2]をはじめとした量子機械学習[3]への応用が期待できます。
自然界のあらゆる現象は、「シュレディンガー方程式」と呼ばれる量子力学の基礎方程式を解くことで解明できます。現在、この方程式の構築に必要なハミルトニアンは、量子多体系の観測結果から直接学習できるようになっています。しかし、高精度な「ハミルトニアン学習」に必要なサンプルデータ数は分かっていませんでした。
今回、国際共同研究グループは計算機科学的な手法を用いて、ハミルトニアン学習におけるデータサンプル数の必要十分条件は、量子多体系の粒子数Nに対してNα(1/2 < α < 3)であることを明らかにし、同時に少ないデータ数で効率的にハミルトニアン学習を行う方法を具体的に提案しました。
本研究は、科学雑誌『Nature Physics』オンライン版(5月24日付:日本時間5 月25日)に掲載され、本誌のNews & Viewsで取り上げられました。
Inside quantum black boxes | Nature Physics
背景
量子力学は現代物理学において最も一般的な基礎理論となっており、半導体や超伝導[4]素材の開発や原子レベルで物質を制御するナノテクノロジーの発達など、近代科学の根幹をなしています。この量子力学の基礎方程式が1926年にエルヴィン・シュレディンガーが提案した「シュレディンガー方程式」であり、
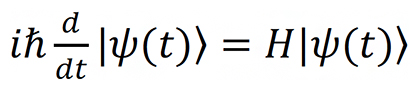
で表されます(ħ:ディラック定数[5]、H:ハミルトニアン、|ψ(t)>:波動関数[6])。自然界の現象は、このシュレディンガー方程式を解くことで原理的に理解することができます。ただし、系のエネルギー関数であるハミルトニアンは対象の量子現象に応じて異なるため、シュレディンガー方程式を解くためには、ハミルトニアンを具体的に決定する必要があります。
どのようにハミルトニアンを決定するのかは、量子力学成立の頃からの重要な問題でした。しかし現在では、量子多体系の観測結果から直接推定することが可能になっており、これを「ハミルトニアン学習」といいます(図1)。ハミルトニアン学習は、量子コンピュータ[7]が正しく動いているかを検証する目的や、量子ボルツマンマシン(量子力学を用いたニューラルネットワークの一種)による機械学習などへの応用も見据えて大きく注目されています。
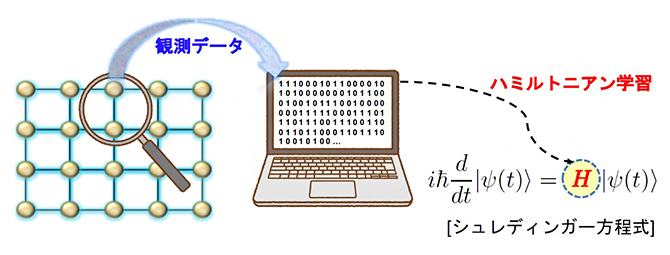
図1 ハミルトニアン学習
近年の量子テクノロジーの進歩により、粒子一つ一つを個別に測定することが可能になっている。このようにして観測で得られた個々の粒子のデータを用いて、ハミルトニアンを学習する。学習して得られたハミルトニアンを用いてシュレディンガー方程式を立て、それを解くことができれば着目する量子多体系の情報は全て得ることができる。
現在までに、ハミルトニアン学習に関してはさまざまな手法が提案されています。しかし、その多くは発見論的・経験論的な手法であり、学習で得られたハミルトニアンが真に正しいのか否かという理論的な保証はありません(ヒューリスティックな方法論)。特に、量子力学ではさまざまな異なる状態の重ね合わせ[8]が許されており、一度の観測のみでは原理的にハミルトニアンを決定できません。それでは、十分に良い精度でハミルトニアン学習を行うためにはどのくらいの数の観測サンプルがあれば良いのでしょうか。これは計算機科学分野では「サンプル複雑性問題」と呼ばれ、長年の未解決問題となっていました。
そこで国際共同研究グループは、ハミルトニアン学習のサンプル複雑性問題を一般的な量子多体系で解決することを目指しました。
研究手法と成果
国際共同研究グループは、「量子ボルツマン分布」を用いたハミルトニアン学習を考えました。量子ボルツマン分布は量子熱平衡状態[9]とも呼ばれ、ある温度の熱浴(一定の温度を保っている十分大きな環境)に接した量子多体系が長時間の後に到達する典型的な状態を指します。量子ボルツマン分布の性質は、温度とハミルトニアンの性質のみで決定されることが知られています。量子ボルツマン分布にある量子多体系はさまざまな状態の重ね合わせになっていますが、観測によって一つの状態への「波束の収縮[10]」が起こります。どの状態へと収縮するかは、確率的に決定されます。このステップを何度も繰り返して、量子ボルツマン分布からハミルトニアン学習を行うためのサンプルデータを得るという方法です(図2)。
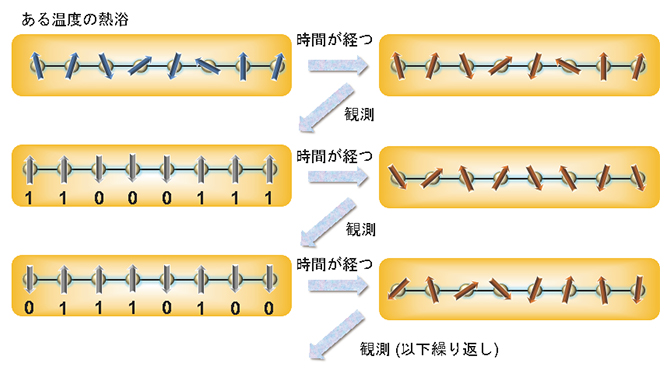
図2 量子ボルツマン分布の観測によるハミルトニアン学習
一定温度の熱浴に接している量子系(上段左側)は、時間が経つと量子ボルツマン分布(上段右側)へと至る。この状態を観測すると波束が収縮し一つのデータが得られる(中段左側)。再び時間が経つと同様の量子ボルツマン分布に至る(中段右側)ので、それを観測すると別の異なるデータが得られる(下段左側)。これを何度も繰り返して、学習のためのサンプルデータを得る。
そして、量子ボルツマン分布の十分統計量[11]が局所的なエネルギーの期待値で与えられることを証明し、ハミルトニアン学習の問題を最大エントロピー法[12]を用いた「最適化問題[13]」の形で表現しました。ここで、局所的なエネルギーの期待値を得るために必要十分なサンプルデータ数は、シャドウ・トモグラフィー[14]と呼ばれる近年の方法論を用いて決定できます。このように定義された最適化問題を解くことでハミルトニアン学習を行います。
学習されたハミルトニアンはサンプルデータ数が有限なために、真のハミルトニアンとの間には統計誤差[15]が生じます。国際共同研究グループは、最適化問題で現れる目的関数に「強い凸性[16]」という性質が成り立てば、学習で得られたハミルトニアンと真のハミルトニアンとの間の誤差を理論的に決定できることを明らかにしました。本研究における最も大きな成果は、量子情報理論、量子多体理論に関するテクニックを駆使して、任意の量子多体系に関して強い凸性を一般的に証明した点にあります。
その結果、ハミルトニアンを精度良く学習するためのデータサンプル数は粒子数Nに対してN3あれば十分であること、データサンプル数がN1/2より少ないと学習は不可能であることが証明できました。これは、ハミルトニアン学習にはNα(1/2 < α < 3)のデータサンプル数が必要十分であることを意味しています。これらの結果から、任意の量子多体系において、ハミルトニアン学習のサンプル複雑性問題を一般に解決することに成功しました。同時に、少ないデータ数で効率的にハミルトニアン学習を行うアルゴリズムを具体的に提案しました。
今後の期待
本研究を通して、量子多体系におけるハミルトニアンを学習するために必要かつ十分なデータサンプル数を一般に解明し、実際に学習する方法論も提示しました。今後、大規模な量子系で実際にハミルトニアン学習を行うには、本研究で構成した計算方法の実行時間を短縮する方法の開発が求められます。
また、必要十分なデータサンプル数Nα(1/2 < α < 3)で指数αを決定し、さらに詳しい最適なデータサンプル数を理解することも重要な課題となっています。これらの理解は今後、量子アルゴリズムや量子計算、量子機械学習などの効率化を目指す上で、重要な知見をもたらすものと期待できます。
補足説明
1.量子多体系
量子力学に従って互いに相互作用する、多数の粒子から構成される系。
2.量子ボルツマンマシン
量子力学を用いたニューラルネットワークの一種。
3.量子機械学習
量子コンピュータを用いて機械学習の問題を効率的に解くこと。一部の問題は量子コンピュータによって超高速化が達成できることが知られている。
4.超伝導
特定の金属を十分に低い温度まで冷やしたときに電気抵抗がゼロになる現象。
5.ディラック定数
プランク定数を円周率の2倍(2π(パイ))で割ったもの。プランク定数は、光子の持つエネルギーと振動数の比例関係を表す比例定数。
6.波動関数
量子力学に従う粒子の状態を記述する複素関数。
7.量子コンピュータ
古典コンピュータの並列計算を、量子もつれの性質などを使って高速に演算処理できるコンピュータ。
8.重ね合わせ
量子力学特有の現象で、0と1のように異なる二つの状態を同時に取ること。
9.量子熱平衡状態
一定の温度を保つ、時間とともに変化しない安定な量子状態。
10.波束の収縮
異なる状態の重ね合わせにある量子状態が、測定によって一つの状態に定まってしまうこと。どの状態に収縮するかは確率的に決定される。
11.十分統計量
ある確率分布を一意に決定するのに必要なパラメータの組のこと。例えば、正規分布では平均値と分散で一意に決まるので、十分統計量は平均値と分散の二つが対応する。
12.最大エントロピー法
データサンプルからもととなる確率分布を決定する際に、取り得る全ての確率分布の中で最もエントロピーが大きい確率分布を得る方法。
13.最適化問題
特定の制約のもとで、ある関数(目的関数)を最大化/最小化する問題。
14.シャドウ・トモグラフィー
複雑な量子状態を断片的な観測結果をもとに推定する方法論を量子トモグラフィーという。シャドウ・トモグラフィーは全体でなく部分系のみに着目し、任意の部分系の状態が観測結果を再現するような量子状態を推定する方法論。
15.統計誤差
ある確率に従って生成されたデータをもとに何らかの統計量を推定するときに、推定された値と真の統計量の間の差のこと。
16.強い凸性
ある多変数関数で、ヘッセ行列(2階の偏導関数が作る正方行列)の最小固有値が0より大きいときに、強い凸性を満たすという。
研究支援
本研究は、日本学術振興会(JSPS)科学研究費補助金若手研究「テンソルネットワーク形式を用いた量子多体問題の計算複雑性解析(研究代表者:桑原知剛)」の支援のもとに行われました。
原論文情報
Anurag Anshu, Srinivasan Arunachalam, Tomotaka Kuwahara, Mehdi Soreimanifar, “Sample-efficient learning of interacting quantum systems”, Nature Physics, 10.1038/s41567-021-01232-0
発表者
理化学研究所
革新知能統合研究センター 汎用基盤技術研究グループ 数理科学チーム
研究員 桑原 知剛(くわはら ともたか)
カリフォルニア大学 バークレー校
研究員 アヌラーク・アンシュ(Anurag Anshu)
IBM基礎研究所(米国)
研究員 シュリニバーサン・アルナチャラム(Srinivasan Arunachalam)
マサチューセッツ工科大学
大学院生 メーディ・ソレイマニファー(Mehdi Soreimanifar)
報道担当
理化学研究所 広報室 報道担当