原子の対称性を超えるナノ物質を発見

次世代電子材料・磁性材料を生み出す新たな指針

2018/09/14 東京工業大学,科学技術振興機構(JST)

ポイント

球対称の原子より高い対称性を持つナノ物質の存在を理論的に証明。
既存物質ではありえないほど、多くのエネルギー状態が重なる。
多く重なったエネルギー状態を利用した次世代の電子・磁性材料の開発に期待。

東京工業大学科学技術創成研究院の春田直毅　特任助教、塚本孝政　特任助教、山元公寿　教授、葛目陽義　特任准教授、神戸徹也　助教らの研究グループは、コンピューターシミュレーションを用いた理論化学的手法^注１）により、特定の金属元素からなる微小な四面体型クラスター^注２）は、既存物質ではありえないほど、多くのエネルギー状態^注３）が重なることを明らかにした。

これらのクラスターは、最も高い対称性^注４）を持ち、最もエネルギー状態が重なるとされてきた原子でも実現できないほどの重なりを示す。この成果は、球対称の原子よりも高い対称性のナノ物質が存在しうることを世界で初めて理論的に証明したものである。こうした重なりを利用すると特異な電気伝導性や磁気特性を引き出すことが可能であり、これまでにない電子材料や磁性材料の開発につながることが期待される。

本研究成果は、２０１８年９月１４日（英国時間）に英科学雑誌「ＮａｔｕｒｅＣｏｍｍｕｎｉｃａｔｉｏｎｓ」オンライン版に掲載される。

本研究は、科学技術振興機構（ＪＳＴ）戦略的創造研究推進事業総括実施型研究（ＥＲＡＴＯ）「山元アトムハイブリッドプロジェクト（山元公寿　研究総括）」で実施された。

＜研究の内容＞

東工大の春田特任助教、塚本特任助教、山元教授らは、コンピューターシミュレーションにより、マグネシウム、亜鉛、カドミウムなどからなる微小な四面体型クラスターは、既存物質ではありえないほど、多くのエネルギー状態が重なることを明らかにした（図１）。縮退^注５）と呼ばれるこうした重なりは、対称性の高い形をした物質ほど起こりやすいとされるが、実現できる縮退度には限界があった（原子より大きな物質では最大でも５重縮退まで）。

今回発見されたクラスターは、そうした幾何学的対称性だけでなく、力学的対称性^注６）と呼ばれる特殊な対称性により、６重縮退や１０重縮退といった超縮退を実現することが分かった。これらの物質は、球対称以上の力学的対称性によって縮退を起こす世界初のナノ物質である。また、本研究では、超縮退を起こすための条件がテオドロスのらせん^注７）に由来する美しい数学的法則で表されることも同時に解明した（図２）。

＜研究の背景と経緯＞

原子は原子核を１個しか持たないため、世界で最も幾何学的対称性の高い球対称の物質と見なされている。そしてその高い対称性により、原子のエネルギー状態は多く重なることが知られている。化学的に安定な希ガス、高い電気伝導性を持つ金属元素、磁石にくっつく磁性元素などの背景には、こうしたエネルギー状態の重なりがある。

原子のように、あるいは原子以上にエネルギー状態が重なるナノ物質があれば、従来にない次世代材料の候補となるが、そういった物質は今まで知られてこなかった。ナノ物質は複数の原子核を持つため、幾何学的対称性が必ず低くなるからである。今回、コンピューターシミュレーションを利用することで、常識に反し、幾何学的対称性とは異なる対称性に基づいてエネルギー状態が重なる超縮退物質を見つけることに成功した。

＜今後の展開＞

超縮退物質の発見はこれまでにない電子材料や磁性材料の開発につながると期待される（図３）。多く重なったエネルギー状態に少しだけキャリア^注８）が混ざれば、高い電気伝導性が引き起こされる。また、多く重なったエネルギー状態に電子が１個ずつ並べば、スピン^注９）が整列し、高い磁性が生み出される。こういったキャリア注入やスピン整列は、四面体型クラスターの構成元素を変えたり、合金化したりすることで実現できる。今後は、こうしたシミュレーション上のナノ物質の実現に向けたクラスター合成に挑むことになる。

＜参考図＞

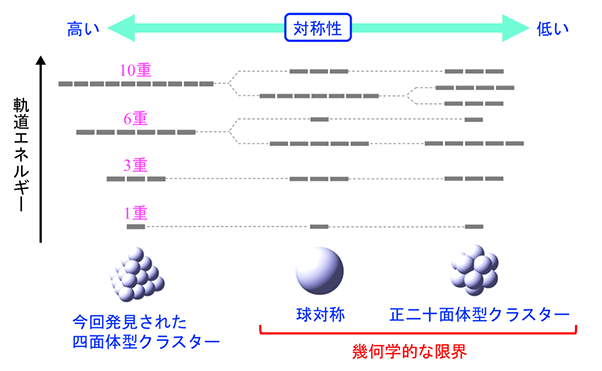
図１

球対称の原子は最も高い幾何学的対称性を持ち、同じエネルギーを持つ状態が最も重なって現れることが知られている。通常、クラスターの対称性は原子の対称性より低いため、原子ほどはエネルギーが重ならない。今回発見された四面体型クラスターは、特異的な対称性を持つことにより、球対称以上の重なりを示すことが明らかとなった。

図２

四面体型クラスターにおいて、各原子間の結合の強さ（トランスファー積分）が、図に示した比になるとき、多くのエネルギー状態が重なることが分かった。ここで現れる平方根の数列√１、√２、√３、√４、⋯は、古代ギリシャのテオドロスによって発見されたものである。

図３

多く重なったエネルギー状態にキャリア注入すると電気伝導体になり、スピン整列させると磁性体になる。

図４

テオドロスのらせん。二辺の長さを１とする直角二等辺三角形の斜辺に、それを底辺とする高さ１の直角三角形をくっつける。さらにその直角三角形の斜辺に、それを底辺とする高さ１の直角三角形をくっつける。これを繰り返すと、大きさの異なる直角三角形がらせん状につながり、各三角形の底辺の長さとして、平方根の数列√１、√２、√３、√４、⋯が現れる。

＜用語解説＞

注１）理論化学的手法: 数学や物理学、コンピューターシミュレーションなどを駆使することで、実験室で実験を行うことなく、物質の性質を明らかにする方法論のこと。実験で得られるデータを精緻に解釈したり、新たな化学現象を予測したりするのに用いられる。
注２）四面体型クラスター: 数個から数十個の原子が集まってできた極小粒子をクラスターと呼ぶ。さまざまな形のものが知られており、四面体型クラスターは４つの三角形の面で囲まれた立体の形をしている。
注３）エネルギー状態: 原子やクラスターは、正電荷を持つ原子核と負電荷を持つ電子の集まりで構成される。各電子は、原子核の周りに広がる軌道に収まる。軌道にはさまざまな形があり、それぞれが異なるエネルギーを持つ。このように軌道は、電子がとりうる各エネルギー状態という意味を持つ。２個の電子までが同じ軌道に入ることができる。
注４）対称性: 物質が持つ形の対称性は、左右対称といった幾何学的な美しさで測られることから、幾何学的対称性と呼ばれる。例えば正多面体は、立体の中でも高い幾何学的対称性を持つ。３次元の世界で、最も高い幾何学的対称性は球の持つ球対称である。
注５）縮退: 原子核が対称に配置されていると、複数の軌道が同じエネルギーを持つことがある。このエネルギー状態の重なりを縮退と呼ぶ。例えば、正二十面体型クラスターでは、５重に縮退した軌道が現れる。通常、クラスターの対称性は原子の球対称より低いため、原子ほどは縮退しない。
注６）力学的対称性: 一般にクラスターの幾何学的対称性は、軌道の形や縮退度に影響を与える。一方で、力学的対称性と呼ばれる非幾何学的対称性も存在する。力学的対称性は、ハミルトニアンと呼ばれる数式を調べることで特定される。今まで原子より大きな物質での例はなかったが、力学的対称性は異常な縮退を引き起こす原因となることが知られている。
注７）テオドロスのらせん: ある一定の規則のもと、大きさの異なる直角三角形をらせん状につなぐと、各三角形の辺の長さとして、平方根の数列√１、√２、√３、√４、⋯が現れる。古代ギリシャの発見者にちなみ、これをテオドロスのらせん（図４）と呼ぶ。超縮退を起こすための条件を書き下すと、この平方根の数列が登場する。
注８）キャリア: 縮退軌道に電子が少しだけ存在すると、近くにあるクラスターの縮退軌道へと電子が移動して電気が流れる。逆に、縮退軌道はほぼ埋まっているが、電子が少し欠けていると、電子の抜け穴（正孔）が動いて電気が流れる。このように電流の担い手となる電子や正孔のことをキャリアと呼ぶ。
注９）スピン: 電子には、スピンと呼ばれる微小な磁石としての性質がある。縮退軌道に電子がちょうど１個ずつ入ると、スピンの向きがそろい、磁性を発現することが知られている。