2023-09-05 スイス連邦工科大学ローザンヌ校(EPFL)
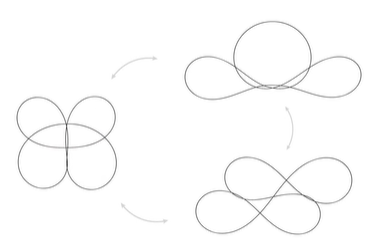
◆この研究は、弾性結び目の幾何学的形状やトポロジカルパターンを明らかにし、新しい構築原則が示され、これらの結び目が新しい構造の設計に活用できる可能性を示唆しています。また、弾性結び目を使用した自己展開構造の設計や、弾性ロッドとファブリック素材の結合など、さまざまな新たな研究方向が探求されています。
<関連情報>
- https://actu.epfl.ch/news/epfl-team-discover-thousands-of-new-transformable-/
- https://dl.acm.org/doi/abs/10.1145/3592399
多安定な弾性結び目の計算による探索 Computational Exploration of Multistable Elastic Knots
Michele Vidulis,Yingying Ren,Julian Panetta,Eitan Grinspun,Mark Pauly
ACM Transactions on Graphics Published:26 July 2023
DOI:https://doi.org/10.1145/3592399
Abstract
We present an algorithmic approach to discover, study, and design multistable elastic knots. Elastic knots are physical realizations of closed curves embedded in 3-space. When endowed with the material thickness and bending resistance of a physical wire, these knots settle into equilibrium states that balance the forces induced by elastic deformation and self-contacts of the wire. In general, elastic knots can have many distinct equilibrium states, i.e. they are multistable mechanical systems. We propose a computational pipeline that combines randomized spatial sampling and physics simulation to efficiently find stable equilibrium states of elastic knots. Leveraging results from knot theory, we run our pipeline on thousands of different topological knot types to create an extensive data set of multistable knots. By applying a series of filters to this data, we discover new transformable knots with interesting geometric and physical properties. A further analysis across knot types reveals geometric and topological patterns, yielding constructive principles that generalize beyond the currently tabulated knot types. We show how multistable elastic knots can be used to design novel deployable structures and engaging recreational puzzles. Several physical prototypes at different scales highlight these applications and validate our simulation.