ピットのエンジニアが、空軍研究所から助成金を受け、量子にヒントを得たアルゴリズムで乱流を正確にシミュレーション。 Pitt engineers receive over 0k from the Air Force Research Laboratory to accurately simulate turbulence through quantum-inspired algorithms
2023-01-03 ピッツバーグ大学
渦と呼ばれる流体の渦のパターンが乱流を作り出し、大小さまざまな渦が空間と時間の中で絶えず変化し、互いに影響し合いながら進化していく。このように複雑なため、従来の計算方法では、正確なシミュレーションに必要な大きな渦と小さな渦の両方を考慮するのに苦労していました。
ピットの研究者は、テンソルネットワーク理論(TNT)に依存したアプローチで、多くの相互作用する物体のいくつかの量子システムの特性を記述する変分波動関数のクラスを包含し、同様の計算複雑さを研究した。
「TNTは、材料科学において極めて重要な広範なモデルを研究するための、確立された計算手法のファミリーです」とメンドーサ・アレナス氏は言います。「TNT は、 量子光学、 量子化学、 高エネルギー、 機械学習などの分野で成功を収め ています。最近では、偏微分方程式を解くために拡張されています。”
特に、スワンソンスクールの機械工学と材料科学の教授であるヘッサム・ババイとペイマン・ギビは、TNTが非圧縮性流体の乱流をうまくシミュレートできることを実証しています。このようなプログラムは、さまざまな種類の乱流力学に関する学術研究だけでなく、自動車、石油、発電、航空宇宙産業にも有益です。
「さらに、圧縮性流体や燃焼化学反応など、より高度な研究が期待されます。「さらに、TNTは量子コンピューティングのプログラミングのための強力なツールであるため、今後の研究により、量子コンピューティングデバイスで乱流をシミュレーションするためのルートを提供することができます。
<関連情報>
- https://news.engineering.pitt.edu/fasten-your-seatbelt—were-experiencing-simulated-turbulence/
- https://www.nature.com/articles/s43588-021-00181-1
乱流構造を利用するための量子的なアプローチ A quantum-inspired approach to exploit turbulence structures
Nikita Gourianov,Michael Lubasch,Sergey Dolgov,Quincy Y. van den Berg,Hessam Babaee,Peyman Givi,Martin Kiffner & Dieter Jaksch
Nature Computational Science Published:13 January 2022
DOI:https://doi.org/10.1038/s43588-021-00181-1
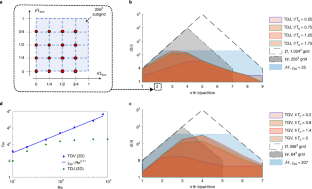
Abstract
Understanding turbulence is key to our comprehension of many natural and technological flow processes. At the heart of this phenomenon lies its intricate multiscale nature, describing the coupling between different-sized eddies in space and time. Here we analyze the structure of turbulent flows by quantifying correlations between different length scales using methods inspired from quantum many-body physics. We present the results for interscale correlations of two paradigmatic flow examples, and use these insights along with tensor network theory to design a structure-resolving algorithm for simulating turbulent flows. With this algorithm, we find that the incompressible Navier–Stokes equations can be accurately solved even when reducing the number of parameters required to represent the velocity field by more than one order of magnitude compared to direct numerical simulation. Our quantum-inspired approach provides a pathway towards conducting computational fluid dynamics on quantum computers.