量子アニーリング計算機のアルゴリズムは、ほとんどの条件下で、量子的な高速化をもたらさないことが新たに証明された Under most conditions, according to a new proof, algorithms on a quantum annealing computer dont offer quantum speedup
2022-08-16 アメリカ・ロスアラモス国立研究所(LANL)
量子コンピューティングは、単純な量子状態を計算結果を持つ状態に変換する。ほんの一握りの量子アルゴリズムでは、この過程が古典的アルゴリズムを凌駕するように調整されている。チューニングされたアルゴリズムは、量子コンピューティングの鍵となる、計算中の異なるシステム履歴の建設的な干渉を保証するために特別に設計されています。
シニツィン氏は言う。「どんな問題でも、無限の時間の間にヒューリスティックに解くことができます。しかし、実際には、計算時間は常に制限されています。研究者たちは、量子効果が、少なくとも、ヒューリスティックなアプローチを実行可能にするために、エラーの数を減らすことを期待しています。」
発見的手法の不確実性に対処するため、シニツィン氏とヤン氏は、量子アニーリング計算機で考えることができるあらゆる計算問題を解決する単純な非同調プロセスを実証する、別の純粋に分析的なアプローチを確立した。この計算の精度は、計算の実行時間のどの時点でも特徴づけることができる。しかし、この精度が古典的アルゴリズムの性能に及ばない場合がほとんどであることを発見した。なぜなら、効率的な量子コンピューティングは、構成的干渉などの量子効果に依存しているからだ。構成的干渉とは、量子プロセッサーが同時に経験する多くの異なる量子履歴が干渉し、最終状態の有用な情報を拡大させることである。しかし、微調整を行わなければ、適切な干渉が起こる可能性は低い。
このように、量子コンピューティングに対する発見的アプローチは、最終的にはうまくいくかもしれませんが、十分な注意を払う必要があります。
<関連情報>
- https://discover.lanl.gov/news/0816-quantum-annealing
- https://www.nature.com/articles/s41467-022-29887-0
任意イジングスピンハミルトニアンに対する非断熱量子アニーリング法の解析的解法 Analytical solution for nonadiabatic quantum annealing to arbitrary Ising spin Hamiltonian
Bin Yan & Nikolai A. Sinitsyn
Nature Communications Published:25 April 2022
DOI:https://doi.org/10.1038/s41467-022-29887-0
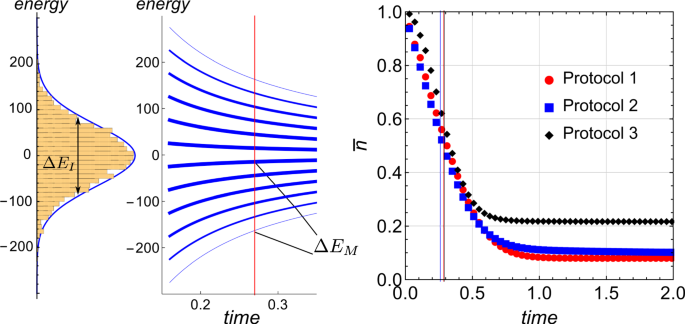
Left: histogram of the spectrum of the Hamiltonian HI(2) with Gaussian distribution of all coefficients a{k}. Middle: time evolution of the spectrum of the transverse field Hamiltonian H0MHM0(17) with quench schedule g(t) = g/t, where g = 4. (Thicker curves correspond to the higher density of states). The vertical line marks the annealing time τa(18), for which the gap between the ground state and the highest density point in the spectrum equals the bandwidth ΔEI (full width at half maximum) of the spectrum of HI. Right: time evolution of the (normalized to 1) excitations n¯≡⟨n⟩/((N−1)/2)n¯≡⟨n⟩/((N−1)/2) for different QA protocols at g = 4 of N = 12 spins. These protocols are tuned to have the same annealing time τa as summarized in Table 1. The colored vertical lines mark the corresponding times at which the excitations reach the halfway into their saturation, which verifies almost the same effective annealing rate for the protocols with the same τa.
Abstract
Ising spin Hamiltonians are often used to encode a computational problem in their ground states. Quantum Annealing (QA) computing searches for such a state by implementing a slow time-dependent evolution from an easy-to-prepare initial state to a low energy state of a target Ising Hamiltonian of quantum spins, HI. Here, we point to the existence of an analytical solution for such a problem for an arbitrary HI beyond the adiabatic limit for QA. This solution provides insights into the accuracy of nonadiabatic computations. Our QA protocol in the pseudo-adiabatic regime leads to a monotonic power-law suppression of nonadiabatic excitations with time T of QA, without any signature of a transition to a glass phase, which is usually characterized by a logarithmic energy relaxation. This behavior suggests that the energy relaxation can differ in classical and quantum spin glasses strongly, when it is assisted by external time-dependent fields. In specific cases of HI, the solution also shows a considerable quantum speedup in computations.



