量子コンピューターでのCO2の振動エネルギー準位の計算

2022-07-14 東京大学

Erik Lötstedt（化学専攻准教授）
山内薫（化学専攻教授）
立川豊（DIC株式会社 QCCプロジェクト・データサイエンスセンター長）

発表のポイント

CO₂分子の振動エネルギー準位を、量子コンピューターibm_kawasakiを用いて計算した。
新しく開発されたハイブリッド固有値アルゴリズム^（注1）と簡単なエラー抑制法を適用することにより、CO₂のフェルミ共鳴振動状態を高精度で計算した。
この結果では、量子コンピューターが多原子分子の振動エネルギー準位の計算に有望であり、量子コンピューターが分子振動の分光研究に役立つものであることを示した。

発表概要

量子コンピューター^（注2）の応用に有望な分野の一つは、原子および分子の量子力学的エネルギー準位の計算である。ただし、現在の量子コンピューターを使用して計算を実行すると、結果にはさまざまなノイズ源に起因するエラーが含まれる。したがって、量子コンピューティングの研究における重要な課題は、ノイズの影響を低減する方法の開発である。

「Qubit による応用量子化学 (AQUABIT)」プロジェクト（https://www.u-tokyo.ac.jp/adm/fsi/ja/projects/quantum/project_00064.htmlを参照）では、エリック・ローツステット准教授、山内薫教授らの研究グループが、DIC株式会社の立川豊のチームとの共同研究を通じて、量子コンピューター上で原子・分子系をシミュレーションするための新しい手法やアルゴリズムを開発している。本研究では、ローツステット、山内、立川が、CO₂分子の振動準位のエネルギー^（注3）を量子コンピューターで正確に計算できることを実証した。

今回、量子コンピューターと古典コンピューター^（注4）の両方を使用し、振動エネルギー準位を計算するための新しいハイブリッド手法を開発した。量子コンピューター上の計算は、新川崎に昨年設置されたIBM製の超伝導型量子コンピューターibm_kawasaki^（注5）を用いた。量子コンピューターで得られたエネルギーを古典的なコンピューターで得られた参照結果と比較することによって、ノイズによる系統的誤差を推定する単純なエラー抑制法を導入し、CO₂のフェルミ共鳴準位^（注6）の準位エネルギーを、0.1 cm^-1（= 0.001 kJ / mol）未満の小さな誤差で計算できることを示した。

本研究により、量子コンピューターが、振動分光学で必要となる多原子分子の正確な振動エネルギー準位を計算するための有望なツールであることが明らかになった。

発表内容

研究の背景
量子コンピューターは、現在のスーパーコンピューターでも扱うことが難しいサイズの大きな分子のエネルギー準位を計算できる可能性があるため、材料科学や応用化学の分野において将来極めて役立つ演算装置となることが期待されている。しかし、現在利用可能な量子コンピューターでは、環境との相互作用から生じる多くの種類のノイズのために量子演算にエラーが生じてしまう。そのため、量子コンピューターで実行された計算結果から、意味のある結果を抽出するためには、ノイズの影響を減らす方法（エラー抑制法）を導入することが必要である。現在、量子コンピューティングの研究は、将来、より大型の量子コンピューターで計算を実行するためのアルゴリズムを開発している段階にあり、現在利用可能な量子コンピューターを用いて、これらのアルゴリズムの検証が行われているところである。今、重要とされていることは、量子コンピューターに必然的に存在するノイズの影響を軽減する有効な方法を開発することである。そして、量子コンピューターを用いた計算では、繰り返し計算を行うことによって、その結果に含まれる統計的エラーと系統的エラーの両方に如何に対応するかが研究対象となっている。

振動分光学では、分子の振動エネルギー準位を実験的に決定すると同時に、分子内のポテンシャルやポテンシャル曲面上での動的な挙動が理論的な手法によって研究されている。一般に、多原子分子のすべての振動準位のエネルギーを計算することは、スーパーコンピューターを用いたとしても、多次元の振動波動関数を扱うために必要となるメモリが大きくなりすぎるため、非常に難しい問題である。そのため、従来の古典コンピューターでは処理できない分子の振動エネルギー準位の計算に、量子コンピューターが役立つことは期待されていたが、既存の量子コンピューターを用いた分子振動エネルギー準位の計算のデモンストレーションは我々の2021年の発表（E. Lötstedt, K. Yamanouchi, T. Tsuchiya, Y. Tachikawa, Phys. Rev. A 103, 062609 (2021)）まで報告例が無かった。

本研究では、量子コンピューターを用いて大きな分子の振動エネルギー準位を効率的に計算するための第一歩として、CO₂分子の振動エネルギー準位を計算した。地球温暖化でよく知られている分子であるCO₂は、フェルミ共鳴が存在するため、振動分光学の観点からも面白い分子である。古典コンピューターと量子コンピューターの両方を使用する縮約多状態短縮変分量子固有値ソルバー（reduced multi-state contracted variational quantum eigensolver, 略してRMC-VQE）法と名付けた新しい手法を提案し、量子コンピューターibm_kawasakiでフェルミ共鳴準位のエネルギーを計算するとともにその波動関数を構築した（図1）。

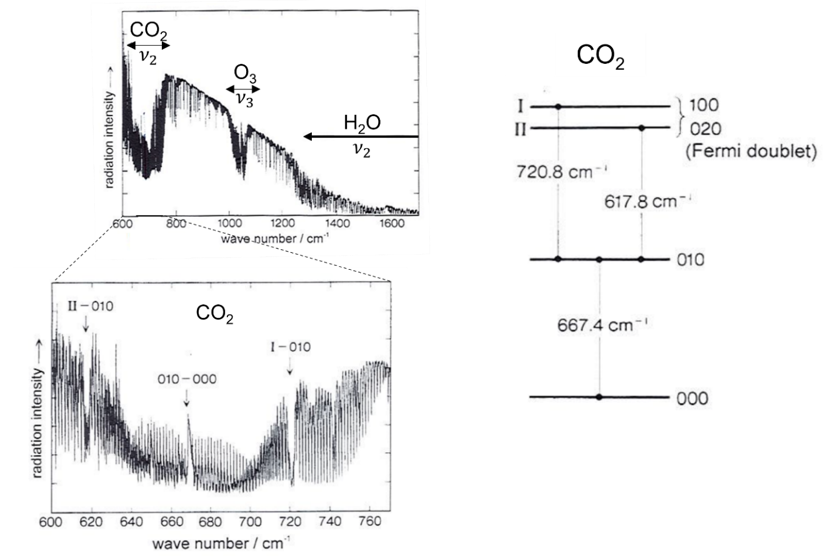
図1：CO₂のフェルミ共鳴の実測と関連するエネルギー準位図
K. Yamanouchi, “Quantum Mechanics of Molecular Structures,” Springer-Verlag, Germany (2012) より転載。

研究内容
RMC-VQE法では、振動波動関数を、「古典」基底関数系と「量子」基底関数系の2種類の基底関数の線形結合で表すことによってハミルトニアン行列^（注7）を計算する。「古典」基底関数系の行列要素は、大きな分子でも古典コンピューターで効率的に計算できるように構成されている。「量子」基底関数系を含む行列要素は、古典コンピューターを計算することは困難であるが、量子コンピューターでは計算は可能である。振動エネルギーは、古典コンピューターでハミルトニアン行列の対角化^（注8）によって得られる。このように、量子コンピューターは、古典コンピューターでは計算することが難しいいくつかの重要な行列要素の計算にのみ使用される。この手法によって、ノイズの影響が軽減されると同時に、古典コンピューターのみを使うよりも正確な振動エネルギー準位の計算が可能となる。

原理実証のため、RMC-VQE法を対称伸縮振動と変角振動を考慮したCO₂の2モードモデルに応用した（図2(a)を参照）。

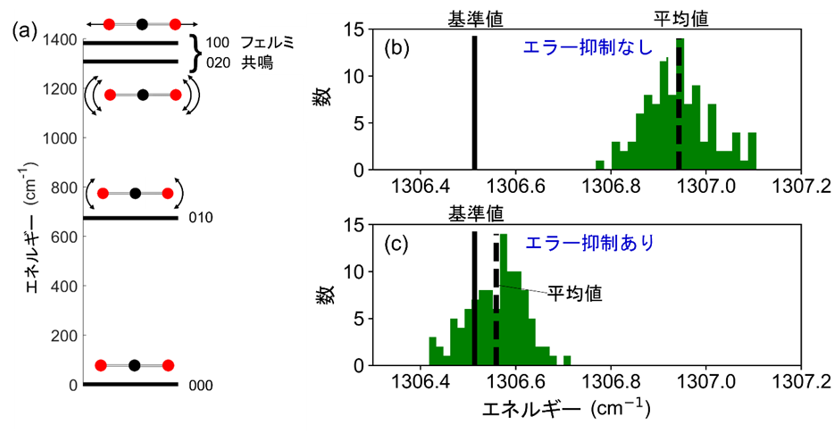
図2： (a) CO₂分子の振動エネルギー準位。(b) ibm_kawasakiで計算されたフェルミ共鳴準位の内の一つの準位についてのエラー抑制無しのエネルギーヒストグラム（緑色）。(c) エラー抑制後のフェルミ共鳴状態のエネルギーヒストグラム（緑色）。

この場合、ハミルトニアン行列は十分に小さいため、正確な参照エネルギー準位を古典コンピューターで計算することができる。このとき、量子コンピューターで計算したエネルギー準位のエラー抑制のため、単純化された基底関数系のハミルトニアン行列を量子コンピューターと古典コンピューターの両方で計算する。量子コンピューターと古典コンピューターで得られるエネルギーを比べることによってエラーを見積もることができる。

量子コンピューターibm_kawasakiで4つの量子ビットを使用して得られた振動エネルギーを図2(b)と(c)に示しす。図2(b)と(c)に示されているエネルギーヒストグラムは、ハミルトニアン行列の計算と対角化を100回繰り返すことで得られた。エラー抑制なし図2(b)では、平均値は正確な基準値と約0.5 cm^-1の誤差はあるが、エラー抑制後図2(c)、平均値は基準値とよく一致している。

社会的意義・今後の予定
CO₂の振動エネルギー準位を正確に計算できることを実証することにより、量子コンピューターが振動分光学に役立つ可能性があることを示した。これからは、より多くの量子ビットを使用して、より大きな多原子分子の振動エネルギーを計算することに取り組んで行く。また、今回新たに導入したRMC-VQE法は、振動エネルギー準位の計算だけでなく、原子や分子の電子エネルギー準位の計算にも適用できる一般的な方法であるため、原子、分子の電子状態計算への応用も期待できる。

発表雑誌

雑誌名 AVS Quantum Science論文タイトル Evaluation of vibrational energies and wave functions of CO₂ on a quantum computer 著者 Erik Lötstedt*, Kaoru Yamanouchi*, and Yutaka Tachikawa DOI番号 Handle Redirect doi.org

用語解説

注1 アルゴリズム
ある特定の問題を解く手順を、単純な計算や操作の組み合わせとして明確に定義したもの。

注2 量子コンピューター
量子ビットから構築されているコンピューター。ビットの値が0か1だけをとる古典コンピューターとは異なり、量子ビットは0と1の重ね合わせ状態をとることができる。量子ビット状態の重ね合わせを利用することで、従来の古典コンピューターよりもはるかに大きな分子のシミュレーションが可能になることが期待されている。

注3 振動準位のエネルギー
分子振動は、量子力学によって記述されるため、振動運動のエネルギーは離散値しかとることができない。その準位を振動エネルギー準位と呼び、そのエネルギーを振動準位のエネルギーと呼ぶ。なお、振動分光学の分野では、分子の振動エネルギー準位を実験的に決定するとともに、分子内のポテンシャルやポテンシャル曲面上での動的な挙動を理論的な手法によって求める。

注4 古典コンピューター
PC、スーパーコンピューター、スマートフォンなどの従来から存在するコンピューター。

注5 ibm_kawasaki
IBM社による27量子ビット量子コンピューター「IBM Quantum System One」。量子ビットは、マイクロ波パルスによって制御される超伝導電子回路でできている。ibm_kawasakiは2021年に新川崎にある「創造のもりかわさき新産業創造センター」に設置された。

注6 フェルミ共鳴準位
103 cm^-1の間隔を持つCO₂の二つの振動エネルギー準位。この小さな分裂は、1931年にEnrico Fermi（エンリコ・フェルミ）によって対称伸縮振動モードの単一励起状態と変角振動モードの二重励起状態が混合した結果生成したものと説明された。

注7 ハミルトニアン行列
量子力学系のエネルギー準位に関する情報を含む行列。準位エネルギーは、ハミルトニアン行列の対角化（^（注8）参照）によって得られる。

注8 対角化
行列の固有値を取得する数値手順。行列の適切な相似変換の後、行列は対角行列要素として固有値を持つ対角行列になる。