量子コンピュータの小型化・高速化を実現する回路圧縮手法を開発

2020-11-12

ソフトウエア新技術で大規模量子コンピュータ開発を加速化

ソフトウエア新技術で大規模量子コンピュータ開発を加速化

2020-11-12 国立情報学研究所

大学共同利用機関法人情報・システム研究機構国立情報学研究所（所長：喜連川優、東京都千代田区、以下NII）と日本電信電話株式会社（本社：東京都千代田区、代表取締役社長：澤田純、以下　NTT）は、大規模な量子コンピュータ上の計算回路の圧縮化とコンパイラ設計のための新しいアプローチを定式化しました。本手法を用いることで、量子計算サブルーチン回路を平均約70％圧縮することが可能となり、大規模量子コンピュータの開発に必要とされるリソースの低減化を実現しました。大規模量子コンピュータに必要とされる量子ビット数の大幅な削減と、計算時間の短縮化による量子コンピュータの高速化が期待されます。

本研究成果は、Phys. Rev. Xに米国東部時間11月11日に掲載されました。

将来開発が期待される大規模な量子コンピュータは、ユーザが量子コンピュータに入力する量子アルゴリズムから、量子コンピュータ内のハードウエア動作までの間に、コンパイルと最適化が何段階にもわたって行われると考えられています。また、このような大規模な量子コンピュータは誤り耐性型汎用量子コンピュータとも呼ばれ、誤りに耐性をもつ符号化の構造をもつことを特徴としており、誤りに耐性をもつ符号へのコンパイルや最適化の手法の開発が、大きな課題のひとつとなっていました。この誤り耐性のある符号化のうち、量子コンピュータの設計にもっとも多用されているのはトポロジカル符号で、中でも特に代表的なのは、超伝導量子ビット実装の２次元表面符号と、主に分散型の量子コンピュータの設計に用いられる３次元トロポジカル符号です。本研究では、これらのトポロジカル符号を統合化し、量子計算回路における最適化を通して、量子コンピュータの誤り耐性実装に伴う大規模なオーバヘッドの低減と、コンパイラ設計の中心となる量子コンピュータ言語への新しいアプローチを提案しました。

背景

最近インターネット経由でも使われ始めている量子コンピュータは、量子コンピュータ中のデータにエラーがあることからNISQ(Noisy Intermediate-Scale Quantum)マシンとも呼ばれ、エラーの影響が大きいことが特徴です。実用上量子優位性を十分に発揮するには、量子ビット操作上のエラーに対して耐性をもつ、大規模量子コンピュータの出現が待たれています。大規模量子コンピュータの最も大きな特徴は、量子誤り訂正を用いて量子計算が誤りに対して耐性をもつように実装されていることです。ところが、誤り耐性をもつように量子誤り訂正符号を実装するためには、非常に多くの量子ビットが必要となり、現在のNISQマシンが100量子ビット以下であるのに対し、100万程度の量子ビットが必要とされると見積もられていることから、開発上の大きな壁となっています。

このような量子誤り訂正符号では、冗長性を利用して数多くの物理量子ビットを用いて論理量子ビットの情報を守ります。その論理量子ビット上の演算は論理ゲート^（*1）の列、すなわち量子計算回路で表されますが、この論理ゲートの種類は用いる誤り訂正符号によって決まります。超伝導量子ビットを用いた量子コンピュータの設計に用いられている２次元表面符号は、格子つなぎ換え（lattice-surgery）を行うのが特徴です。一方、分散性のある大規模量子コンピュータで特に優れている３次元トポロジカル符号は、論理量子ビット同士がつくるトポロジーを変えることで演算を実装します。

２次元表面符号と３次元トポロジカル符号は誤り訂正符号としては同じ仲間に属しますが、その表現も論理ゲートの性質も異なるため、これまで別々に研究が進められてきました。また３次元トポロジカル符号は、圧縮方法の効率化や圧縮後の量子計算回路の検証などの課題も多く、研究は発展途上にあります。

本研究成果

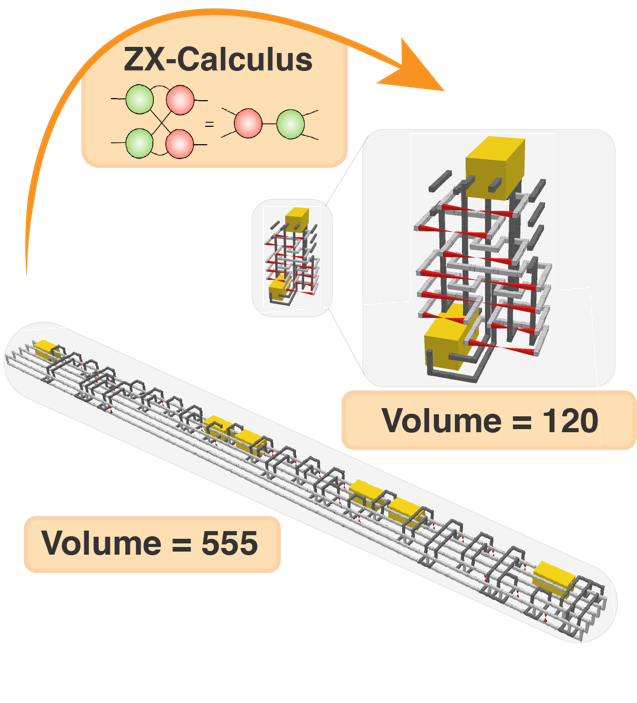
本研究では、まず、ZXカリキュラス^（*2）を３次元トポロジカル符号上の量子計算回路に応用し、ZXカリキュラスのもつ演算機能を用いて量子計算回路の圧縮化を行いました。3次元トポロジカル符号では、論理量子ビットを定義するために挿入されたディフェクトと呼ばれる構造が絡み合うことでトポロジーを変え、演算を実装するために、量子計算回路を絡み合うパイプ構造として３次元的に視覚化することができます（図１参照）。このパイプ構造がつくる体積を圧縮することにより、量子計算回路の圧縮化が達成されます。本研究では、よく使われる量子回路のサブルーチンに対して本手法を用いることにより、平均で約70％の圧縮率を達成することに成功しました。量子計算回路を圧縮した分、量子コンピュータに必要とされる量子ビット数を削減できるだけでなく、量子計算回路の実行時間を短縮化できるため、量子計算を高速化できます。

図１　16量子ビットをインプットとした3次元トポロジカル符号上の量子計算回路の例を示す。計算は左から右へと進む。

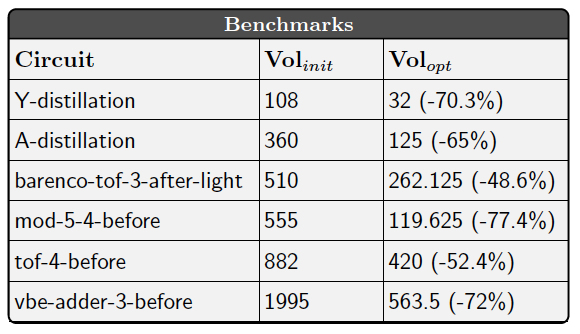
表１　よく用いられる量子計算回路のサブルーチンに対する圧縮率を示す。

本研究ではまた、ZXカリキュラスと3次元トポロジカル符号間の関係性を明らかにすることにも成功しました。つまり、ZXカリキュラスに注目することにより、これまで別に発展してきた2次元表面符号と3次元トポロジカル符号の統一的な扱いを実現し、ZXカリキュラスの量子コンピュータ言語としての可能性を示しました。さらに２つの符号のハイブリッドも可能であることから、従来方法に比べてより高効率な量子計算回路の圧縮を実現できます。また、本手法は複数の量子誤り訂正符号間の行き来を自由に行えるプラットフォームとしても使えることから、将来の大規模量子コンピュータにおける論理量子ビットとハードウエア間の技術層で、コンパイラの設計に有用な量子コンピュータ言語の基礎としての役割を担える点も重要であり、応用面で画期的な道をひらくことが期待されます。

研究の詳細

これまでの3次元トポロジカル符号上の量子計算回路の圧縮は、パイプ構造の変形法則が不完全であることから、圧縮過程で量子計算回路まで変えてしまうなどの様々な問題を含んでいました。これらの問題から、2次元表面符号の方が量子計算回路の圧縮に適しており、優れた性質をもつとの考えが定説となっていました。

本研究ではまず、3次元トポロジカル符号上の量子計算回路の圧縮が回路の性質を変えてしまう問題を回避するため、論理ゲートの変形法則が定式化されているZXカリキュラスに注目し、ZXカリキュラス上で回路の圧縮を行うことにしました。ところが、ZXカリキュラスと3次元トポロジカル符号上の量子計算回路表現（パイプ構造）の間の関係性が解明されていなかったため、この関係性を明らかにし定式化する必要がありました。本研究では、ノードのテンソルネットワークとして表現されるZXカリキュラスに、従来とは異なる新しい解釈を導入することで、3次元トポロジカル符号上のパイプ構造との間に新しい関係性が成り立つことを初めて発見することに成功しました（図２参照）。

ZXカリキュラスを中心に、二次元表面符号と3次元トポロジカル符号の量子計算回路を統合することで、従来の定説を覆し、3次元トポロジカル符号での高い回路圧縮が可能であること、また２つの符号化をハイブリッドしたより効率的な圧縮方法が可能であることを示しました。具体的な例として、多用される量子計算サブルーチンの圧縮に本手法を用いて、従来方法での圧縮回路よりさらに圧縮度の高い量子計算回路を得ることで、手法の有用性を示しました。圧縮後の量子計算回路は、ZXカリキュラスと3次元トポロジカル符号上の量子計算回路表現間の関係をコンパイルに用いて、ハードウエアに回路実装することができます。

図２　3次元トポロジカル符号上の量子計算回路の最適化をZXカリキュラスを用いて行う様子を示す。

将来的な展望

量子コンピュータに実装される量子ビットの数は年々増えていますが、量子コンピュータの本格実用化には、エラーの克服が最重要課題となっており、世界的に誤り耐性を特徴とする大規模量子コンピュータの登場が期待されています。本手法を用いて誤り耐性の実装に必要とされるリソース負荷を低減することにより、より早い大規模量子コンピュータの実現が期待できます。３次元トポロジカル符号に基づく大規模量子コンピュータの制御性の改善とリソースの低減を大幅に進めることができたことは、分散性のあるネットワーク的な量子コンピュータの可能性を飛躍的に高めるものでもあり、NTTが進めるIOWN (Innovative Optical and Wireless Network)構想^（*3）の実現に向けて量子技術からのアプローチを加速するものです。

また、大規模量子コンピュータを設計する上で、本手法は量子コンピュータアーキテクチャと合わせて中心的な位置を占め、命令制御アーキテクチャやコンパイラの設計の基礎としての役割を担っていくことが期待されます。

研究プロジェクトについて

本研究成果は、文部科学省量子飛躍フラッグシッププログラム（Q-LEAP）JPMXS0118069605の支援を受けています。

論文タイトルと著者

タイトル：Effective compression of quantum braided circuits aided by ZX-Calculus
著者：M. R. Hanks, M. P. Estarellas, W. J. Munro, and K. Nemoto
掲載：Physical Review X (2020)
発表日：2020年11月11日（米国東部時間）