線形光円錐問題の数学的な解決～量子力学系での情報伝達に関する原理的限界を解明～

2020-07-13 理化学研究所,慶應義塾大学

理化学研究所（理研）革新知能統合研究センター汎用基盤技術研究グループ数理科学チームの桑原知剛研究員と慶應義塾大学理工学部物理学科の齊藤圭司教授の共同研究チームは、量子力学的な多数の粒子系（量子多体系^[1]）の情報伝達における新たな物理法則を発見しました。

本研究成果は、量子力学的に力が働き合う多数の粒子が示すダイナミクスに新たな知見を与えるだけでなく、量子コンピュータ^[2]など情報処理技術における基本的制約の理解にも貢献すると期待できます。

量子多体系において長距離で働く力は、どんなに遠く離れた粒子間でも瞬時に影響が伝わるため、たとえ素早く減衰したとしても、情報の伝達速度が無限大になる可能性があります。どのような条件で情報伝達速度が有限になるかは「線形光円錐問題」と呼ばれ、物理学における重要な未解決問題でした。

今回、共同研究チームは、量子多体系において長距離力が粒子間に存在するとき、情報伝達速度が有限になる一般的な条件を数学的に導きました。この条件は、数学的には「リープ・ロビンソン限界^[3]」で定式化される情報伝達速度の有限性のための条件で定式化されます。また、本研究で与えた条件が線形光円錐問題の最適解であることを証明しました。

本研究は、オンラインオープンアクセス科学雑誌『Physical Review X』に近日掲載予定です。

背景

情報化社会における最も重要な課題は、情報を効率的に速く伝達することです。高速な情報伝達には電磁波（光を含む）を使用しますが、光の速度は有限であるため、情報の伝達速度には原理的な限界が存在します。光速の有限性は、私たちが住む古典力学系^[4]の世界にさまざまな限界をもたらし、20世紀を代表する発見である相対性理論も、この光速の有限性を土台に記されています。

一方、古典力学系の世界を離れて量子力学系^[5]の世界に一歩足を踏み入れると、粒子は「粒」であり、また「波」でもあります。粒子がある場所に存在するという事象は確率的になり、粒子の存在は実験装置で「見る」まで確認できません。この粒子の存在確率は有限であるように見えることから、量子力学的な粒子は、古典力学の世界では許されない場所に光速を超えて移動できるようにも見えます（図1）。では、量子力学系において情報伝達速度は有限ではない、つまり情報伝達に限界は存在しないのでしょうか。

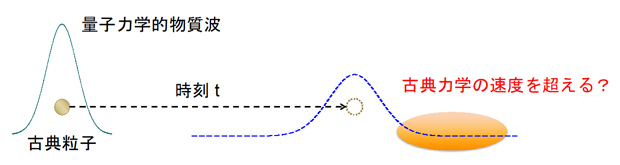
図1 量子力学における情報の伝達

ある点から別の点まで移動する際、古典粒子は必ず有限の速度（光速）を持つ。一方、量子力学では粒子は波のように振る舞い、どんなに遠く離れた点であっても有限の確率で粒子を検出できる可能性がある。はたして、量子力学では粒子が光速を超えて遠くに伝搬されることはあり得るのだろうか。

1972年にリープとロビンソンは、量子多体系において粒子間に短距離力が働くとき、情報伝達速度が有限であることを導き、古典力学系と同様に情報伝達に限界があることを示しました。この有限の情報伝達速度を「リープ・ロビンソン速度」、情報伝達の限界を「リープ・ロビンソン限界」といいます。また、このような情報伝達の性質は、情報を担う光が空間を広がるイメージとの類推から「線形光円錐」と呼ばれます（図2）。近年、量子コンピュータを用いた計算を行う際の必要量子回路数の計算や物質の低温特性の解明などにおいて、リープ・ロビンソン速度の有限性はますます重要になってきています。

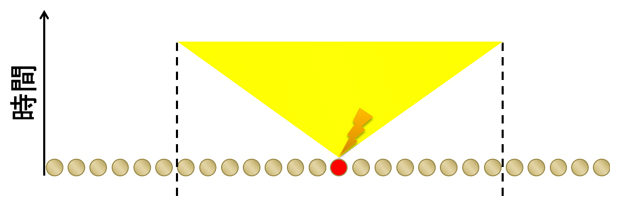
図2 線形光円錐の概要図（1次元）

特定の粒子（赤丸）に影響を与えると、その粒子に与えた影響は時間とともに他の粒子にも伝搬していく。相対性理論によると、その影響が届く粒子は光速で定義される線形光円錐内（黄領域）に限られる。「リープ・ロビンソン限界」は、非相対論的な量子多体系でも同様の線形光円錐を定義する。

一方で自然界には、重力や電子間に働くクーロン力をはじめ、水分子のような極性分子の間に働く力、ミクロな磁石の構成分子の間に働く力のように、遠くまで到達する力（長距離力）が存在します。長距離力は、距離に対してその大きさがべき乗則に従って小さくなるようなものを指し、一般に長距離力の大きさは、距離rの関数としてr^-α（αは正の定数で、働く長距離力の種類によって異なる）で表されます。

近年の冷却原子系^[6]の実験的な進展により、長距離力の減衰パラメータαを自在に制御できるようになってきました。長距離力が働く系では、二つの粒子が瞬時に影響し合えるため、たとえ素早く減衰したとしても、近い距離関係にある粒子間の情報伝達速度は無限大になってしまうように見えます。しかし、十分に離れた粒子間の力は非常に小さくなるため、αの値に応じて情報伝達速度が有限になる可能性があります。実際に、実験や数値シミュレーションで有限な情報伝達速度を観測した研究が数多く報告されています。

このような状況下、長距離量子多体系において、どのような条件で情報伝達速度が有限になるかは「線形光円錐問題」と呼ばれ、自然界の情報伝達における最も重要な未解決課題の一つになっていました。

研究手法と成果

リープ・ロビンソン限界は、数学的には時間発展を記述するユニタリー演算子^[7]に対して定義されます。そこで共同研究チームは、量子多体系に現れる長距離力を相互作用の距離に応じて分解し、分解された長距離力が、量子系の時間発展を記述するユニタリー演算子にどのように寄与するかを考えました。

各々のユニタリー演算子への寄与にだけ着目すれば、α>D+1（Dは空間の次元）の場合に、各々のユニタリー演算子が線形光円錐を保つことが既に証明されていますが、数学的な課題は、全てのユニタリー演算子の寄与を組み合わせたときに、線形光円錐が保たれるかどうかにあります。従来の理論予想では、分解された各々のユニタリー演算子が全て線形光円錐を保つのであれば、全てのユニタリー演算子を組み合わせた場合でも線形光円錐は保たれるはずだとされていました。言い換えると、α>D+1という条件が線形光円錐問題の答えであると予想されていました。しかし、これまで多種多様な理論的アプローチがあったにもかかわらず、αが無限大の場合を除き、線形光円錐問題の証明に成功した研究はありませんでした。

共同研究チームは、異なるユニタリー演算子を組み合わせたときに、リープ・ロビンソン限界の予想条件がどのように修正されるかについて、新しい数学的手法を開発しました。その手法を用いて、α>2D+1の条件であれば、線形光円錐が保たれることを数学的に証明しました。しかし、この条件（α>2D+1）は従来の予想の条件（α>D+1）に含まれるものであり、この段階ではまだ線形光円錐問題の完全な解決とは見なすわけにはいきませんでした。

そこで、α>2D+1という条件こそが正しく、従来の予想条件の方が間違っているのではないかと考えました。これを証明するためには、α<2D+1の場合に線形光円錐が保たれない状況が存在することを示す必要があります。そこで共同研究チームは、α<2D+1の場合に、量子多体系を介して任意の速度で情報を伝達できる例が存在することを具体的に示しました。

これら二つの結果を通して、α>2D+1の条件こそが線形光円錐問題の解であることが数学的に証明されました（図3）。

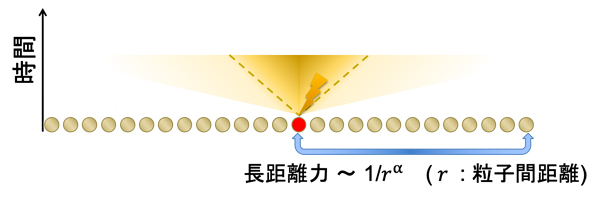
図3 有効な線形光円錐の概要図（1次元）

量子力学系で特定の粒子（赤丸）に影響を与えると、厳密な形での光円錐を定義できなくなる。この場合でも、有効的な線形光円錐（点線）が定義でき、影響が伝搬される粒子は近似的にこの光円錐内に制限される。長距離力は、距離に対してその強さがべき乗則に従って小さくなるようなものを指し、減衰を特徴づける指数をαで表現する。α>2D+1の場合には（Dは空間の次元、図の例ではD=1）、このような線形光円錐が常に存在することが示された。