2020-07-08 理化学研究所
理化学研究所(理研)脳神経科学研究センター数理脳科学研究チームのウーカシュ・クシミエシュ研究員、小川駿研究員、豊泉太郎チームリーダーの研究チームは、脳内の神経ネットワーク活動における臨界現象[1]である「カオス[2]の縁」と「雪崩現象」が同じ現象の異なる側面として理解できる神経ネットワークモデルとそれを解析するための理論を構築しました。
本研究成果は、外部からの刺激に鋭敏に応答する脳機能の理解や、臨界現象を応用して人工ニューラルネットワーク[3]の計算効率を高めるデザインの設計に貢献すると期待できます。
神経活動のダイナミクスを理解する上で、2種類の臨界現象が重要とされています。一つは、非カオス状態からカオス状態に転じる境界領域で観測される現象で、カオスの縁と呼ばれます。カオスの縁では、神経ネットワークの計算効率が高まることが報告されています。もう一つは、連鎖的に起こる神経活動の規模の分布がべき乗則[4]に従うために大きくばらつく現象で、雪崩現象といいます。しかし、この二つの臨界現象がどのように関係しているかは分かっていませんでした。
今回、研究チームは、従来の神経ネットワークモデルでは二つの臨界現象を同時に再現できないことを示しました。さらに、近年生理実験で計測されているシナプス強度[5]の確率が裾の厚い分布を示すモデルを解析するための理論を構築し、カオスの縁で雪崩現象が生じることを明らかにしました。
本研究は、科学雑誌『Physical Review Letters』オンライン版(7月7日付:日本時間7月8日)に掲載されます。
背景
脳内における神経活動のダイナミクスを理解する上で、2種類の臨界現象が重要とされています。臨界現象とは、二つの性質の異なる状態の境界領域で観測される特殊な現象のことです。
臨界現象の一つは、神経活動のダイナミクスが非カオス状態からカオス状態に転じる境界領域で観測される現象で、「カオスの縁」と呼ばれています(図1)。非カオス状態の場合は、神経活動が少し乱されても将来の神経活動に大きな差は生じませんが、カオス状態の場合は、神経活動が少し乱されると、その影響が時間とともに拡大し、将来の神経活動には大きな差が生じることになります。カオスの縁では、神経ネットワークの計算効率が高まると報告されています。
もう一つは、神経ネットワーク上で連鎖的に引き起こされる神経活動の規模(活動時間や細胞数)の分布がべき乗則に従うために大きくばらつく現象で、「雪崩現象」と呼ばれています(図1)。一つの神経細胞が次の時刻に活動させる神経細胞の数が平均的に1未満の場合、連鎖的活動は指数関数的に減衰していき、1より大きい場合は指数関数的に増大していきます。これらの境界領域、つまり、次の時刻に活動させる神経細胞の数が平均的にちょうど1となる場合、規模はべき分布[4]に従い、規模の大きな連鎖活動や小さな連鎖活動が生じます。
脳は臨界現象を示す境界領域付近で機能しているのではないかと考えられていますが、一般的には、カオスの縁と雪崩現象は別の現象であることが分かっています。また、これまで、これらの臨界現象の研究には別々の神経ネットワークモデルが使用されてきたため、二つの臨界現象の関係はよく分かっていませんでした。
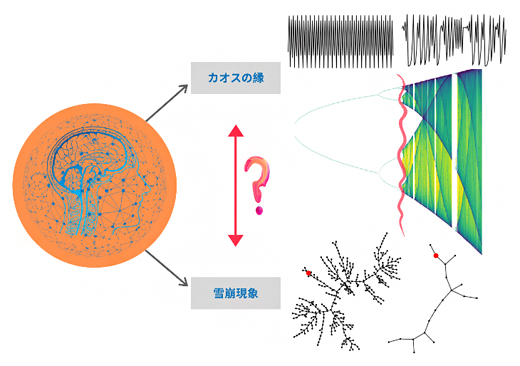
図1 脳内の神経ネットワーク活動における二つの臨界現象
右上:カオスの縁の模式図。神経ネットワーク活動のダイナミクスがカオス状態になると、活動が不規則になる。
右下:雪崩現象の可視化。トリガーとなる神経細胞(赤点)を始点として引き起こされる一連の神経活動。直接活動を引き起こした神経細胞を黒い線で結んだ。トリガーとなる神経細胞に応じて、規模の大きな連鎖活動や小さな連鎖活動が生じる。
研究手法と成果
脳内で神経細胞は、他の多数の神経細胞からシナプスを介して信号を受け取り、強い入力を受けると自ら活動して次の神経細胞へ信号を伝えます。この多数の神経細胞間における信号伝達を数学的に模した数理モデルを「神経ネットワークモデル」、シナプスが信号を出したときに、次の神経細胞に与える影響の強さを「シナプス強度」といいます。
従来の研究では、解析のしやすさから、シナプス強度の確率分布がガウス分布を示す神経ネットワークモデルが研究されてきました。ガウス分布では、確率密度関数の裾が指数関数的に急速に減衰します(図2)。
研究チームはまず、このシナプス強度がガウス分布に従う神経ネットワークモデルを解析しました。このモデルでは、シナプス強度が強くなるにつれて、非カオス状態とカオス状態が共存し、非カオス状態からカオス状態への不連続な転移(不連続相転移[1])が起こります。解析の結果、非カオス状態とカオス状態が離れているため、一旦転移が起こると元の状態には容易に戻れないことから、神経ネットワークの状態をカオスの縁に安定して保つことは困難であることが分かりました。
また、このモデルでは雪崩現象も観測できませんでした。シナプス強度の確率分布がガウス分布を示す場合、各シナプス強度はほとんど同じで、強度が桁違いに大きいシナプスは滅多に存在しません。そのため、同程度の強さのシナプスが協調して働くことで、神経細胞を活動させます。このモデルでシナプス強度を全体的に弱くすると、神経活動を維持できず活動が消えてしまい、反対に、シナプス強度を全体的に徐々に大きくすると、あるところで一気に多数の神経細胞が協調して次の神経細胞を活動させる状態に転移します。従ってこのモデルでは、雪崩現象で想定しているような一つの神経細胞が次の時刻に平均的に一つの神経細胞を活動させるという状況は生じません。
一方で近年、生理実験によってシナプス強度の確率分布が計測され、裾がガウス分布よりも厚い分布を示すことが報告されています。そこで、シナプス強度の分布がべき分布の一種であるコーシー分布[4]を示す神経ネットワークモデルと、それを解析する理論を構築しました(図2)。すると、構築したモデルでは、シナプス強度が一定以上に強くなると、神経ネットワーク全体の活動度がゼロから連続的に上昇することが分かりました。それに伴い、非カオス状態からカオス状態への転移が連続的に起こり(連続相転移[1])、神経ネットワークの状態をカオスの縁に安定して保持できることが分かりました。さらに、このカオスの縁では、一つの神経細胞が他の一つの神経細胞を活動させるという条件が満たされ、雪崩現象が生じることが示されました。
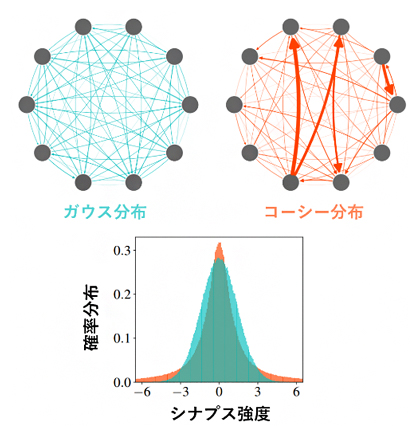
図2 神経ネットワークの模式図(上)とシナプス強度の確率分布(下)
上:シナプス強度がガウス分布とコーシー分布である二つの神経ネットワーク。黒丸が神経細胞を、矢印がシナプス結合(太さは強度の絶対値)を表す。
下:二つのシナプス強度の確率分布を示す。緑がガウス分布、赤がコーシー分布である。コーシー分布の方が、ガウス分布よりも分布の裾が厚い。
今後の期待
本研究では、これまで神経ネットワークで研究されてきたカオスの縁と雪崩現象が、同じ臨界現象の別の側面として理解できることを示しました。神経ネットワークは、カオスの縁において計算能力が高まるとの研究が報告されています。また、雪崩現象で特徴づけられるような脳の自発的活動が脳機能とどのように関係するかに関しても研究が進んでいます。今回構築したモデルおよび理論は、臨界現象と脳の情報処理との関係を理解する上で今後重要な役割を果たすと期待できます。
またカオスの縁や雪崩現象は、神経ネットワークに限らず、一般の物理システムでも広く研究されている概念です。脳がそれらをどのように利用しているかにヒントを得ることで、高感度のIoTネットワークを設計したり、計算効率のより高い人工ニューラルネットワークを構築したりすることが将来可能になるかもしれません。
補足説明
1.臨界現象、不連続相転移、連続相転移
物理学において「相転移」とは、温度などの変化によって物質が一つの相から別の相へ転移する現象である。相転移は二つの相が共存する状態を伴う「不連続相転移」と、そうではない「連続相転移」がある。「臨界現象」は連続相転移に伴って起こる現象であり、ある物理量の発散などの異常な振る舞いや、特徴的な長さや時間スケールが発散して存在しなくなるなどの特異的な現象が起こる。
2.カオス
システムが決定論的な規則によって時間発展しているのにも関わらず、一見不規則に見える複雑な振る舞いを示す状態のこと。決定論的な規則に従うシステムでは、初期状態を決めるとその後の振る舞いが一意に定まる。しかしカオスの場合は、その初期状態にわずかでも誤差が乗ると、その誤差の影響が時間とともに拡大し、後に全く異なる値を予測してしまう。この性質を初期値鋭敏性と呼び、予測の困難性につながる。また、初期値鋭敏性はバタフライ効果とも呼ばれる。これは、エドワード・ローレンツの気象モデルが初期値鋭敏依存性を示したことから、一匹の蝶が飛んで気流を乱すと将来の気象が全く違うものになるというカオスの性質を標語的に表したものである。
3.人工ニューラルネットワーク
神経細胞を模した計算ユニット(ニューロン)と、それらをつなぎ信号を伝達する役割を担う結合(シナプス)からなる数理モデルのこと。脳内の神経ネットワークの数理モデル化を端緒としているが、AI分野(機械学習分野)においてよく用いられている。近年注目を集めている深層学習は、ニューロンを配置した層を深く重ねた人工ニューラルネットワークで、与えられたデータを再現するように各層をつなぐシナプス強度を学習する技術である。
4.べき乗則、べき分布、コーシー分布
変数xのべき乗をxaと表し、実数aのことを指数と呼ぶ。累乗(x2など)は、べき乗の指数が自然数の特殊な場合である。ガウス分布では、確率密度関数p(x)の裾が指数関数的に急速に減衰するのに対し、「べき分布」ではべき的に(aを正の実数として、|x|-aに比例して)緩やかに減衰する。べき分布は裾が厚いために、べき分布に従う量は非常に大きな値を取ることがある。べき分布の一例として、「コーシー分布」があるが、分布の裾が厚いために分散の値が無限大となる。観測量がべき分布を示すような現象を「べき乗則」に従っているといい、雪崩現象はその一例である。べき乗則に従う現象では、多くの小規模な事象と少数ではあるが非常に大規模な事象が、同じ機構により発生する。地震の発生頻度と規模もべき乗則に従うといわれている。
5.シナプス強度
シナプスとは脳の神経細胞をつなぐ接合部位で、神経細胞間の信号伝達を担う。シナプスが伝達物質を放出したときに、次の神経細胞に与える影響の強さをシナプス強度と呼ぶ。
研究支援
本研究は、日本医療研究開発機構(AMED)「革新的技術による脳機能ネットワークの全容解明プロジェクト」、日本学術振興会(JSPS)科学研究費助成事業新学術領域研究(研究領域提案型)「マルチスケール精神病態の構成的理解(領域代表者:林(高木)朗子)」による支援を受けて行われました。
原論文情報
Łukasz Kuśmierz, Shun Ogawa, Taro Toyoizumi, “Edge of chaos and avalanches in neural networks with heavy-tailed synaptic weight distribution”, Physical Review Letters, 10.1103/PhysRevLett.125.028101
発表者
理化学研究所
脳神経科学研究センター 数理脳科学研究チーム
研究員 ウーカシュ・クシミエシュ(Łukasz Kuśmierz)
研究員 小川 駿(おがわ しゅん)
チームリーダー 豊泉 太郎(とよいずみ たろう)
報道担当
理化学研究所 広報室 報道担当