次世代のスパコン設計を模した40万頂点数の巨⼤グラフを発⾒

通信遅延の⼤幅な低下などの実⽤に期待 〜効率的なスパコン設計につながるグラフ発⾒を競うコンペ「グラフ ゴルフ」で〜

2018/11/27 国⽴情報学研究所

⼤学共同利⽤機関法⼈ 情報・システム研究機構 国⽴情報学研究所（NII、所⻑︓喜連川 優、東京都 千代⽥区）は、複雑なネットワーク構成をスイッチ間の接続関係を表す簡単なグラフ(*1)に抽象化し、より単純な構成のグラフの発⾒を競うコンペティション「グラフゴルフ」(*2)で優れたグラフを発⾒した３名の個⼈と１チームを、本⽇11⽉27⽇、岐⾩県⾼⼭市で開催された国際シンポジウム 「CANDAR2018」(*3)で表彰しました。

これらのグラフは、効率的なプロセッサーコア間の通信や、スーパーコンピューター（スパコン）の超並列計算の最⻑通信時間の最⼩化、次世代のスパコン設計の通信遅延の低下など、性能向上への応⽤が期待されます。また今回、表彰者の⼀⼈である北須賀 輝明が発⾒した4つのグラフが、グラフ理論分野において著名な問題とされてきた次数直径問題の最⼤グラフ (*4)の記録更新になるという新たな展開が⽣まれ、グラフに関する理論分野にも貢献しています。

最近のコンピューターは⼤規模で複雑になってきており、特にスパコンでは1千万以上のプロセッサ ーコア（以降、コアと表記）が接続されるものも登場しています。しかし、⼀つのコアに直接接続できるコアには制限があることから、コア間のネットワーク構成を⼯夫して膨⼤な数のコアを効率的に相互接続することが、スパコンの処理能⼒に⼤きく影響します。本コンペでは、スパコンの専⾨家でなくても参加ができるように、実際のスパコンのネットワークを抽象化した数学的なグラフに置き換えて、効率的なネットワーク構成の発⾒を競いました。

具体的にはコアに直結しているスイッチを「頂点」、コアとコアをつなぐ配線を「辺」とみなしたグラフとして、ネットワーク構成をモデル化しました。実際のスパコンのネットワーク設計では、スイッチあたりの接続コア数、ルーティング、スイッチング⽅式をはじめとする多くの検討項⽬がありますが、本モデルから対象ネットワーク構成の最短経路利⽤時のすべてのスイッチ間の通信遅延を⾒積ることができます。そして、問題設定で指定された頂点数と「次数」（⼀つの頂点から出る辺の数）で構成されるグラフの中で、⼀つの頂点から最も離れた頂点までの「ホップ数」（経路上の辺の数）および各頂点間のホップ数の平均値が最も⼩さいグラフの発⾒を競いました。このようなグラフをコンピューターで発⾒する単純な⽅法は、計算ツールを⽤いてすべてを列挙することですが、例えば、頂点数12、次数4のグラフは4,800億個もあり、現在の計算機の性能ではこれ以上⼤きな頂点数を扱うことは困難です。

第4回となる本コンペは5⽉〜10⽉に実施し、国内外から239件の有効応募がありました(*5)。その結果、優れたグラフを発⾒した中尾 昌広（理化学研究所計算科学研究センター）、⼩泉 透（東京⼤学）、EvbCFfp1XB（ユーザ名）の個⼈3名と、北須賀 輝明（広島⼤学）と飯⽥ 全広（熊本⼤学）との連合チームを表彰しました。（1）頂点数72、次数4の理想のグラフ、（2）最も離れた頂点までのホップ数を最⼩にした頂点数3,019、次数30のグラフ、（3）平均ホップ数が理論限界(*6)に迫る頂点数40万の巨⼤グラフなど、実⽤上重要な発⾒が得られました。それぞれの特徴は以下の通りです。

1. 実際のプロセッサーチップ（それぞれが72コア搭載）の内部ネットワークを模したグラフ構成を出題し、各コアを頂点（72頂点）として、直径4、平均ホップ数3未満で効率的に接続できることが分かりました（3ページ図）。本グラフはチップ上にレイアウトした時に⼀部の配線が⻑くなる場合がありますが、先⾏研究成果から性能劣化なしでネットワークを動作させる技術があるため、効率的なプロセッサーコア間の接続が実装可能であるといえます。
2. 実際のスパコンのネットワークを模した問題を出題し、最⻑ホップ数を最⼩にするネットワーク設計が可能であることが分かりました。スパコンの超並列計算のボトルネックとなることが多い最⻑通信時間を最⼩化できる可能性があります。
3. 次世代のスパコン設計は10万ノード以上（1 ノードあたり100 プロセッサコア以上）が想定されるため、本コンペでは初めて40万ノードのネットワーク構成を出題しました。今回の成果は、通信遅延を⼤幅に低下させることが期待できる巨⼤ネットワーク構成の解の⼀つを⽰した点で有益といえます。

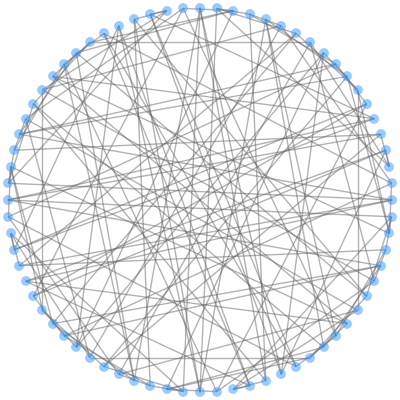
図：頂点数72、次数4の理想グラフ（中尾 昌広）

これらのグラフは、効率的なプロセッサーコア間の通信や、スパコンの超並列計算の最⻑通信時間の最⼩化、スパコン設計の通信遅延の低下など、実⽤への応⽤が期待されます。また今回、表彰者の北須賀 輝明が発⾒した4つのグラフが、グラフ理論分野の著名な問題である次数直径問題の最⼤グラフの記録更新になるという新たな展開が⽣まれ、理論分野の活性化にも貢献しています。

過去3回のコンペの各表彰者の⽅々の全⾯的なご協⼒により、グラフゴルフに関連した国内外のイベントでの発表資料をホームページ上にて公開することで、様々な優れたグラフの構成⽅法を分かりやすく解説しています。

「グラフ ゴルフ」の成果は、通信遅延を削減することを重視する最近のスパコンや計算機プロセッサーチップのネットワーク構成の設計への直接的な利⽤が期待されています。本コンペは問題の条件設定を変えて今後も継続する予定で、グラフ（ネットワーク構成）のカタログを「Graph Bank」 (*7)に蓄積していくことで学術界や産業界に貢献していきます。（⽂中敬称略）

ニュースリリース（PDF版）

次世代のスパコン設計を模した40 万頂点数の巨⼤グラフを発⾒／通信遅延の⼤幅な低下などの実⽤に期待
〜効率的なスパコン設計につながるグラフ発⾒を競うコンペ「グラフ ゴルフ」で〜