特定の経路を転がる形状を作る新しいアルゴリズムを考案 Scientists devise a new algorithm to make shapes that roll in specific paths
2023-09-11 韓国基礎科学研究院(IBS)
◆物体は、磁気や医療診断技術においても重要な役割を果たす「回転」プロパティを活用し、磁場やラジオ波との相互作用を通じて特定の軌道をたどります。このトラジェクトイドアルゴリズムは、MRIの精度向上にも役立つ可能性があります。
<関連情報>
- https://www.ibs.re.kr/cop/bbs/BBSMSTR_000000000738/selectBoardArticle.do
- https://www.nature.com/articles/s41586-023-06306-y
所望の経路に沿って転がるように形作られた固体の軌跡 Solid-body trajectoids shaped to roll along desired pathways
Yaroslav I. Sobolev,Ruoyu Dong,Tsvi Tlusty,Jean-Pierre Eckmann,Steve Granick & Bartosz A. Grzybowski
Nature Published:09 August 2023
DOI:https://doi.org/10.1038/s41586-023-06306-y
Abstract
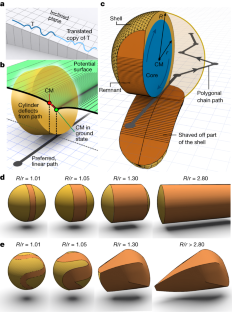
In everyday life, rolling motion is typically associated with cylindrical (for example, car wheels) or spherical (for example, billiard balls) bodies tracing linear paths. However, mathematicians have, for decades, been interested in more exotically shaped solids such as the famous oloids1, sphericons2, polycons3, platonicons4 and two-circle rollers5 that roll downhill in curvilinear paths (in contrast to cylinders or spheres) yet indefinitely (in contrast to cones, Supplementary Video 1). The trajectories traced by such bodies have been studied in detail6,7,8,9, and can be useful in the context of efficient mixing10,11 and robotics, for example, in magnetically actuated, millimetre-sized sphericon-shaped robots12,13, or larger sphericon- and oloid-shaped robots translocating by shifting their centre of mass14,15. However, the rolling paths of these shapes are all sinusoid-like and their diversity ends there. Accordingly, we were intrigued whether a more general problem is solvable: given an infinite periodic trajectory, find the shape that would trace this trajectory when rolling down a slope. Here, we develop an algorithm to design such bodies—which we call ‘trajectoids’—and then validate these designs experimentally by three-dimensionally printing the computed shapes and tracking their rolling paths, including those that close onto themselves such that the body’s centre of mass moves intermittently uphill (Supplementary Video 2). Our study is motivated largely by fundamental curiosity, but the existence of trajectoids for most paths has unexpected implications for quantum and classical optics, as the dynamics of qubits, spins and light polarization can be exactly mapped to trajectoids and their paths16.