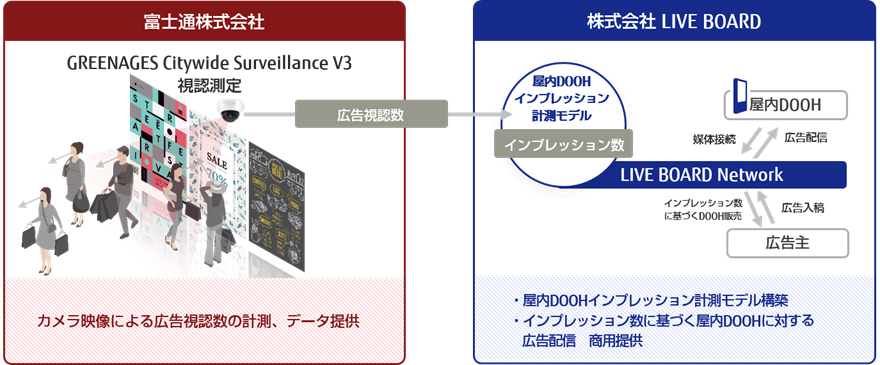
2020-07-08 理化学研究所
理化学研究所(理研)数理創造プログラムの横倉祐貴上級研究員らの共同研究チームは、量子力学[1]と一般相対性理論[2]を用いて、蒸発するブラックホールの内部を理論的に記述しました。
本研究成果は、ブラックホールの正体に迫るものであり、遠い未来、情報[1]を蓄えるデバイスとしてブラックホールを活用する「ブラックホール工学」の基礎理論になると期待できます。
近年の観測により、ブラックホールの周辺のことについては徐々に分かってきましたが、その内部については、極めて強い重力によって信号が外にほとんど出てこられないため、何も分かっていません。また、ブラックホールは「ホーキング輻射[3]」によって最終的に蒸発することが理論的に示されており、内部にあった物質の持つ情報が蒸発後にどうなってしまうのかは、現代物理学における大きな未解決問題の一つです。
今回、共同研究チームは、ブラックホールの形成段階から蒸発の効果を直接的に取り入れた理論的解析を行い、「物質の量子力学の効果を含むアインシュタイン方程式[4]」の新しい解を得ました。その結果、ブラックホールはイベントホライズン[5]を持たない高密度な物体であることがわかりました。これは、ブラックホールはあらゆる物体が強い重力の下で取り得る極限的状態であることを示しています。この解はブラックホール内部の物質と時空を直接記述することができるため、内部に入った物質の情報を追跡できます。今後の研究により、蒸発後にその情報がどうなるのかを理解できる可能性があります。
本研究は、オンライン科学雑誌『Universe』(6月4日付)に掲載されました。

強重力下ではどんな物体も極限的状態としてブラックホールになり、情報デバイスになる可能性がある
背景
質量(エネルギー)を持つ全ての物質は、万有引力によって互いに引き合っています。そのため、物質が集まり非常に高密度になると、自身の重力に耐えきれずつぶれてしまいます。その結果として作られる物体が「ブラックホール」です。
重力を時空の曲がりとして記述する一般相対性理論に基づくブラックホールは、重力が非常に強いため時空が極端に曲がった、光さえも脱出できない真空の領域です。ブラックホールとその外側の境界を「イベントホライズン[5]」といい、その半径はブラックホールのもととなった物質の質量(エネルギー)で決まり、「シュワルツシルト半径[6]」と呼ばれます。
近年の観測により、ブラックホールの周辺のことは徐々に分かってきました。しかし、ブラックホールの内部からの信号はイベントホライズンから外に出てこられないため、その内部のことは何も分かっていません。
ところで、物理学において私たちの世界は、時空を記述する一般相対性理論と、物質を構成する電子や陽子などの微視的な物理現象を記述する量子力学の二つの理論によって記述されます。したがって、重力が強く物質から作られるブラックホールに対しては、一般相対性理論だけでなく量子力学も重要なはずです。
量子力学の効果が加わると、ブラックホールの様相が一変します。曲がった時空の持つエネルギーと真空の量子力学的効果によって、ブラックホール近くの真空から光の粒子(光子)が作られ、徐々に放出されます。これを「ホーキング輻射」といいます。ホーキング輻射により、ブラックホールの質量は徐々に減っていき、最終的には蒸発してしまうと考えられています。
では、ブラックホールの蒸発後、その内部にあった物質の持つ情報はどうなってしまうのでしょうか。一見すると、内部の情報はイベントホライズンに閉じ込められ出てこられないにもかかわらず、ブラックホール自体は蒸発により消えてしまうため、情報は消失するように思えます。もしそうならば、それは「情報は必ず保存される」という量子力学の原理に反することになります。これは「情報問題」と呼ばれ、現代物理学における大きな未解決問題の一つです。情報問題は、「ブラックホールとはいったい何か?」を考え直させる原理的な問題であるともいえます。
研究手法と成果
共同研究チームは、蒸発の効果を最初から取り入れて、物質が重力でつぶれていく過程を理論的に解析しました。
球状の物質でこの過程を考えてみましょう(図1A)。連続的に分布した球状物質を、たくさんの球状の層の集まりと見なします(図1A1)。各層は、多くの粒子から成るはずです(図1A2)。その中の一つの粒子が重力により引かれ、中心に落下している様子を考えます(図1A3)。その重力は、粒子より内側にある物質のエネルギーによって決まります。そのエネルギーに相当するシュワルツシルト半径(図1A3の赤い破線)は、ホーキング輻射によりエネルギーが減っていくために時間とともに小さくなります。このとき、落下してきた粒子がシュワルツシルト半径の近くまでやってくると、落下と蒸発の効果が釣り合って、蒸発が先に生じている分だけ、粒子はシュワルツシルト半径に届きません(図1A3)。その結果、粒子はシュワルツシルト半径を通り越さず、そのわずかに外側のある所に近づいていきます。
これと同じことが球状物質のあらゆる所で生じ、この物質全体は収縮して、中身の詰まった高密度な物体ができあがります(図1B)。特に、最も外側の層を成す粒子たちは、全エネルギーに相当するシュワルツシルト半径のわずかに外側の所に近づいていくため、それがこの高密度な物体の表面になります。このイベントホライズンを持たない高密度な物体がブラックホールです。表面の半径とシュワルツシルト半径の差がわずかであるため、外からは、これまで考えられてきたブラックホールのように見えます。そして、非常に長い時間が経過した後、最終的には蒸発してしまいます(図1C)。
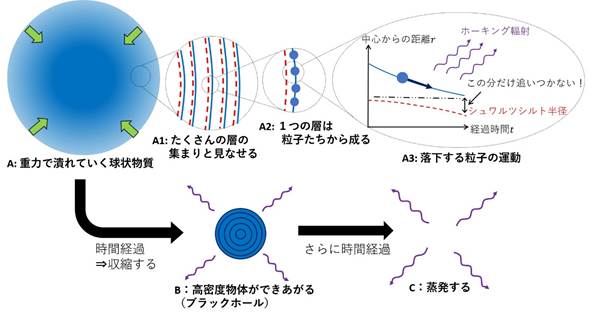
図1 物質の量子力学の効果を取り入れたブラックホールの形成と蒸発
重力でつぶれていく球状物質の内部を表す時空計量[2]と波動関数[1]を、物質の量子力学の効果を含むアインシュタイン方程式である「半古典的アインシュタイン方程式[4]」の解として構成したところ、上記の描像が示されました。その解には特異点[5]は現れず、また、真空の量子力学的効果により発生した大きな圧力が物質を支えていることが分かりました。
図1のAからBは、重力が極限的に強くなり物質が「凝集する」過程であり、それは水分子が水蒸気(気体相[7])から水(液体相)になる過程に似ています。また、BからCの蒸発過程は、逆に水が水蒸気に変化することに相当します。この現象は、万有引力により全ての物質に対して普遍的に生じます。その意味で、ブラックホールとは、あらゆる物質が強い重力下で極限的にとる状態、すなわち「ブラックホール相」だといえます。
この解では、物質がブラックホール内部にどのように分布しているのかが分かるため、その情報(波動関数)がどこにあるのかを特定することができます。実際に、情報が内部で取り得るパターンの総数(情報量、エントロピー[8])を調べると、それは熱力学[8]から導かれる結果「ベッケンシュタイン・ホーキング公式[9]」に一致します。これは、本研究で得られたブラックホールの内部構造が、これまで知られていたブラックホール外部の振る舞いと整合的であることを意味しています。
今後の期待
本研究により明らかになったブラックホールの描像は、全く新しい未来を提示しています。まず、情報問題が解決されるかもしれません。ブラックホール内部に分布している物質の情報(波動関数)の時間発展を詳しく調べることにより、蒸発後に情報がどのように戻ってくるのかを解明できる可能性があります。
また、このブラックホールは通常の星のように表面を持つため、イベントホライズンを持つ従来のブラックホールとは、天体現象の信号が異なるはずです。将来の観測技術の向上により、その違いが確認され、この理論が検証されると考えられます。
さらに、このブラックホールは内部構造を持ち、もととなった物質の情報がどのように保存されているのかが分かります。したがって、もし情報がどのように戻って来るのかが今後明らかになれば、遠い未来ではブラックホールは大量の情報を保存する情報ストレージとして活用できるかもしれません。本研究成果は、このような「ブラックホール工学」の基礎理論になると期待できます。
補足説明
1.量子力学、情報、波動関数
量子力学は、物体を構成する電子や陽子などの微視的な物理現象を記述する物理法則であり、物質の状態は波動関数で記述される。波動関数は物質の情報を表し、その情報は時間が経過しても保存される。
2.一般相対性理論、アインシュタイン方程式、時空計量
一般相対性理論は、重力を時空の曲がりとして記述する物理法則である。エネルギーがあると時空が曲がり、その曲がりに沿って物質は運動する(これが重力下の物体の自由落下に相当する)。その基礎方程式「アインシュタイン方程式」は「時空の曲がり=物質のエネルギー分布」を表し、時空の曲がりを定める時空計量を決定する。
3.ホーキング輻射
ブラックホールが形成される過程において、時間変化する曲がった時空の効果と真空の量子的効果により、ブラックホール近くの真空から光の粒子(光子)が生成され放出される。これをホーキング輻射という。1974年、スティーブン・ホーキングにより理論的に示された。ホーキング輻射によりブラックホールのエネルギーは減少していき、その結果ブラックホールは蒸発すると考えられている。
4.物質の量子力学の効果を含むアインシュタイン方程式、半古典的アインシュタイン方程式
アインシュタイン方程式において、物質の量子力学の効果を取り入れた方程式のこと。半古典的アインシュタイン方程式と呼ばれる。物質のエネルギー分布を量子力学的に扱い、時空の曲がりを一般相対性理論の時空計量により記述する。
5.イベントホライズン、特異点
量子力学を考慮せず一般相対性理論だけに従う場合、物質が集まり非常に高密度になると、自身の重力に耐えきれず中心の一点につぶれる。その点はエネルギー密度や時空の曲がりが無限大となり、特異点と呼ばれる。その周囲は、重力が非常に強いため、光でさえも登れないほど急激な時空の曲がりを持つ真空領域となる。光が遠くに逃げられるかどうかの時空の境界をイベントホライズンという。このイベントホライズンの内側の時空領域が、量子力学を考慮しない場合のブラックホールである。特に、球状のブラックホールの場合、イベントホライズンの空間半径はシュワルツシルト半径である。
6.シュワルツシルト半径
ある質量を持つ球状の物質を考えたとき、それ以上小さくすると重力の効果が顕著になり始める半径のこと。それは質量に比例して決まる(例:地球の質量の場合、約1cmとなる)。シュワルツシルト半径は、ブラックホールに限らずどんな物質にも定義できる。もし物質の分布する半径がシュワルツシルト半径よりも小さくなると、イベントホライズンが生じる。
7.相
容器に少し水を入れて蓋をして放置すると、(温度や体積にもよるが)水と水蒸気が共存する。このように、同一の物質組成でありながら、異なる状態にある二つの均質部分が互いに接して共存することがある。このような状態を物質の相という。本研究の場合は、「ブラックホール相」と「物質相」である。
8.エントロピー、熱力学
エントロピーは、物質を構成する微視的要素が、与えられたエネルギーや体積の下で、何パターンの構成の仕方があるのか(何パターンの波動関数を取り得るか)を表す量である。これは、そのエネルギーや体積の下で、その物質が最大でどれだけ多くの情報を原理的に蓄えることができるのか(情報量)を表す。熱力学は、微視的構成要素の詳細に依らない物体の普遍的な法則を与える物理法則である。熱力学では、エントロピーは、物体に対する操作・変化の不可逆性を特徴づける量として導入される。
9.ベッケンシュタイン・ホーキング公式
プランク長(おおよそ10-35m)は、時空の長さの解像度の限界だと考えられている。ブラックホールの表面積をプランク面積(おおよそ10-70m2)で割った量を1/4倍したものがブラックホールのエントロピーであると、ブラックホールに対する熱力学により予言されている。これをベッケンシュタイン・ホーキング公式という。ブラックホールは3次元空間の物体であるにもかかわらず、その情報量は表面積に比例するという不思議な性質を持つ。本研究は、この公式をブラックホール内部の微視的構造から再現した。
共同研究チーム
理化学研究所 数理創造プログラム
上級研究員 横倉 祐貴(よこくら ゆうき)
京都大学大学院 理学研究科 物理学宇宙物理学専攻
教授 川合 光(かわい ひかる)
研究支援
本研究は、日本学術振興会(JSPS)学術研究助成基金助成金若手研究「物質と重力のダイナミクスに基づく蒸発するブラックホールの場の理論的定式化(研究代表者:横倉祐貴)」による支援を受けて行われました。
原論文情報
Hikaru Kawai and Yuki Yokokura, “Black Hole as a Quantum Field Configuration”, Universe, 10.3390/universe6060077
発表者
理化学研究所
数理創造プログラム
上級研究員 横倉 祐貴(よこくら ゆうき)
報道担当
理化学研究所 広報室 報道担当