2021-03-08 理化学研究所
理化学研究所(理研)革新知能統合研究センター汎用基盤技術研究グループ数理科学チームの桑原知剛研究員らの国際共同研究チームは、量子力学に従う多粒子系(量子多体系[1])が有限温度[2]下で示す「量子もつれ[3]」に関する新たな法則を発見しました。
本研究成果は、虚数の時間発展[4]で生成される量子もつれに関する新たな知見を与えると同時に、量子シミュレーション[5]や量子機械学習[6]などの分野における効率的手法の開発に貢献すると期待できます。
量子多体系が示す「量子熱平衡状態[7]」における量子もつれの性質は、「境界則」と呼ばれる普遍法則に従うことが知られています。これは、系を二つの領域に分割したとき、領域間の量子もつれの大きさが境界の大きさ(面積)に比例するという法則です。境界則は、室温下では普遍的に成り立つことが証明されています。一方、低温下では温度Tが絶対零度(0ケルビン)に近づくにつれて、温度の逆数(T-1)に比例して破れていくとこれまで考えられていました。
今回、国際共同研究チームは、境界則が従来の予想に反して温度Tの逆数の2/3乗(T-2/3)に比例して破れていくことを新たに示しました。さらにこの性質をもとに、低温下での量子多体系の量子熱平衡状態をシミュレートする新手法を開発し、必要な計算時間を従来よりも大幅に短縮することに成功しました。
本研究は、オンライン科学雑誌『Physical Review X』(3月9日付)に掲載されます。
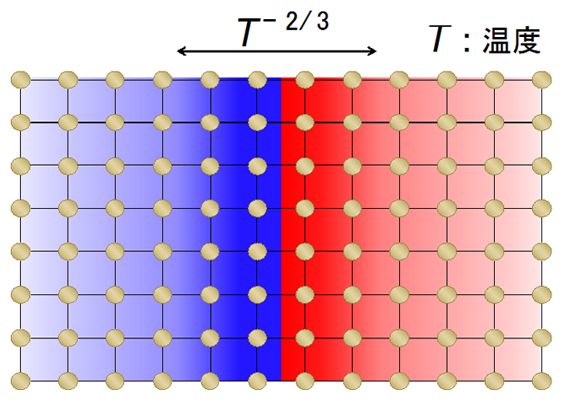
有限温度における量子もつれの境界則は、低温下では温度Tの逆数の2/3乗に比例して破れる
背景
量子力学に従って運動する多数の粒子系(量子多体系)は、一般的に「量子もつれ」と呼ばれる奇妙な相関を持つことが知られています。この量子もつれの性質を利用して、従来よりも計算速度の速いコンピュータを作ろうという試みが量子コンピューティングと呼ばれる分野です。量子コンピューティングにおいて、最も重要な研究対象の一つが「量子熱平衡状態」(量子ギブス状態)のシミュレーションです。量子熱平衡状態とは、ある温度Tの熱浴(一定の温度を保っている十分大きな外界)に接した量子多体系が長時間の後に到達する典型的な状態を指します(図1)。量子熱平衡状態の効率的なシミュレーションは、量子シミュレーションや量子機械学習の高速化において主要な役割を果たします。
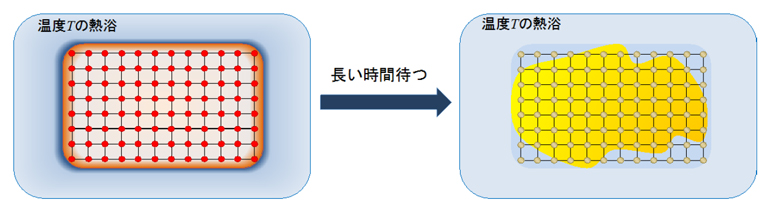
図1 量子熱平衡状態
ある温度Tの熱浴に接した量子多体系は十分に長い時間が経つと、マクロに見て変化しない状態(量子熱平衡状態)へと至る。一般に、量子熱平衡状態は量子的に見て複雑にもつれた状態になっている。
それでは、量子熱平衡状態のシミュレーションはどの程度困難な問題なのでしょうか。それを特徴づけるのが、量子熱平衡状態に存在する量子もつれの大きさです。一般的に、量子もつれが大きければ大きいほど、シミュレーションが困難になることが知られています。したがって、シミュレーションの難しさを理解するには、量子もつれの構造を理解する必要があります。これまで、量子熱平衡状態は「境界則」と呼ばれる普遍法則を満たすことが知られていました。これは図2に示すように、量子多体系を二つの領域に分割したとき、二つの系のもつれの大きさ[8]は境界の大きさ(面積)にほぼ比例するという法則です。
量子もつれの境界則は、室温下では普遍的に成り立つことが数学的に証明されていますが、絶対零度(0ケルビン)を含む低温下では破れてしまうことが知られています。量子もつれの境界則が低温になるにつれてどのように破れていくかは、量子熱平衡状態のシミュレーションの観点から大きな注目を集めています。先行研究では、量子もつれは温度Tの逆数(T-1)に比例して境界の外へ浸食していく、つまり境界則は破れると予想されていました。そこで共同研究チームは、低温下での量子もつれに関する従来の予想が正しいかどうか確かめました。
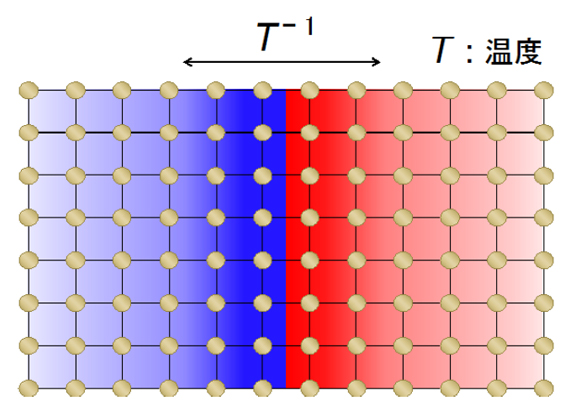
図2 従来の有限温度の境界則の予想
量子多体系を二つの領域(青領域と赤領域)に分割したとき、二つの領域間に存在する量子もつれの大きさは境界の大きさ(面積)に比例する。一方で、量子もつれの境界則は温度が低くなっていくと、温度Tの逆数(T-1、1/T)に比例して(つまり反比例して)破れていくと予想されていた。
研究手法と成果
有限温度Tにおける量子もつれは、虚数時間の時間発展によって生成される量子もつれと密接な関係があります。現実世界では実数の時間が流れていますが、量子力学では虚数の時間発展を定義することができます。虚数の時間発展は数学で定義される架空の概念にとどまらず、実際に、量子コンピュータを用いて、虚数の時間発展をシミュレートする実験も近年行われています。
虚数の時間発展を用いることで、図1で紹介した方法とは異なる方法で、量子熱平衡状態を得ることができます。図3に示すように、初期状態として量子もつれがない一様な分布を取ってきて、その状態を虚数時間i/(2T)だけ時間発展させると、温度Tの量子熱平衡状態になります(iは虚数単位)。したがって、「虚数の時間発展によってどの程度の量子もつれが生成されるのか」を理解できれば、有限温度における量子もつれの量も理解できます。
実数の時間発展で生成される量子もつれの大きさは、時間の長さに比例することが既に分かっています。そのため、もし虚数の時間発展と実数の時間発展が同じ性質を示すのであれば、虚数の時間発展で生成される量子もつれ(=有限温度における量子もつれ)の大きさも虚数時間i/(2T)に比例するはずです。この場合、有限温度における量子もつれの境界則は図2で示したように1/T(T-1)に比例して破れることになります。
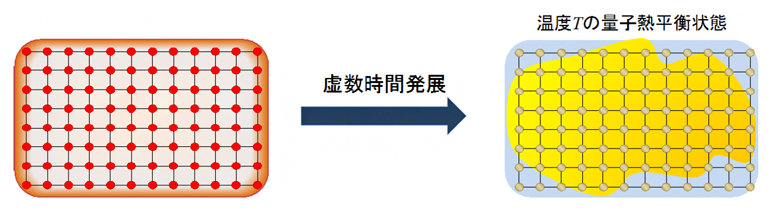
図3 虚数時間発展による量子熱平衡状態の生成
初期状態(左)を一様な分布で用意し、虚数時間i/(2T)だけ時間発展すると、温度Tの量子熱平衡状態となる。このとき、有限温度における量子もつれの大きさは、虚数の時間発展で生成される量子もつれの大きさに等しい。
国際共同研究チームは、近年の計算機科学の成果を用いることで、指数関数exのをxの多項式で表すこと(多項式近似[9])に必要な次数の大きさが、変数xが実数の場合と虚数の場合とで定性的に異なっていることに着目しました。そして、虚数の時間発展による粒子の運動がランダムウォーク[10]とのアナロジー(類似性)を持っていることを解明しました。このアナロジーと量子もつれに関する従来の数学手法を組み合わせることで、虚数の時間発展によって生成される量子もつれの大きさが虚数時間i/(2T)の2/3乗に比例することを明らかにしました。これは、量子もつれの境界則は温度Tの逆数(T-1)に比例して破れるのではなく、温度Tの逆数の2/3乗(T-2/3)に比例して破れていくことを意味しています。
さらにこの結果を用いて、1次元上で定義される量子熱平衡状態をコンピュータ上でシミュレートするのに必要な計算時間を明らかにしました。これまでは、粒子数Nのべき乗に比例する時間(Nα[α>1])が必要である(多項式時間アルゴリズム[11])と考えられていましたが、Nにほぼ比例する時間で計算する計算手法(擬線形時間のアルゴリズム[12])を新たに開発しました。
以上の結果は、基礎的には有限温度における量子もつれの大きさ、虚数の時間発展による量子もつれの生成量に関する従来の予想を覆しました。また、量子熱平衡状態のシミュレーション時間が従来よりも大幅に短縮できることも示されました。
今後の期待
本研究を通して、有限温度における量子もつれの普遍法則、またシミュレーションに必要な計算時間が明らかになりました。今後は、1次元を超える一般の次元の量子熱平衡状態をより効率的に取り扱う手法の開発、特にテンソルネットワーク[13]を用いて量子熱平衡状態を近似する際に、どの程度のメモリが必要になるのかを解明していくことを目指しています。
これらの理解は今後、量子コンピューティング、量子機械学習などの具体的な計算手法の効率化に大きく貢献すると期待できます。
補足説明
1.量子多体系
量子力学に従って互いに相互作用する多数粒子系のこと。
2.有限温度
絶対零度(0ケルビン、約-273℃)でも無限大でもない一定の温度のこと。
3.量子もつれ
異なる粒子間に現れる量子力学特有の相関。
4.虚数の時間発展
シュレディンガー方程式において、時間を虚数にしたときに波動関数の変化を表したもの。
5.量子シミュレーション
量子コンピュータ上で、量子力学の原理を用いて、対象となる物質や現象をシミュレートすること。
6.量子機械学習
量子コンピュータを用いて機械学習の問題を効率的に解くこと。一部の問題は量子コンピュータによって超高速化が達成できることが知られている。
7.量子熱平衡状態
一定の温度を保つ、時間とともに変化しない安定な量子状態。
8.もつれの大きさ
量子もつれの大きさを定量的に特徴づけるためのさまざまな量が提案されているが、本研究ではエンタングルメント・オブ・ピュリフィケーションと呼ばれる量を用いている。
9.多項式近似
ある複雑な関数を、有限次の多項式を用いて近似すること。
10.ランダムウォーク
粒子がある位置から別の位置に動く際に、どの位置に動くのかが確率的に決定されるような運動のこと。
11.多項式時間アルゴリズム
ある問題を解く際に、インプットの大きさN(例えば、粒子数)に対して、計算時間がNの冪乗(例えば、N2やN3)で増大するような計算手法。
12.擬線形時間のアルゴリズム
ある問題を解く際に、インプットの大きさN(例えば、粒子数)に対して、計算時間がほぼ比例して増大するような計算手法。
13.テンソルネットワーク
複雑な量子状態を効率的に計算するための数学的な記述方法。
国際共同研究チーム
理化学研究所 革新知能統合研究センター
汎用基盤技術研究グループ 数理科学チーム
研究員 桑原 知剛(くわはら ともたか)
マックス・プランク研究所
研究員 アルバーロ・アルハンブラ(Alvaro M. Alhambra)
カリフォルニア大学バークレー校
研究員 アヌラーク・アンシュ(Anurag Anshu)
研究支援
本研究は、日本学術振興会(JSPS)科学研究費補助金若手研究「テンソルネットワーク形式を用いた量子多体問題の計算複雑性解析(研究代表者:桑原知剛)」の支援のもとに行われました。
原論文情報
Tomotaka Kuwahara, álvaro M. Alhambra, Anurag Anshu, “Improved thermal area law and quasi-linear time algorithm for quantum Gibbs states”, Physical Review X
発表者
理化学研究所
革新知能統合研究センター 汎用基盤技術研究グループ 数理科学チーム
研究員 桑原 知剛(くわはら ともたか)
報道担当
理化学研究所 広報室 報道担当