2025-12-24 シカゴ大学
<関連情報>
- https://news.uchicago.edu/story/why-cant-powerful-ais-learn-basic-multiplication
- https://arxiv.org/abs/2510.00184
- https://arxiv.org/pdf/2510.00184
トランスフォーマーはなぜ掛け算を学習できないのか?リバースエンジニアリングで長距離依存関係の落とし穴が明らかに Why Can’t Transformers Learn Multiplication? Reverse-Engineering Reveals Long-Range Dependency Pitfalls
Xiaoyan Bai, Itamar Pres, Yuntian Deng, Chenhao Tan, Stuart Shieber, Fernanda Viégas, Martin Wattenberg, Andrew Lee
arXiv Submitted on 30 Sep 2025
DOI:https://doi.org/10.48550/arXiv.2510.00184
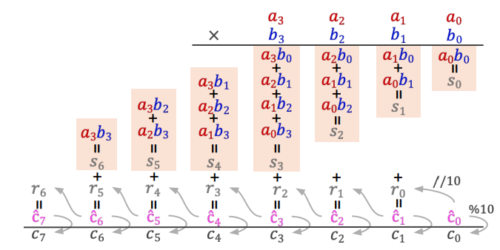
Abstract
Language models are increasingly capable, yet still fail at a seemingly simple task of multi-digit multiplication. In this work, we study why, by reverse-engineering a model that successfully learns multiplication via \emph{implicit chain-of-thought}, and report three findings: (1) Evidence of long-range structure: Logit attributions and linear probes indicate that the model encodes the necessary long-range dependencies for multi-digit multiplication. (2) Mechanism: the model encodes long-range dependencies using attention to construct a directed acyclic graph to “cache” and “retrieve” pairwise partial products. (3) Geometry: the model implements partial products in attention heads by forming Minkowski sums between pairs of digits, and digits are represented using a Fourier basis, both of which are intuitive and efficient representations that the standard fine-tuning model lacks. With these insights, we revisit the learning dynamics of standard fine-tuning and find that the model converges to a local optimum that lacks the required long-range dependencies. We further validate this understanding by introducing an auxiliary loss that predicts the “running sum” via a linear regression probe, which provides an inductive bias that enables the model to successfully learn multi-digit multiplication. In summary, by reverse-engineering the mechanisms of an implicit chain-of-thought model we uncover a pitfall for learning long-range dependencies in Transformers and provide an example of how the correct inductive bias can address this issue.