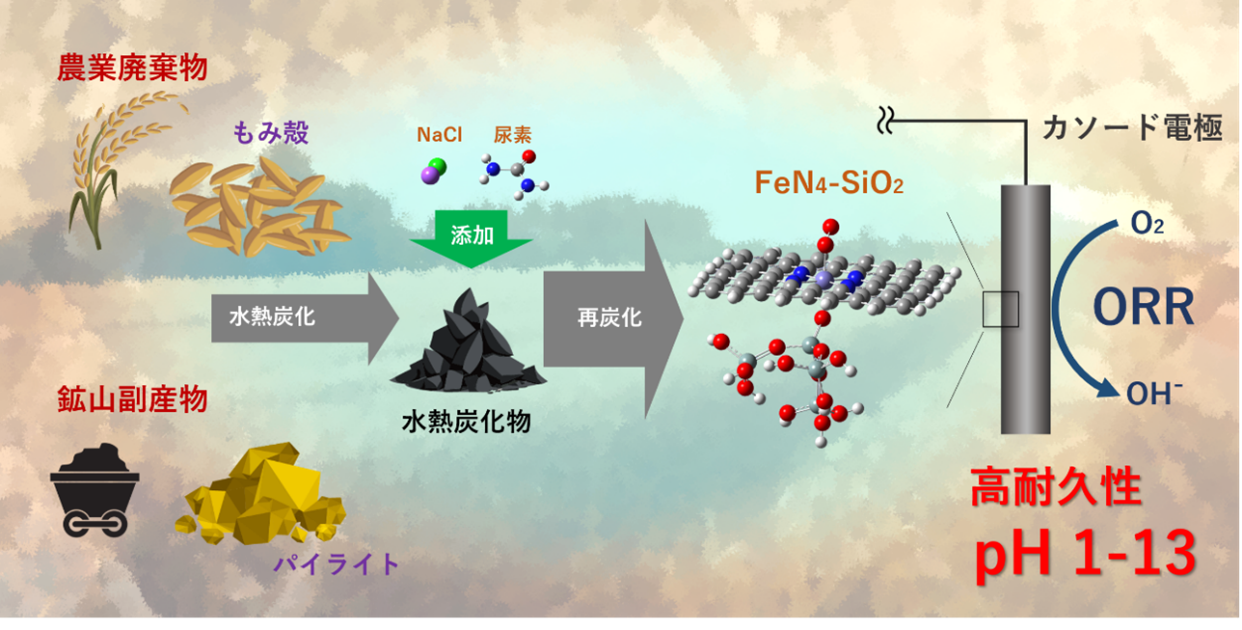
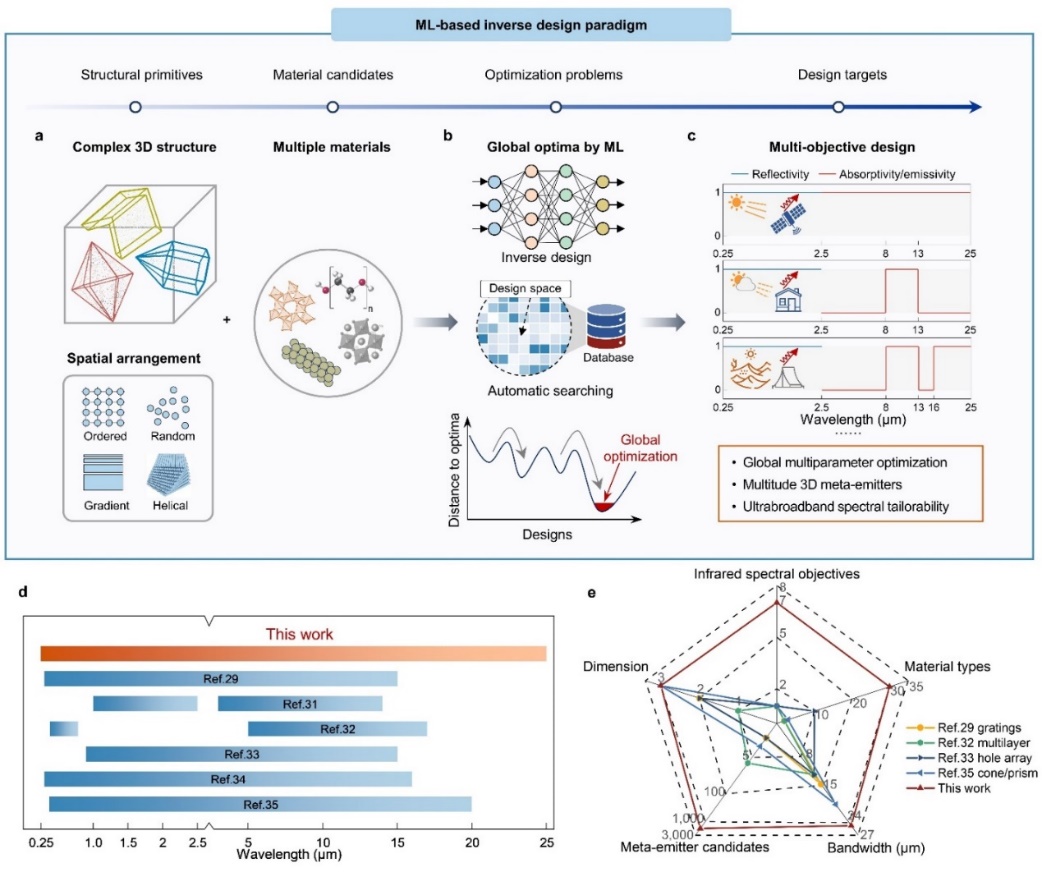
2025-07-03 京都大学
<関連情報>
- https://www.kyoto-u.ac.jp/ja/research-news/2025-07-03
- https://www.kyoto-u.ac.jp/sites/default/files/2025-07/web_2507_Umeno-03da69db6246334d34c3de9381318025.pdf
- https://pubs.aip.org/aip/cha/article/35/7/073108/3351238/Anosov-properties-of-a-symplectic-map-with-time
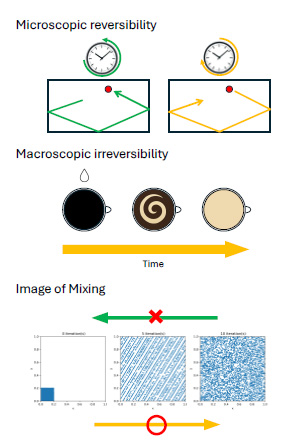
時間反転対称性を持つシンプレクティック写像のアノソフ特性
Anosov properties of a symplectic map with time-reversal symmetry
Ken-ichi Okubo;Ken Umeno
Chaos Published:July 01 2025
DOI:https://doi.org/10.1063/5.0248135
This study presents a specific symplectic map, derived from a Hamiltonian, as a model that exhibits time-reversal symmetry on a microscopic scale. Based on the analysis, any initial density function, defined almost everywhere, converges to a uniform distribution in terms of mixing (irreversible behavior) on a macroscopic level. Furthermore, we established that this mixing invariant measure is a unique equilibrium state, unique Sinai–Ruelle–Bowen measure, and physical measure. Additionally, through analytical proof, we have shown that the Kolmogorov–Sinai entropy representing the average information gain per unit time is positive. This was achieved by validating Pesin’s formula and demonstrating that the critical exponent of the Lyapunov exponent is 1/2.