2023-06-19 理化学研究所,名古屋大学
理化学研究所(理研)計算科学研究センター データ同化研究チームの三好 建正 チームリーダー(開拓研究本部 三好予測科学研究室 主任研究員、数理創造プログラム 副プログラムディレクター)、キウェン・ソン 大学院生リサーチ・アソシエイト(研究当時)、名古屋大学のセルジュ・リシャール 教授の共同研究チームは、低次元の理想実験により、極端な大雨や高温などの極端現象の発生を防ぐ制御可能性を明らかにしました。
本研究成果は、激甚化しつつある台風や豪雨を制御し、極端風水害の脅威を軽減するための理論研究の発展に貢献すると期待できます。
今回、共同研究チームは、簡単なカオス力学系として知られるローレンツ40変数モデル[1]を使って、制御シミュレーション実験(Control Simulation Experiment;CSE)を実行し、当該モデルにおける極端現象の発生を防ぐ制御可能性を明らかにしました。ローレンツ40変数モデルは、地球上の緯度が一定の円上に40個の点を並べ、その各点上の気象、例えば気圧や気温、風速、降水などを模したものと考えられます。それぞれの点での値は、刻々と上下に変動します。この値が1年に2度の割合で大きな値を示す極端現象に対し、微小な制御入力[2]を与えることで、この極端現象の発生を防ぐことに成功しました。今後、ローレンツ40変数モデルの代わりに実際の気象モデルを使うことで、極端な大雨や高温などの極端気象の制御可能性研究への扉が開かれます。
本研究は、科学雑誌『Nonlinear Processes in Geophysics』オンライン版(6月19日付:日本時間6月19日)に掲載され、6月18~22日にイタリア・ローマで開催される第3回国際非線形動力学会議(NODYCON2023)の冒頭のキーノート講演(6月19日)にて発表されました。
背景
気候変動が進み、過去に経験しなかったような激しい気象が発生するようになってきました。極端な大雨や高温などの極端気象は、時に命を脅かします。これに対応するには、極端気象の発生を事前に予測し、備えることが重要です。一方、極端気象の発生自体を防ぐ制御ができれば、気象災害リスクを大幅に減らすことができます。このように極端気象を制御し、気象災害の脅威から解放された社会を2050年に実現したい社会像として掲げ、三好建正チームリーダーらは2021年1月から半年間、ムーンショット型研究開発事業新たな目標検討のためのビジョン策定(ミレニア・プログラム)の課題「気象制御可能性に関する調査研究」に取り組みました。
この成果として、2022年3月28日に「制御シミュレーション実験―気象制御に向けた新理論―」を発表しました注1)。その際、ローレンツ3変数モデル[3]を使い、当該モデルのレジーム[4]遷移を防ぐ制御可能性を明らかにしました。ここで考案した制御シミュレーション実験(Control Simulation Experiment;CSE)は、予測を難しくするカオス的性質[5]を逆手に取り、人為的にわずかな変化を繰り返し与えることで、狙った方向に大きく変化させる効率的な制御の可能性を調べる方法で、ローレンツ3変数モデルだけではなく、さまざまなモデルに適用可能な一般理論です。
大規模で複雑な気象モデルは、計算量やデータ量が膨大となります。このため、気象予測の新しい方法を切り拓く基礎的な理論研究では、さまざまなアイデアを試行錯誤する必要があり、計算量やデータ量が非常に小さい低次元の数理モデルがしばしば使われます。ローレンツ3変数モデルはその代表的なものですが、最も単純な部類に含まれます。その次の段階として代表的なものに、ローレンツ40変数モデルがあります。ローレンツ40変数モデルのそれぞれの変数は、時に大きな値を取り、それは大雨や高温に対応した極端現象と考えることができます。いつ極端現象が起こるかは、モデルのカオス的性質のため、予測可能性に限界があります。
本研究では、このローレンツ40変数モデルを使って、極端現象の発生を防ぐCSEを実施し、制御可能性について研究しました。
注1)2022年3月28日プレスリリース「制御シミュレーション実験」
研究手法と成果
共同研究チームはまず、ローレンツ40変数モデルを実装し、6時間ごと、100年分の時系列データを作成して、ヒストグラムを作りました(図1白)。次に、このヒストグラムから、1年に2回の頻度で発生する極端値の閾値(境界となる値)を求めました(図1赤)。その後、この時系列データを真の状態と仮定し、ノイズを加えて観測データとしました。ここでは、真の状態は完全には知り得ないものとし、不完全な観測を行うためにノイズを加えました。そして、この観測データを使ったデータ同化[6]によって、真の状態を推定する観測システムシミュレーション実験(OSSE)[7]を行いました。データ同化手法の一つであるアンサンブルカルマンフィルタ[8]を適用したところ、10個のアンサンブルによって精度よく真の状態を推定できることを確認しました。
次に、CSEを設計しました(図2)。上記のOSSEの10個のアンサンブルを使った予報のうち、1個以上が閾値を超える極端値を予報した場合に(図2上)、制御入力を与え真の状態を変化させることにしました(図2下)。CSEの制御入力の大きさや範囲などを変えることで、制御可能性を調べることができます。
ローレンツ40変数モデルでは極端値の発生が予測対象となるため、制御対象として1年に2回の頻度で発生する極端値を選び、制御入力により極端値の発生を防ぐことを狙いました。その結果、観測データのノイズの大きさと比べてわずか4%の大きさの制御入力により、極端値の発生を大幅に軽減する制御可能性が明らかになりました(図1青)。
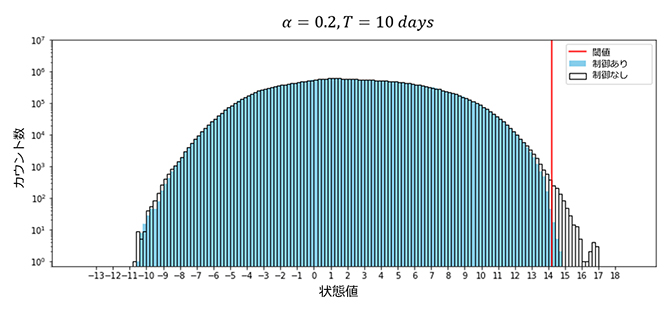
図1 ローレンツ40変数モデルの6時間ごとの値の100年分のヒストグラム
縦軸はカウント数、横軸は変数の取る値を表す。
白:制御入力がない場合のヒストグラムを示す。
赤:制御入力がない場合に1年に2回の頻度で発生する極端値の閾値を示す。
青:制御入力がある場合のヒストグラムを示す。
赤で示される閾値を超える極端値について、青と白の分布を比較すると、制御入力によって極端値の発生が大幅に減っている。
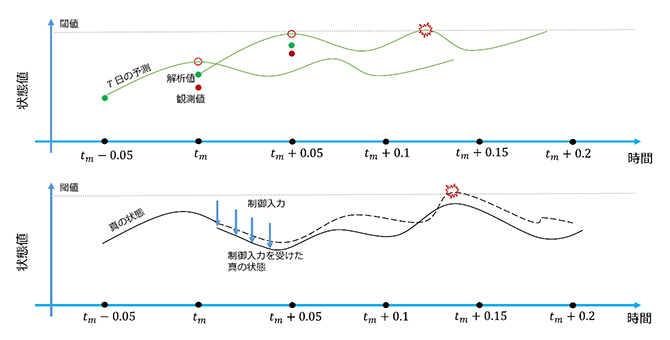
図2 極端現象を防ぐ制御シミュレーション実験
縦軸は変数の取る値、横軸は時刻を表す。
上:時刻tmを初期時刻とした予報(緑線)が、極端値の閾値(灰色点線)を超えている(赤爆発)。
下:時刻tm以降の真の状態(黒破線)が、制御入力(青下向き矢印)によって変化し(黒実線)、極端値の発生(赤爆発)を防ぐことができた。
今後の期待
本研究は、ローレンツ40変数モデルを使うことで、CSEによる極端値の発生を防ぐ制御を切り開き、制御可能性を明らかにしました。今後、ローレンツ40変数モデルの代わりに実際の気象モデルを使うことで、豪雨や突風、高温など気象の極端値の発生を防ぐ制御可能性研究への扉が開かれると期待できます。
補足説明
1.ローレンツ40変数モデル
1996年欧州中期天気予報センター(ECMWF)の予測可能性に関するセミナーでの講演「Predictability – A problem partly solved」の中で、エドワード・N・ローレンツ博士が用いた40変数のカオス力学系モデル。
2.制御入力
制御を行うために与える入力。
3.ローレンツ3変数モデル
1963年アメリカ気象学会の科学雑誌『Journal of Atmospheric Sciences』に発表した論文「Deterministic Nonperiodic Flow」の中で、エドワード・N・ローレンツ博士が用いた3変数のカオス力学系モデル。
4.レジーム、レジーム遷移
レジームとは状態や体制を意味する。異なるレジーム間の移動をレジーム遷移(レジーム・シフト)という。
5.カオス的性質
わずかな違いが後の大きな違いを引き起こす性質のことで、1匹の蝶の羽ばたきが数日先の嵐を引き起こす例えから「バタフライ効果」としても知られる。
6.データ同化
シミュレーション結果を、実際の観測結果と突き合わせて修正する手法。シミュレーションで作られた世界は、そのままでは現実世界とかけ離れていくので、実際の観測結果と突き合わせて修正する。
7.観測システムシミュレーション実験(OSSE)
仮想の観測システムをシミュレーションし、数値天気予報における有効性を評価する仮想シミュレーション実験。OSSEはObserving Systems Simulation Experimentの略。
8.アンサンブルカルマンフィルタ
アンサンブルとは、フランス語で「一緒に」「ひとそろい、全体」という意味で、複数のシミュレーションを実行して、同等に確からしい「パラレルワールド」を作り、予測のばらつきを表現する。例えば、3個のアンサンブル予報では、3個の独立なシミュレーションを並行して実行する。アンサンブルの数が増えるほど統計上のランダム誤差が減少するが、必要な計算能力も格段に増加する。アンサンブルカルマンフィルタは、複数のシミュレーションによるアンサンブル予報を用いて、日々変動する誤差を考慮する高度なデータ同化手法で、数値天気予報の標準的手法の一つ。
研究支援
本研究は、科学技術振興機構(JST)ムーンショット型研究開発事業新たな目標検討のためのビジョン策定(ミレニア・プログラム)の課題「気象制御可能性に関する調査研究」および理研の大学院生リサーチ・アソシエイト制度の支援を受けて行われました。
原論文情報
Qiwen Sun, Takemasa Miyoshi and Serge Richard, “Control simulation experiments of extreme events with the Lorenz-96 model”, Nonlinear Processes of Geophysics, 10.5194/npg-30-117-2023
発表者
理化学研究所
計算科学研究センター データ同化研究チーム
チームリーダー 三好 建正(ミヨシ・タケマサ)
(開拓研究本部 三好予測科学研究室 主任研究員、数理創造プログラム 副プログラムディレクター)
大学院生リサーチ・アソシエイト(研究当時)キウェン・ソン(Qiwen Sun)
名古屋大学
教授 セルジュ・リシャール(Serge Richard)
報道担当
理化学研究所 広報室 報道担当
東海国立大学機構 名古屋大学広報課