2024-12-09 アメリカ合衆国・ジョンズ・ホプキンズ大学
<関連情報>
- https://hub.jhu.edu/2024/12/09/trayanova-engineering-artificial-intelligence/
- https://www.nature.com/articles/s43588-024-00732-2
偏微分方程式の形状依存解演算子を学習するスケーラブルなフレームワーク A scalable framework for learning the geometry-dependent solution operators of partial differential equations
Minglang Yin,Nicolas Charon,Ryan Brody,Lu Lu,Natalia Trayanova & Mauro Maggioni
Nature Computational Science Published:09 December 2024
DOI:https://doi.org/10.1038/s43588-024-00732-2
Abstract
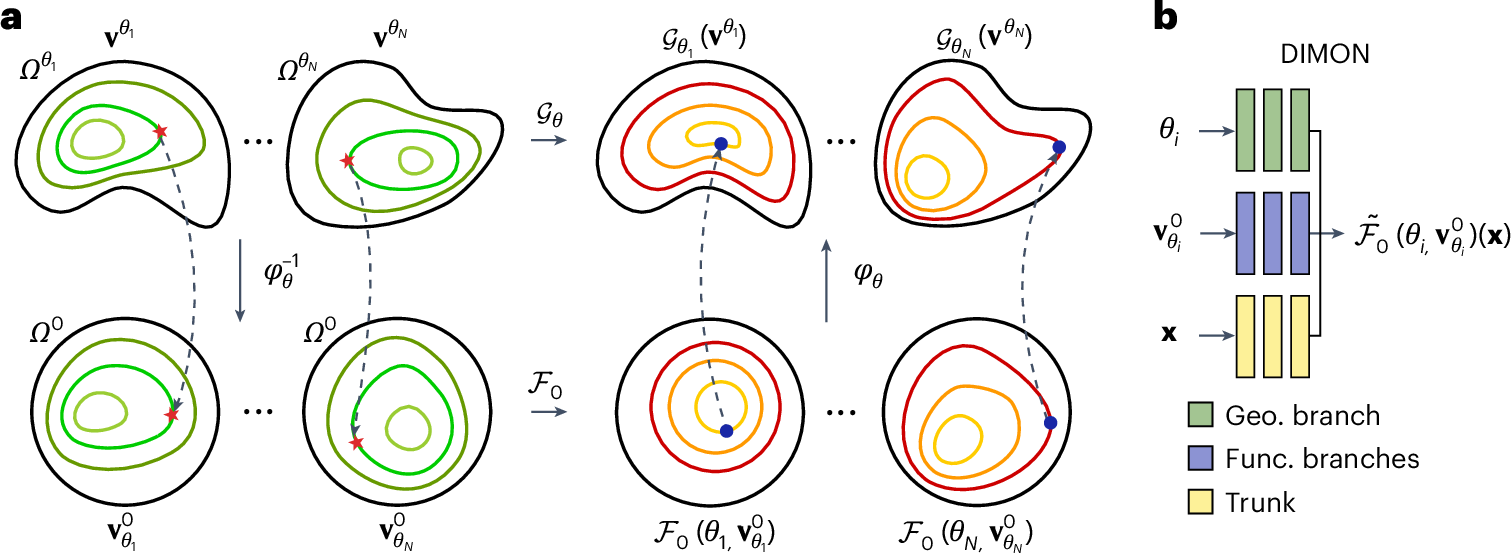
Solving partial differential equations (PDEs) using numerical methods is a ubiquitous task in engineering and medicine. However, the computational costs can be prohibitively high when many-query evaluations of PDE solutions on multiple geometries are needed. Here we aim to address this challenge by introducing Diffeomorphic Mapping Operator Learning (DIMON), a generic artificial intelligence framework that learns geometry-dependent solution operators of different types of PDE on a variety of geometries. We present several examples to demonstrate the performance, efficiency and scalability of the framework in learning both static and time-dependent PDEs on parameterized and non-parameterized domains; these include solving the Laplace equations, reaction–diffusion equations and a system of multiscale PDEs that characterize the electrical propagation on thousands of personalized heart digital twins. DIMON can reduce the computational costs of solution approximations on multiple geometries from hours to seconds with substantially less computational resources.


