2023-07-12 理化学研究所,東京大学,科学技術振興機構
理化学研究所(理研)量子コンピュータ研究センター 光量子計算研究チームの阪口 淳史 特別研究員、古澤 明 チームリーダー(量子コンピュータ研究センタ ー副センター長、東京大学大学院 工学系研究 科教授)らの国際共同研究グループは、量子計算[1]のための光電場の非線形[2]測定を初めて実現しました。
本研究成果は、光を使った量子コンピュータ[1]において汎用的な量子計算を可能にする非線形計算に相当し、誤り耐性型[3]汎用光量子コンピュータの実現につながると期待できます。
非線形測定は光量子コンピュータにおいて「掛け算」を可能にするために不可欠の要素であり、その実現は長年の課題でした。
今回、国際共同研究グループは、デジタル回路を用いた柔軟かつ高速な非線形計算を電気-光制御に導入することで、光電場に対する非線形測定器を構築しました。さまざまな入力光を用意し、入出力関係から測定器の量子的な性質を確認し、作製した測定器が所望の非線形測定を実行していることを実証しました。
本研究は、オンライン科学雑誌『Nature Communications』(7月12日付:日本時間7月12日)に掲載されました。
背景
近年、量子コンピュータの実現に向けた研究が盛んに行われています。量子コンピュータは重ね合わせ[1]や量子もつれ[1]といった量子的な性質を利用することで、従来のコンピュータよりも高速に計算を行えると期待されています。
量子コンピュータを実現するハードウェアとして、超伝導を使った量子コンピュータをはじめさまざまな提案がありますが、光を使った量子コンピュータ(光量子コンピュータ)も有望な候補の一つです。その理由に、光量子コンピュータは室温での動作が可能であること、光の周波数は数百テラヘルツ(THz、1THzは1兆ヘルツ)と非常に高いためクロック周波数[4]を高くでき、計算の高速化が可能であること、既存の光通信との親和性が高いため複数の量子コンピュータ間の連携がしやすいことなどが挙げられます。
これまでの研究で、パルス列状に飛んで来る量子光同士の時間をずらし、複雑に干渉させた量子もつれ状態に対して、測定と測定値に基づく動的な操作(フィードフォワード[5]と呼ばれる)を行うことで、量子状態の変化と補正を行いながら計算する測定型量子計算[6]の手法が開発されました。この方法の利点は、同一のセットアップを各時間のパルスごとに使い回すことができ、セットアップの空間的な規模を保ったまま量子コンピュータの大規模化が可能という点です。
測定型量子計算では、測定の種類と精度が量子操作の種類と精度に対応しています。しかし、これまで実現されていたのは非線形性のないホモダイン測定[7]に限られていました。ホモダイン測定では決定論的[8]に光電場の加減算・定数倍操作のみが可能ですが、そのような操作は従来の計算機で効率的にシミュレーション可能なことが知られています。しかし任意の量子計算が可能な光量子コンピュータでは光電場同士の「掛け算」操作を行う必要があり、そのためには決定論的な非線形操作に相当する非線形測定が必要不可欠です。
このような非線形測定のうち、最も基礎的な非線形測定を実現するための手法は2001年に提案され、2016年には具体的なセットアップ案も提案されました注1)。その案では、被測定光と補助的な量子光を干渉させ、得られる二つの光の片方にホモダイン測定をし、他方にはその測定結果に非線形計算を行った値に基づき動的に位相回転操作をする、というフィードフォワードの後にホモダイン測定をすることで、非線形測定として働くとされています(図1)。
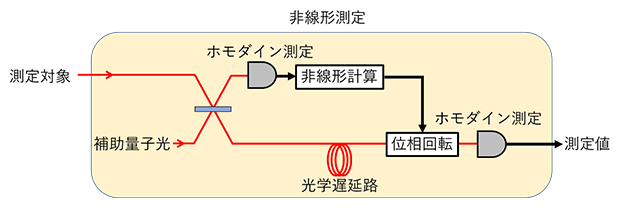
図1 提案された非線形測定のセットアップ
赤が光信号の経路、黒が電気信号の経路。黄色で囲われた部分全体で非線形測定として働く。光学遅延路は非線形計算の遅延に合わせて光信号を遅らせるための装置で、計算が遅いほど長い距離になり、光損失や位相ゆらぎといったデコヒーレンス(量子状態の情報が失われること)の原因となる。
しかし、実際には非線形計算を電気的に行う際にかかる時間が長く、光速で飛び回る光の信号との同期が難しかったことや、補助量子光として必要な非線形スクイーズド光[9]の生成が難しかったことから非線形測定は実現されていませんでした。補助量子光に関しては2021年に近似状態の生成が報告されましたが注2)、非線形なフィードフォワードは未実現のままでした。
注1)K. Miyata et al., Implementation of a quantum cubic gate by an adaptive non-Gaussian measurement. Physical Review A 93, 022301 (2016).
注2)S. Konno et al., Nonlinear Squeezing for Measurement-Based Non-Gaussian Operations in Time Domain. Physical Review Applied 15, 024024 (2021).
研究手法と成果
国際共同研究グループは、電気-光のフィードフォワード制御をデジタル回路により柔軟かつ高速に行う手法を提案し、その手法を用いた制御系と非線形スクイーズド光を組み合わせることで、任意の量子計算を実現する上で不可欠な非線形測定の原理実証に成功しました。提案手法では柔軟な制御が可能なため、別の補助量子光と組み合わせれば誤り耐性型汎用量子計算にも利用できます。
本研究で提案した手法では、フィードフォワード中の測定結果に対する非線形計算を、ルックアップテーブルと呼ばれる計算表を用いて行います。ルックアップテーブルは、プログラマブル[10]なデジタル回路内のメモリブロックを使用して実装されており、事前に入出力の組を書き込んであります。入力の値をメモリのアドレスに、出力の値をメモリに記録する値に対応させることで、計算結果を1クロックサイクル[4](本研究では約2.67ナノ秒[ns、1nsは10億分の1秒])で読み出すことができます。実際の計算は事前に行う必要があるものの、ルックアップテーブルに書き込む計算表を変えれば、計算にかかる時間を保ったまま計算の種類を変えることもできます。
測定系・制御系の入出力信号はアナログ信号で、デジタル回路に入出力するにはデジタル・アナログ間の変換やその他のアナログ回路が必要なため、専用のボードを作製し(図2)、それらを含めた合計の遅延を約26.8nsに抑えています。CPU(中央演算処理装置)などを用いたマイクロ秒(µs、1µsは100万分の1秒)オーダーでの計算と比べて100倍程度の高速化となっています。この柔軟かつ高速な非線形計算により、光学系との同期が容易となったことで、非線形測定が実験的に可能になりました。

図2 非線形計算に使用した専用ボード
必要な電気素子以外の遅延を抑えるため素子の配置にも注意して設計されている。
ただし、実現される非線形測定の精度は、測定対象となる光に干渉させる補助量子光によって制限されるため、非線形スクイーズド光を補助量子光として使用することで、非線形測定の精度を理想的な値に近づける必要があります。本研究では、補助量子光として2021年に生成された近似状態と同様の量子状態を準備し、その有無による変化も観測しました。
構築した実験系の評価として、27通りの強度・ランダムな位相を持つ弱いレーザー光を216万通り測定対象として入力することで、入力した光と測定結果の関係を検証しました。この関係から量子トモグラフィー[11]と呼ばれる計算により、測定器を特徴づける「測定値と対応する量子状態の変化先の組」を推定できます。その結果、測定器の基準位相に対する入力光の同一位相成分[12]については2乗に比例し、直交位相成分[12]については比例する測定値が得られることや、量子状態の変化先のウィグナー関数[13]が理論から予想される形状と近いこと(忠実度[14]での換算では0.99以上)(図3)、さらには補助量子光として非線形スクイーズド光を使用することで測定のノイズが減少し、その減少量が理論値と整合することも確かめられました。これらの結果から、構築した実験系が目標としていた非線形測定となっていることが実証されました。
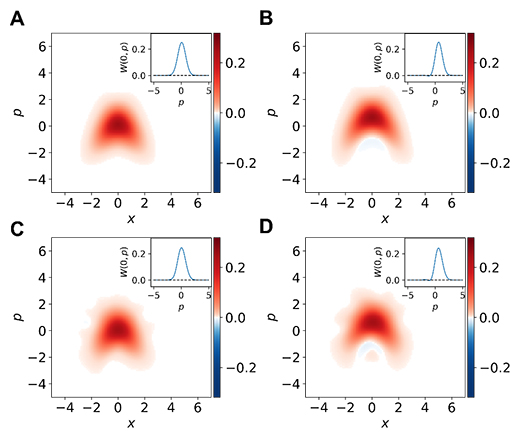
図3 推定された量子状態の変化先のウィグナー関数と理論予想の比較
グラフは、量子状態の変化先のウィグナー関数と呼ばれる、測定器の基準位相に対する入力光の同一位相(in-phase)成分(x)、直交位相(quadrature-phase)成分(p)の擬似的な確率分布を表す。
A)理論的に期待される量子状態の変化先(補助量子光無)。
B)理論的に期待される量子状態の変化先(補助量子光有)。
C)実験から推定された量子状態の変化先(補助量子光無)。
D)実験から推定された量子状態の変化先(補助量子光有)。
いずれも理論と実験で同様の形状をしており、フィードフォワードが正しく動作していることを示している。
今後の期待
本研究では、デジタル回路による柔軟かつ高速な非線形計算の手法を電気-光制御に導入することで非線形なフィードフォワードを可能にし、補助量子光と組み合わせて汎用光量子コンピュータに不可欠な非線形測定の原理実証に成功しました。
補助量子光を高精度化することで非線形測定の精度を高め、また異なる補助量子光と組み合わせて、誤り耐性型汎用光量子計算の実現に貢献すると期待できます。
補足説明
1.量子計算、量子コンピュータ、重ね合わせ、量子もつれ
量子計算は波としての性質・粒としての性質を併せ持つ量子を用いて計算を行うことであり、それを実用化した次世代の計算機が量子コンピュータである。量子の状態は波としての性質から、ある状態を別の波を足し合わせた(重ね合わせ)状態として表現できる。量子もつれ状態とはある種の相関が生じており、別々の独立な状態として表現できない状態のことを呼ぶ。
2.非線形
線形は入出力関係をグラフに書いた場合に直線で表せるような性質であり、非線形性は線形を持たない性質のこと。これまでの研究でフィードフォワードとして使用された計算は、定数倍および足し算(と引き算)により構成される変換が大部分だった。本研究で実証した非線形操作は光電場の2乗を求めることに相当し、これまでに実現された線形操作と組み合わせて光電場の掛け算が実現可能となる。
3.誤り耐性型
計算において誤りがあった場合でもそれを検出して訂正できるような方式のこと。量子計算においては、未知の量子状態を複製することは不可能なため、従来の誤り耐性型計算の手法は使えないが、量子もつれ状態や光のような多準位系を離散化した状態を用いて、同じ量子情報を複数の要素で表す(冗長化する)ことで、一部に誤りがあっても訂正可能になる。本研究で開発されたフィードフォワードは光量子計算の誤り訂正操作に利用できる。
4.クロック周波数、クロックサイクル
一定のタイミングで0と1が繰り返される信号(クロック信号)の1秒当たりの繰り返し回数をクロック周波数と呼ぶ。逆に1回の繰り返しにかかる時間をクロックサイクルと呼ぶ。計算機ではクロック信号の繰り返しごとに計算を行うため、1クロックサイクル当たりの計算能力が同じ場合は、クロック周波数が高いほど速く計算できる。
5.フィードフォワード
測定値に基づいた制御において、制御対象が再び同じ測定を受けない場合のこと。再び同じ測定をされる場合がフィードバックに相当する。特に光では、測定した量子光が測定器に吸収されることがほとんどで、時間的に同じセットアップを使い回す場合でも異なる量子状態として扱うためフィードフォワードと呼ぶ。
6.測定型量子計算
量子状態に対する測定結果は確率分布に従い、ある測定値を得たときには測定された量子状態がその結果に応じて変化する。測定型量子計算では、あらゆる状態の重ね合わせである量子状態に対して、適切な測定を選び、次の測定を繰り返すことで、測定結果に応じて量子状態を変化させ、量子操作を実現する。測定値は確率的で一定の値とは限らないため、異なる測定値でも同じ操作を実現するにはフィードフォワードで測定値ごとの差を補正する必要がある。
7.ホモダイン測定
ローカルオシレーター光と呼ばれる強いレーザー光と測定対象の微弱光を干渉させることで、測定対象の光電場の特定の位相成分信号を増幅して測定する手法。測定対象の電場に比例した電圧信号を高精度に得られる。特に本研究では、ハーフビームスプリッタで干渉させた二つの光の強度差を測定するバランス型ホモダイン測定を用いている。ローカルオシレーター光と測定対象の光の位相によって、位相空間の射影軸を選ぶことができる。
8.決定論的
操作が条件なしに成功すること。逆は確率的。測定型の量子計算において測定値は確率的で一定の値とは限らないが、測定値に応じたフィードフォワードにより補正することで決定論的な操作となる。測定の種類によっては測定結果のばらつきを補正できるフィードフォワードが存在するとは限らず、一定の測定値の場合のみを成功とする確率的な操作しかできないことがある。確率的な操作では操作回数が増えるほど成功の確率が下がるという欠点がある。
9.非線形スクイーズド光
光電場の非線形項の量子ゆらぎが圧搾された(スクイーズド)光の量子状態。図1のような非線形測定では、測定対象の非線形項に補助量子光の非線形項が足されてしまうため、それがノイズとして働く。
10.プログラマブル
特定の指示に従って手順や構成を変更可能であること。本研究ではField Programmable Gate Array(FPGA)と呼ばれる、ハードウェアを記述する言語で書かれた通りに組み替え可能なデジタル回路を用いた。
11.量子トモグラフィー
量子状態とそれに対する測定、測定結果の分布の関係性から量子状態または測定を推定する手法。本研究では入力に対して実際に得た測定結果の分布を得る確率が最も高くなる測定を求めることで推定を行った(最尤推定法)。量子状態を推定する場合は同一の量子状態を何度も生成して既に特性の分かっている測定を行い、測定を推定する場合は特性の分かっている量子状態を同一の測定器に何度も入力する必要がある。
12.同一位相成分、直交位相成分
光を量子化した際に共役となる二つの成分で、消滅演算子の実部・虚部に対応する演算子で表現される。測定器の基準位相に対する入力光の同一位相(in-phase)成分と直交位相(quadrature-phase)成分は、光を調和振動子として見たときの位置と運動量の関係にある。定義には自由度があるが本研究ではホモダイン測定の測定方向を基準として設定している。
13.ウィグナー関数
量子状態を同一位相成分と直交位相成分の擬次的な同時確率分布として表した関数。不確定性原理と呼ばれる原理から二つの成分は同時には決定できず、また量子状態によっては負の値を取るため、確率分布そのものではないが確率分布と似た性質を持つ。例えば、ウィグナー関数を直交位相成分について積分して得られる周辺分布は、量子状態の同一位相成分の測定値の確率分布になっている。
14.忠実度
二つの量子状態の「近さ」を表す尺度の一つ。量子状態が一致するとき1になる。
国際共同研究グループ
理化学研究所 量子コンピュータ研究センター 光量子計算研究チーム
特別研究員 阪口 淳史(サカグチ・アツシ)
研究員 吉川 純一(ヨシカワ・ジュンイチ)
チームリーダー 古澤 明(フルサワ・アキラ)
(理研 量子コンピュータ研究センター 副センター長、東京大学大学院 工学系研究科 教授)
東京大学大学院 工学系研究科 物理工学専攻
助教 アサバナント・ワリット(Asavanant Warit)
助教 高瀬 寛(タカセ・カン)
博士課程学生(研究当時)小川 尚史(オガワ・ヒサシ)
博士課程学生(研究当時)紺野 峻也(コンノ・シュンヤ)
博士課程学生 花村 文哉(ハナムラ・フミヤ)
パラツキー大学(チェコ)
教授 ラディム・フィリップ(Radim Filip)
准教授 ペトル・マレク(Petr Marek)
オーストラリア国立大学
教授 エレノア・ハンティントン(Elanor Huntington)
ニューサウスウェールズ大学(オーストラリア)
上級講師(研究当時)米澤 英宏(ヨネザワ・ヒデヒロ)
研究支援
本研究は科学技術振興機構(JST)ムーンショット型研究開発事業ムーンショット目標6「2050年までに、経済・産業・安全保障を飛躍的に発展させる誤り耐性型汎用量子コンピュータを実現(プログラムディレクター:北川勝浩)」の研究開発プロジェクト「誤り耐性型大規模汎用光量子コンピュータの研究開発(プロジェクトマネージャー:古澤明)」(JPMJMS2064)の一環として行われました。
原論文情報
Atsushi Sakaguchi, Shunya Konno, Fumiya Hanamura, Warit Asavanant, Kan Takase, Hisashi Ogawa, Petr Marek, Radim Filip, Jun-ichi Yoshikawa, Elanor Huntington, Hidehiro Yonezawa and Akira Furusawa., “Nonlinear feedforward enabling quantum computation”, Nature Communications, 10.1038/s41467-023-39195-w
発表者
理化学研究所
量子コンピュータ研究センター 光量子計算研究チーム
特別研究員 阪口 淳史(サカグチ・アツシ)
チームリーダー 古澤 明(フルサワ・アキラ)
(理研 量子コンピュータ研究センター 副センター長、東京大学 大学院工学系研究科 教授)
報道担当
理化学研究所 広報室 報道担当
東京大学 大学院工学系研究科 広報室
科学技術振興機構 広報課
JST事業に関すること
科学技術振興機構 ムーンショット型研究開発事業部
櫻間 宣行(サクラマ・ノリユキ)