数理解析により、崩壊しにくい渦構造を発見 Mathematical analysis identifies a vortex structure that is impervious to decay
2022-12-12 フィンランド・アールト大学
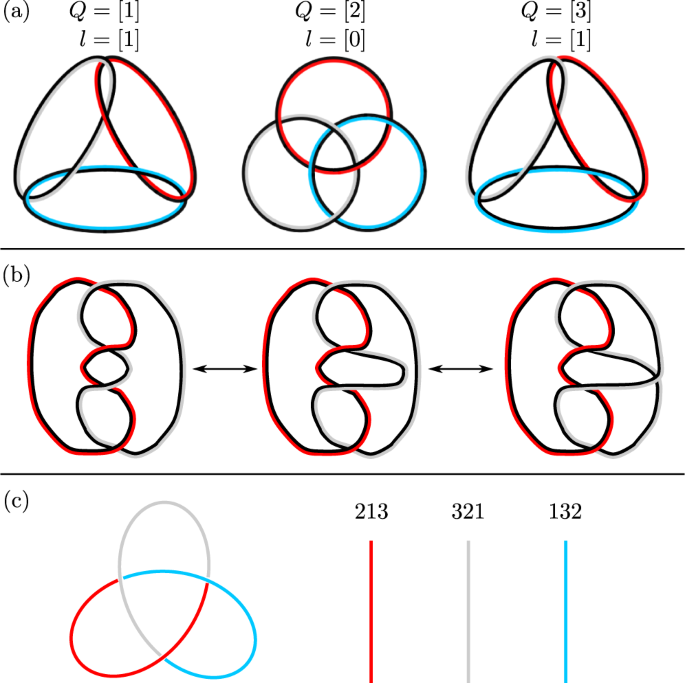
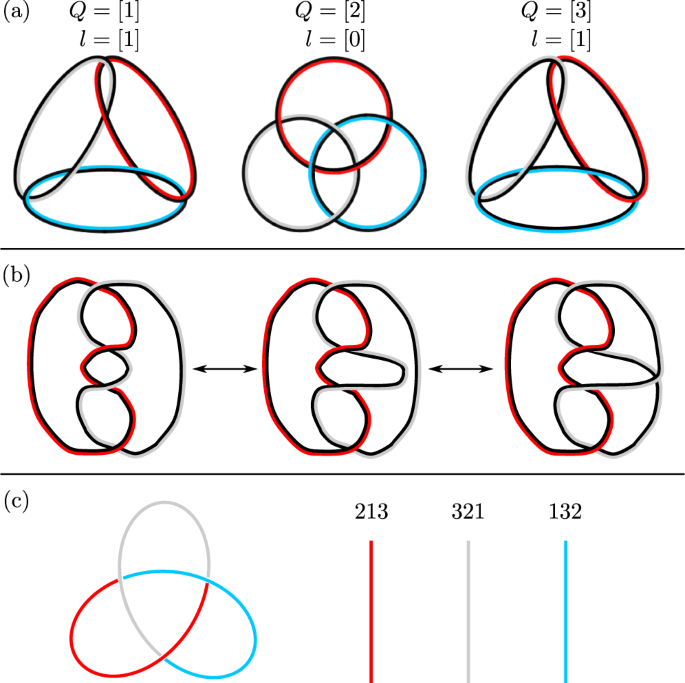
研究者らは、基本的な性質からバラバラにならない渦がつながった構造が存在することを数学的に証明した。ここでの新しい要素は、トポロジー的な影響を受けることなく、つながっていながら互いに通り抜けることができない3つの異なる流れの渦を、数学的に構築できたということです。もし渦が互いに入り込めば、その交点に紐ができ、渦が結合してエネルギーを消費する。つまり、この構造は簡単には壊れないのです」とメトローネン教授は言う。
この構造は、象徴主義や紋章に広く用いられてきた3つの円が連なったパターンであるボロメア環と概念的に類似している。オーディンに関連するバイキングのシンボルは、3つの三角形が同じように組み合わされている。円や三角形の1つを取り除くと、残りの2つは直接接続されないため、パターン全体が溶解する。このように、各要素は相手となる2つの要素を結びつけ、全体として構造を安定させるのである。
今回の数学的解析により、結び目でつながった渦の間にも、同じような安定した構造が存在することが明らかになった。このような構造は、ある種の液晶や凝縮系で観察される可能性があり、それらの系の挙動や発展の仕方に影響を与える可能性がある。
研究者らは次に、実験的に実現可能なシナリオとして、ボーズ-アインシュタイン凝縮において、トポロジカルに溶解しないように保護された結び目が存在することを理論的に実証する予定である。「トポロジカルに保護された結び目の存在は、自然界の基本的な問題の1つです。数学的な証明がなされれば、シミュレーションや実験的な研究に進むことができます」とMöttönen教授は語っている。
<関連情報>
- https://www.aalto.fi/en/news/a-peculiar-protected-structure-links-viking-knots-with-quantum-vortices
- https://www.nature.com/articles/s42005-022-01071-2
位相的に保護された渦巻き状の結び目とリンク Topologically protected vortex knots and links
Toni Annala,Roberto Zamora-Zamora & Mikko Möttönen
Communications Physics Published:12 December 2022
DOI:https://doi.org/10.1038/s42005-022-01071-2
Abstract
In 1869, Lord Kelvin found that the way vortices are knotted and linked in an ideal fluid remains unchanged in evolution, and consequently hypothesized atoms to be knotted vortices in a ubiquitous ether, different knotting types corresponding to different types of atoms. Even though Kelvin’s atomic theory turned out incorrect, it inspired several important developments, such as the mathematical theory of knots and the investigation of knotted structures that naturally arise in physics. However, in previous studies, knotted and linked structures have been found to untie via local cut-and-paste events referred to as reconnections. Here, in contrast, we construct knots and links of non-Abelian vortices that are topologically protected in the sense that they cannot be dissolved employing local reconnections and strand crossings. Importantly, the topologically protected links are supported by a variety of physical systems such as dilute Bose-Einstein condensates and liquid crystals. We also propose a classification scheme for topological vortex links, in which two structures are considered equivalent if they differ from each other by a sequence of topologically allowed reconnections and strand crossings, in addition to the typical continuous transformations. Interestingly, this scheme produces a remarkably simple classification.