2026-01-15 理化学研究所
<関連情報>
- https://www.riken.jp/press/2026/20260115_1/index.html
- https://link.springer.com/article/10.1007/s11071-025-12021-2
カオスシステムの双対性原理:データ同化から効率的な制御まで A duality principle for chaotic systems: from data assimilation to efficient control
Takemasa Miyoshi
Nonlinear Dynamics Published:14 January 2026
DOI:https://doi.org/10.1007/s11071-025-12021-2
Abstract
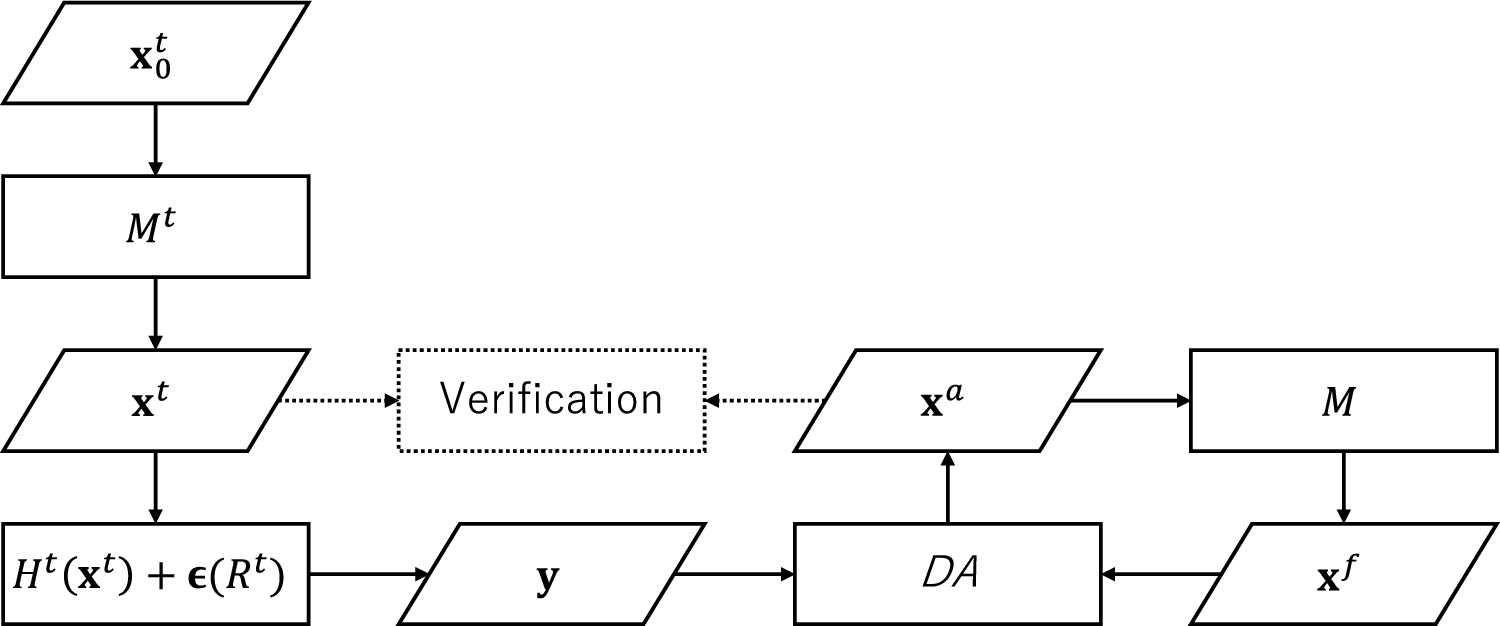
E. N. Lorenz discovered the highly sensitive nature of a chaotic dynamical system and conveyed it vividly by his famous “butterfly effect”; namely, a flap of a butterfly could cause a storm a few days later somewhere far away. Extreme weather like intense storms tends to be more chaotic and harder to predict, with increasing threat due to climate change. This motivates us to ask if we could possibly modify extreme weather in a favorable manner by taking advantage of its strong chaoticity. Here, the problem is that the causality from a flap of a butterfly to a storm formation is not trivial due to the limited predictability. Due to chaos, a small perturbation grows exponentially and leads to a different future state, but the difference becomes large enough only after the predictable range. This paper addresses this apparent paradox by presenting the first rigorous mathematical formalization of the Control Simulation Experiment (CSE) framework, an extension of the data assimilation (DA) paradigm. We then propose a duality principle based on chaos synchronization: while DA uses observations to synchronize a model to nature’s trajectory, we argue that control uses interventions to synchronize nature to a chosen target trajectory. The feasibility of this control rests on the key insight that these target trajectories can be selected to have distinct dynamical properties from the original system, reframing the challenge from taming a fully chaotic system to maintaining synchronization with a more manageable path.