可逆なシステムにおいて時間の矢を持つのは何故か～ある時間反転対称性を持つ系からアナソフ性の証明へ～

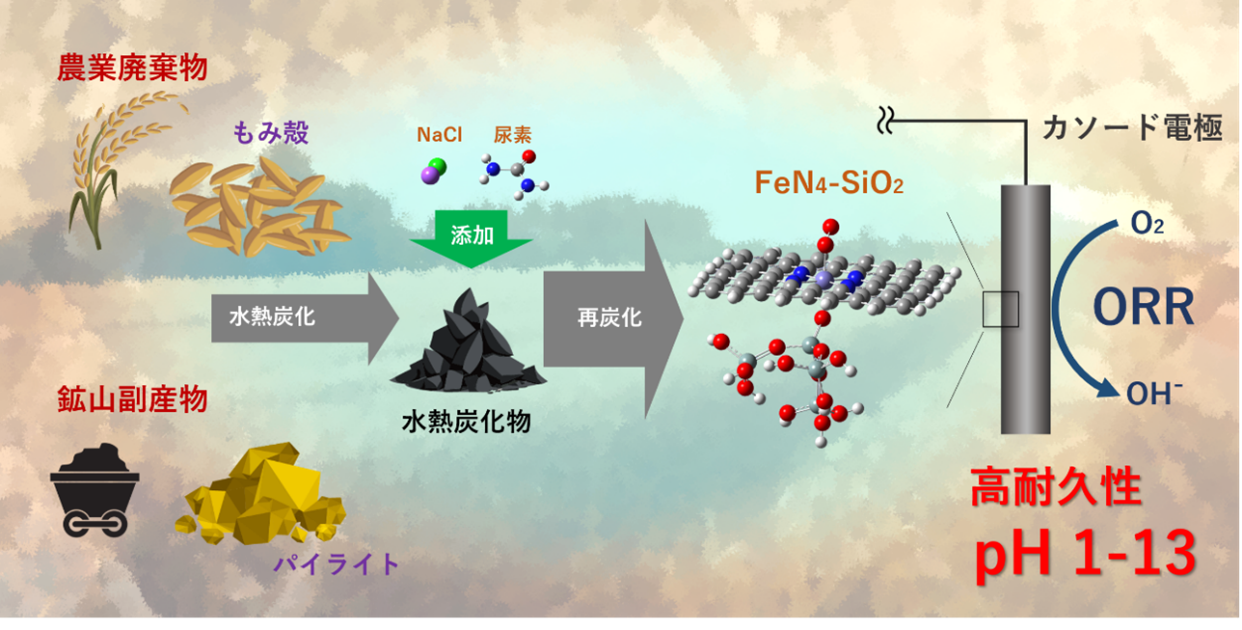
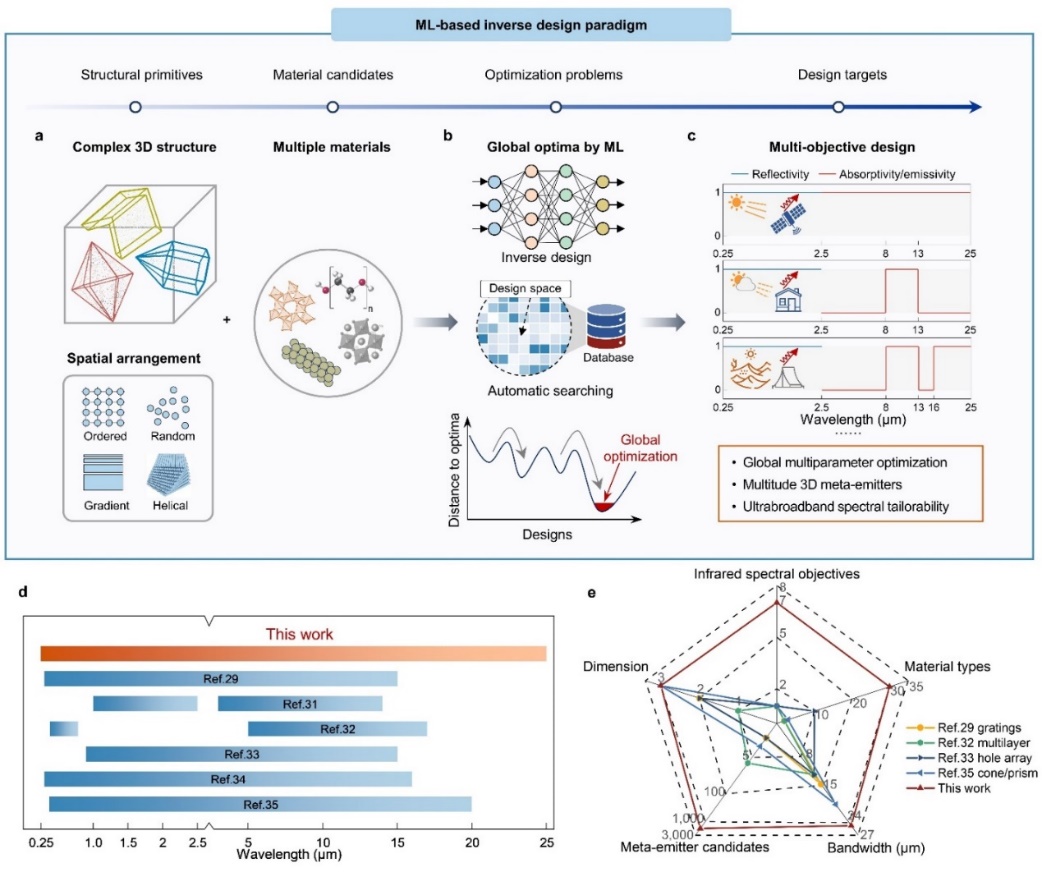
2025-07-03 京都大学

可逆な時間反転対称性を持つ力学系でも「時間の矢（不可逆性）」が現れる理由について、梅野健教授らの研究グループは、初めて具体的な物理モデルにより証明した。リープフロッグ法という時間反転対称性を保持する数値積分法を用いて構成したモデルから、唯一の平衡状態に収束するアナソフ性（カオス性）を持つことを数学的に示した。これは、時間反転対称なミクロな運動法則から、マクロな不可逆性（熱力学第二法則）が自然に現れることの証明であり、AIや次世代カオス・サンプリングへの応用も期待される。

＜関連情報＞

時間反転対称性を持つシンプレクティック写像のアノソフ特性
Anosov properties of a symplectic map with time-reversal symmetry

Ken-ichi Okubo;Ken Umeno
Chaos Published:July 01 2025
DOI:https://doi.org/10.1063/5.0248135

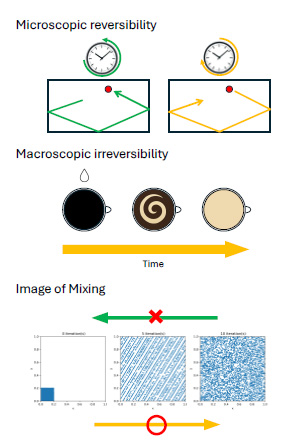
This study presents a specific symplectic map, derived from a Hamiltonian, as a model that exhibits time-reversal symmetry on a microscopic scale. Based on the analysis, any initial density function, defined almost everywhere, converges to a uniform distribution in terms of mixing (irreversible behavior) on a macroscopic level. Furthermore, we established that this mixing invariant measure is a unique equilibrium state, unique Sinai–Ruelle–Bowen measure, and physical measure. Additionally, through analytical proof, we have shown that the Kolmogorov–Sinai entropy representing the average information gain per unit time is positive. This was achieved by validating Pesin’s formula and demonstrating that the critical exponent of the Lyapunov exponent is 1/2⁠.