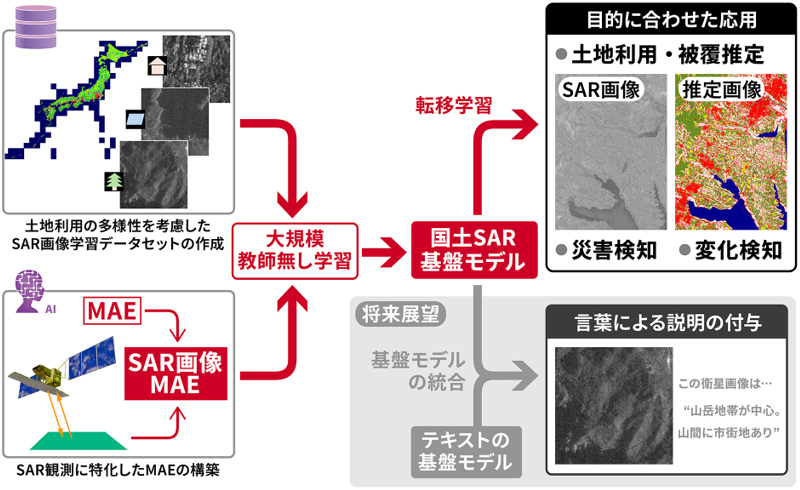
2025-06-02 理化学研究所,東京大学,筑波大学
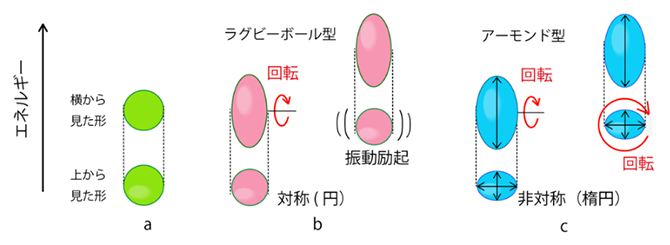
従来のラグビーボール型の原子核(b)と本研究成果のアーモンド型の原子核(c)
<関連情報>
- https://www.riken.jp/press/2025/20250602_1/index.html
- https://link.springer.com/article/10.1140/epja/s10050-025-01553-1
原子核における優勢な三軸形状と複合物体の回転の量子論 Prevailing triaxial shapes in atomic nuclei and a quantum theory of rotation of composite objects
T. Otsuka,Y. Tsunoda,N. Shimizu,Y. Utsuno,T. Abe & H. Ueno
European Physical Journal A Published:02 June 2025
DOI:https://doi.org/10.1140/epja/s10050-025-01553-1
Abstract
Virtually any object can rotate: the rotation of a rod or a linear molecule appears evident, but a number of objects, including a simple example of H2O molecule, are of complex shapes and their rotation is of great interest. For atomic nuclei, rotational bands have been observed in many nuclei, and their basic picture is considered to have been established in the 1950s. We, however, show that there may be substantial changes in the basic picture of nuclear rotation: In the traditional view, as stressed by Aage Bohr in his Nobel lecture with an example of 166Er nucleus, a large fraction of heavy (mass number A>150) nuclei are like axially-symmetric prolate ellipsoids (i.e., with two shorter axes of equal length), rotating about one of the short axes, like a rod. In an alternative picture, however, the lengths of these three axes are all different, called triaxial. The triaxial shape yields more complex rotations. This alternative picture was also discussed in the past, but has not been recognized as a major picture. We show that substantially triaxial shapes occur in a large number of heavy deformed nuclei. Such prevailing triaxiality results in salient descriptions of experimental data over many nuclei, as confirmed by state-of-the-art Configuration Interaction calculations. Two origins are suggested for the triaxiality in the heavy deformed nuclei: (i) binding-energy gain by the symmetry restoration for triaxial shapes, and (ii) another gain by specific components of the nuclear force, like tensor force and high-multipole (e.g. hexadecupole) central force. While the origin (i) produces small triaxiality for virtually all deformed nuclei, the origin (ii) produces medium triaxiality for a certain class of nuclei. An example of the former is 154Sm, a typical showcase of axial symmetry but is now suggested to depict a small yet finite triaxiality. The medium triaxiality is discussed from various viewpoints for some exemplified nuclei including 166Er, and experimental findings, for instance, those by multiple Coulomb excitations decades ago, are re-evaluated to be supportive of the medium triaxiality. Many-body structures of the γ band and the double-γ band are clarified, and the puzzles over them are solved. The well-known J(J + 1) − K2 formula of rotational excitation energies, which was derived by Taylor expansion in the past, is derived in an alternative way with polynomial property, including the previous work as an approximation. The rotational states of strongly and triaxially deformed heavy nuclei are described within quantum many-body framework, with K quantum number shown to be practically conserved. Thus, two long-standing open problems for strongly deformed heavy nuclei, (i) occurrence and origins of triaxial shapes and (ii) quantum many-body description of their rotational bands classified by K quantum number are solved. The picture of prevailing triaxial shapes thus emerges, where the empirically known rotational-band pattern appears with good K quantum number, but the internal structure is different from conventional picture à la A. Bohr. As a feasible experimental approach to the triaxiality of the 0+ ground state, the Relativistic Heavy-Ion Collision is mentioned. Davydov’s claim of triaxial shapes over many nuclei and the validity of his rigid-triaxial-rotor model are separately assessed with high appreciation of the former.